алгебра 7 класс

Филиал Муниципального автономного общеобразовательного учреждения
«Аромашевская средняя общеобразовательная школа имени Героя Советского Союза В.Д. Кармацкого»
Юрминская средняя общеобразовательная школа
Приложение
к основной образовательной программе
основного общего образования
МАОУ «Аромашевская СОШ
им.В.Д.Кармацкого»
Рабочая программа
по алгебре
7 класс
(ФГОС)
с. Юрминка, 2018 г.
1. Пояснительная записка
Рабочая программа учебного курса по алгебре для 7 класса разработана на основе Федерального закона от 29.12.2012г. №273-ФЗ «Об образовании в Российской Федерации»,
ФГОС ООО утв. Приказом Министерства образования и науки Российской Федерации от 17.12.2010 г. №1897, изменения утв. Приказом Министерства образования и науки Российской Федерации от 29.12.2014 г., примерной основной образовательной программы ООО (утв. 2015г.), основной образовательной программы основного общего образования филиал
МАОУ "Аромашевская средняя общеобразовательная школа имени В.Д. Кармацкого" Юрминская СОШ (03.06.2015 №60) и авторской программы по алгебре Ю. Н. Макарычева
входящей в сборник рабочих программ «Программы общеобразовательных учреждений: Алгебра, 7 класса», составитель: Т.А. Бурмистрова «Программы общеобразовательных
учреждений: Алгебра , 7 класса».- М. Просвещение, 2013. Планирование ориентировано на учебник «Алгебра 7 класс» под редакцией С.А. Теляковского, авторы: Ю.Н.Макарычев,
Н.Г. Миндюк, К.И. Нешков, С.Б.Суворова, Издательство: М., «Просвещение», 2012 -2014 годы.
Цели
Изучение алгебры в 7 классах направлено на достижение следующих целей:
 овладение системой математических знаний и умений, необходимых для применения в практической деятельности, изучения смежных дисциплин, продолжения образования;
 интеллектуальное развитие, формирование качеств личности, необходимых человеку для полноценной жизни в современном обществе: ясность и точность мысли, критичность мышления, интуиция, логическое мышление, элементы алгоритмической культуры, пространственных представлений, способность к преодолению трудностей;
 формирование представлений об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов;
 воспитание культуры личности, отношения к математике как к части общечеловеческой культуры, понимание значимости математики для научно-технического прогресса.
Основные развивающие и воспитательные цели
Развитие:
 Ясности и точности мысли, критичности мышления, интуиции, логического мышления, элементов алгоритмической культуры, пространственных представлений, способности к преодолению трудностей;
 Математической речи;
 Сенсорной сферы; двигательной моторики;
 Внимания; памяти;
 Навыков само и взаимопроверки.
 Формирование представлений об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов.
Воспитание:
 Культуры личности, отношения к математике как к части общечеловеческой культуры, понимание значимости математики для научно-технического прогресса;
 Волевых качеств;
 Коммуникабельности;
 Ответственности.
Задачи учебного предмета:
Математическое образование в основной школе складывается из следующих содержательных компонентов (точные названия блоков):арифметика; алгебра; геометрия;
элементы комбинаторики, теории вероятностей, статистики и логики. В своей совокупности они отражают богатый опыт обучения математике в нашей стране, учитывают
современные тенденции отечественной и зарубежной школы и позволяют реализовать поставленные перед школьным образованием цели на информационно емком и практически
значимом материале. Эти содержательные компоненты, развиваясь на протяжении всех лет обучения, естественным образом переплетаются и взаимодействуют в учебных курсах.
2
С учетом требований Федерального государственного образовательного стандарта основного общего образования проектирование, организация и оценка результатов образования осуществляется на основе системно - деятельностного подхода, который обеспечивает:
 формирование готовности обучающихся к саморазвитию и непрерывному образованию;
 проектирование и конструирование развивающей образовательной среды образовательного учреждения;
 активную учебно-познавательную деятельность обучающихся;
 построение образовательного процесса с учетом индивидуальных, возрастных, психологических, физиологических, особенностей здоровья обучающихся.
В ходе преподавания алгебры в 7 классах, работы над формированием у учащихся перечисленных в программе знаний и умений, следует обращать внимание на то, чтобы они овладевали умениями общеучебного характера, разнообразными способами деятельности, приобретали опыт: планирования и осуществления алгоритмической деятельности, выполнения заданных и конструирования новых алгоритмов; решения разнообразных классов задач из различных разделов курса, в том числе задач, требующих поиска пути и способов решения; исследовательской деятельности, развития идей, проведения экспериментов, обобщения, постановки и формулирования новых задач; ясного, точного, грамотного изложения
своих мыслей в устной и письменной речи, использования различных языков математики (словесного, символического, графического), свободного перехода с одного языка на другой
для иллюстрации, интерпретации, аргументации и доказательства; проведения доказательных рассуждений, аргументации, выдвижения гипотез и их обоснования; поиска, систематизации, анализа и классификации информации, использования разнообразных информационных источников, включая учебную и справочную литературу, современные информационные технологии.
В курсе алгебры можно выделить следующие основные содержательные линии: арифметика; алгебра; функции; вероятность и статистика.
Содержание линии «Арифметика» служит базой для дальнейшего изучения учащимися математики, способствует развитию их логического мышления, формированию умения
пользоваться алгоритмами, а также приобретению практических навыков, необходимых в повседневной жизни. Развитие понятия о числе в основной школе связано с рациональными и иррациональными числами, формированием первичных представлений о действительном числе.
Содержание линии «Алгебра» способствует формированию у учащихся математического аппарата для решения задач из разделов математики, смежных предметов и окружающей реальности. Язык алгебры подчёркивает значение математики как языка для построения математических моделей процессов и явлений реального мира.
Развитие алгоритмического мышления, необходимого, в частности, для освоения курса информатики, и овладение навыками дедуктивных рассуждений также являются задачами
изучения алгебры. Преобразование символьных форм вносит специфический вклад в развитие воображения учащихся, их способностей к математическому творчеству. В основной
школе материал группируется вокруг рациональных выражений.
Содержание раздела «Функции» нацелено на получение школьниками конкретных знаний о функции как важнейшей математической модели для описания и исследования разнообразных процессов. Изучение этого материала способствует развитию у учащихся умения использовать различные языки математики (словесный, символический, графический),
вносит вклад в формирование представлений о роли математики в развитии цивилизации и культуры.
Раздел «Вероятность и статистика» — обязательный компонент школьного образования, усиливающий его прикладное и практическое значение. Этот материал необходим,
прежде всего, для формирования у учащихся функциональной грамотности — умения воспринимать и критически анализировать информацию, представленную в различных формах, понимать вероятностный характер многих реальных зависимостей, производить простейшие вероятностные расчёты. Изучение основ комбинаторики позволит учащемуся осуществлять рассмотрение случаев, перебор и подсчёт числа вариантов, в том числе в простейших прикладных задачах.
При изучении статистики и вероятности обогащаются представления о современной картине мира и методах его исследования, формируется понимание роли статистики как источника социально значимой информации и закладываются основы вероятностного мышления.
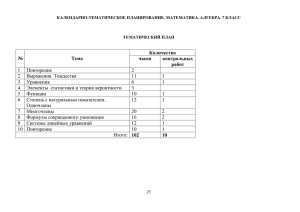
Данная программа рассчитана на 102 ч, предусмотренных в Федеральном базисном (образовательном) учебном плане для образовательных учреждений. Обязательное изучение алгебры осуществляется в объёме: в 7 классе -3 часа в неделю (102 часа в год). В год предусмотрено 9 контрольных работ и 1 итоговая контрольная работа за курс 7 класса.
Формы промежуточной и итоговой аттестации: Промежуточная аттестация проводится в форме тестов, контрольных работ. Итоговая аттестация предусмотрена в виде административной контрольной работы.
2. Планируемые результаты изучения математики
Программа позволяет добиваться следующих результатов освоения образовательной программы основного общего образования:
3
личностные:
1) сформированность ответственного отношения к учению, готовность и способности обучающихся к саморазвитию и самообразованию на основе мотивации к обучению и познанию, выбору дальнейшего образования на базе ориентировки в мире профессий и профессиональных предпочтений, осознанному построению индивидуальной образовательной
траектории с учётом устойчивых познавательных интересов;
2) сформированность целостного мировоззрения, соответствующего современному уровню развития науки и общественной практики;
3) сформированность коммуникативной компетентности в общении и сотрудничестве со сверстниками, старшими и младшими, в образовательной, общественно полезной, учебноисследовательской, творческой и других видах деятельности;
4) умение ясно, точно, грамотно излагать свои мысли в устной и письменной речи, понимать смысл поставленной задачи, выстраивать аргументацию, приводить примеры и
контрпримеры;
5) представление о математической науке как сфере человеческой деятельности, об этапах её развития, о её значимости для развития цивилизации;
6) критичность мышления, умение распознавать логически некорректные высказывания, отличать гипотезу от факта;
7) креативность мышления, инициатива, находчивость, активность при решении алгебраических задач;
8) умение контролировать процесс и результат учебной математической деятельности;
9) способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений.
метапредметные:
1) умение самостоятельно планировать альтернативные пути достижения целей, осознанно выбирать наиболее эффективные способы решения учебных и познавательных задач;
2) умение осуществлять контроль по результату и по способу действия на уровне произвольного внимания и вносить необходимые коррективы;
3) умение адекватно оценивать правильность или ошибочность выполнения учебной задачи, её объективную трудность и собственные возможности её решения;
4) осознанное владение логическими действиями определения понятий, обобщения, установления аналогий, классификации на основе самостоятельного выбора оснований и критериев, установления родовидовых связей;
5) умение устанавливать причинно-следственные связи; строить логическое рассуждение, умозаключение (индуктивное, дедуктивное и по аналогии) и выводы;
6) умение создавать, применять и преобразовывать знаково- символические средства, модели и схемы для решения учебных и познавательных задач;
7) умение организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками: определять цели, распределение функций и ролей участников, взаимодействие и общие способы работы; умение работать в группе: находить общее решение и разрешать конфликты на основе согласования позиций и учёта интересов; слушать
партнёра; формулировать, аргументировать и отстаивать своё мнение;
8) сформированность учебной и общепользовательской компетентности в области использования информационно-коммуникационных технологий (ИКТ - компетентности);
9) первоначальные представления об идеях и о методах математики как об универсальном языке науки и техники, о средстве моделирования явлений и процессов;
10) умение видеть математическую задачу в контексте проблемной ситуации в других дисциплинах, в окружающей жизни;
11) умение находить в различных источниках информацию, необходимую для решения математических проблем, и представлять её в понятной форме; принимать решение в условиях неполной и избыточной, точной и вероятностной информации;
12) умение понимать и использовать математические средства наглядности (рисунки, чертежи, схемы и др.) для иллюстрации, интерпретации, аргументации;
13) умение выдвигать гипотезы при решении учебных задач и понимать необходимость их проверки;
14) умение применять индуктивные и дедуктивные способы рассуждений, видеть различные стратегии решения задач;
15) понимание сущности алгоритмических предписаний и умение действовать в соответствии с предложенным алгоритмом;
16) умение самостоятельно ставить цели, выбирать и создавать алгоритмы для решения учебных математических проблем;
17) умение планировать и осуществлять деятельность, направленную на решение задач исследовательского характера.
предметные:
4
1) умение работать с математическим текстом (структурирование, извлечение необходимой информации), точно и грамотно выражать свои мысли в устной и письменной речи,
применяя математическую терминологию и символику, использовать различные языки математики (словесный, символический, графический), обосновывать суждения, проводить классификацию, доказывать математические утверждения;
2) владение базовым понятийным аппаратом: иметь представление о числе, владение символьным языком алгебры, знание элементарных функциональных зависимостей, формирование представлений о статистических закономерностях в реальном мире и о различных способах их изучения, об особенностях выводов и прогнозов, носящих вероятностный
характер;
3) умение выполнять алгебраические преобразования рациональных выражений, применять их для решения учебных математических задач и задач, возникающих в смежных
учебных предметах;
4) умение пользоваться математическими формулами и самостоятельно составлять формулы зависимостей между величинами на основе обобщения частных случаев и эксперимента;
5) умение решать линейные уравнения и неравенства, а также приводимые к ним уравнения, неравенства, системы; применять графические представления для решения и исследования уравнений, неравенств, систем; применять полученные умения для решения задач из математики, смежных предметов, практики;
6) овладение системой функциональных понятий, функциональным языком и символикой, умение строить графики функций, описывать их свойства, использовать функциональнографические представления для описания и анализа математических задач и реальных зависимостей;
7) овладение основными способами представления и анализа статистических данных;
8) умение применять изученные понятия, результаты и методы при решении задач из различных разделов курса, в том числе задач, не сводящихся к непосредственному применению известных алгоритмов.
В результате изучения алгебры ученик должен
знать/понимать

существо понятия математического доказательства; примеры доказательств;

существо понятия алгоритма; примеры алгоритмов;

как используются математические формулы, уравнения; примеры их применения для решения математических и практических задач;

как математически определенные функции могут описывать реальные зависимости; приводить примеры такого описания;

смысл идеализации, позволяющей решать задачи реальной действительности математическими методами, примеры ошибок, возникающих при идеализации;

формулы сокращенного умножения;
уметь

составлять буквенные выражения и формулы по условиям задач; осуществлять в выражениях и формулах числовые подстановки и выполнять соответствующие вычисления, осуществлять подстановку одного выражения в другое; выражать из формул одну переменную через остальные;

выполнять основные действия со степенями с натуральными показателями, с одночленами и многочленами; выполнять разложение многочленов на множители; сокращать алгебраические дроби;

решать линейные уравнения и уравнения, сводящиеся к ним, системы двух линейных уравнений с двумя переменными;

решать текстовые задачи алгебраическим методом, интерпретировать полученный результат, проводить отбор решений, исходя из формулировки задачи;

определять координаты точки плоскости, строить точки с заданными координатами, строить графики линейных функций и функции у=х 2;

находить значения функции, заданной формулой, таблицей, графиком по ее аргументу; находить значение аргумента по значению функции, заданной графиком или
таблицей;

определять свойства функции по ее графику; применять графические представления при решении уравнений и систем;

описывать свойства изученных функций, строить их графики;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
5

выполнения расчетов по формулам, составления формул, выражающих зависимости между реальными величинами; нахождения нужной формулы в справочных ма-
териалах;

моделирования практических ситуаций и исследования построенных моделей с использованием аппарата алгебры;

описания зависимостей между физическими величинами соответствующими формулами при исследовании несложных практических ситуаций;

интерпретации графиков реальных зависимостей между величинами.
В результате изучения элементов логики, комбинаторики, статистики и теории вероятностей ученик должен:
уметь
· проводить несложные доказательства, получать простейшие следствия из известных или ранее полученных утверждений, оценивать логическую правильность рассуждений, использовать примеры для иллюстрации и контрпримеры для опровержения утверждений;
· извлекать информацию, представленную в таблицах, на диаграммах, графиках; составлять таблицы, строить диаграммы и графики;
· решать комбинаторные задачи путем систематического перебора возможных вариантов, а также с использованием правила умножения;
· вычислять средние значения результатов измерений;
· находить частоту события, используя собственные наблюдения и готовые статистические данные;
· находить вероятности случайных событий в простейших случаях;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
· выстраивания аргументации при доказательстве (в форме монолога и диалога);
· распознавания логически некорректных рассуждений;
· записи математических утверждений, доказательств;
· анализа реальных числовых данных, представленных в виде диаграмм, графиков, таблиц;
· решения практических задач в повседневной и профессиональной деятельности с использованием действий с числами, процентов, длин, площадей, объемов, времени, скорости;
· решения учебных и практических задач, требующих систематического перебора вариантов;
· сравнения шансов наступления случайных событий, оценки вероятности случайного события в практике.
3. Содержание учебного курса
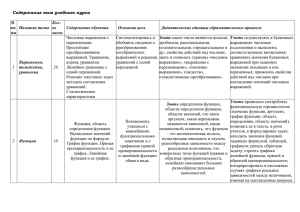
1. Выражения и их преобразования. Уравнения.22ч.
Числовые выражения и выражения с переменными. Простейшие преобразования выражений. Уравнение с одним неизвестным и его корень, линейное уравнение. Решение задач
методом уравнений.
Цель - систематизировать и обобщить сведения о преобразовании выражений и решении уравнений с одним неизвестным, полученные учащимися в курсе математики 5,6 классов.
Знать - какие числа являются целыми, дробными, рациональными, положительными, отрицательными и др.; свойства действий над числами; знать и понимать термины «числовое
выражение», «выражение с переменными», «значение выражения», тождество, «тождественные преобразования».
Уметь - осуществлять в буквенных выражениях числовые подстановки и выполнять соответствующие вычисления; сравнивать значения буквенных выражений при заданных значениях входящих в них переменных; применять свойства действий над числами при нахождении значений числовых выражений.
Статистические характеристики.
Цель - понимать практический смысл статистических характеристик.
Знать - простейшие статистические характеристики.
Уметь - в несложных случаях находить эти характеристики для ряда числовых данных.
2. Функции.11ч.
Функция, область определения функции, Способы задания функции. График функции. Функция у=кх+Ьи её график. Функция у=кх и её график.
6
Цель - познакомить учащихся с основными функциональными понятиями и с графиками функций у=кх+Ь, у=кх.
Знать - определения функции, области определения функции, области значений, что такое аргумент, какая переменная называется зависимой, какая независимой; понимать, что
функция - это математическая модель, позволяющая описывать и изучать разнообразные зависимости между реальными величинами, что конкретные типы функций (прямая и обратная пропорциональности, линейная) описывают большое разнообразие реальных зависимостей.
Уметь - правильно употреблять функциональную терминологию (значение функции, аргумент, график функции, область определение, область значений), понимать ее в тексте, в речи
учителя, в формулировке задач; находить значения функций, заданных формулой, таблицей, графиком; решать обратную задачу; строить графики линейной функции, прямой и обратной пропорциональности; интерпретировать в несложных случаях графики реальных зависимостей между величинами, отвечая на поставленные вопросы
3. Степень с натуральным показателем. 11ч.
Степень с натуральным показателем и её свойства. Одночлен. Функции у=х2, у=х3, и их графики.
Цель - выработать умение выполнять действия над степенями с натуральными показателями.
Знать - определение степени, одночлена, многочлена; свойства степени с натуральным показателем, свойства функций у=х 2 , у=х3 .
Уметь - находить значения функций, заданных формулой, таблицей, графиком; решать обратную задачу; строить графики функций у=х 2, у=х3; выполнять действия со степенями с
натуральным показателем; преобразовывать выражения, содержащие степени с натуральным показателем; приводить одночлен к стандартному виду.
4. Многочлены. 17ч.
Многочлен. Сложение, вычитание и умножение многочленов. Разложение многочлена на множители.
Цель - выработать умение выполнять сложение, вычитание, умножение многочленов и разложение многочленов на множители.
Знать - определение многочлена, понимать формулировку заданий: «упростить выражение», «разложить на множители».
Уметь - приводить многочлен к стандартному виду, выполнять действия с одночленом и многочленом; выполнять разложение многочлена вынесением общего множителя за скобки;
умножать многочлен на многочлен, раскладывать многочлен на множители способом группировки, доказывать тождества.
5. Формулы сокращённого умножения. 19ч.
Формулы(a±b) = a2 ±2ab+b2, (a-b)(a + b) = а2–b2 ,[{a±b)(a2+ab+b2)].Применение формул сокращённого умножения к разложению на множители.
Цель - выработать умение применять в несложных случаях формулы сокращённого умножения для преобразования целых выражений в многочлены и для разложения многочленов
на множители.
Знать - формулы сокращенного умножения: квадратов суммы и разности двух выражений; различные способы разложения многочленов на множители.
Уметь - читать формулы сокращенного умножения, выполнять преобразование выражений применением формул сокращенного умножения: квадрата суммы и разности двух выражение, умножения разности двух выражений на их сумму; выполнять разложение разности квадратов двух выражений на множители; применять различные способы разложения многочленов на множители; преобразовывать целые выражения; применять преобразование целых выражений при решении задач.
6. Системы линейных уравнений16ч.
Система уравнений с двумя переменными. Решение систем двух линейных уравнений с двумя переменными. Решение задач методом составления систем уравнений.
Цель- познакомить учащихся со способами решения систем линейных уравнений с двумя переменными, выработать умение решать системы уравнений и применять их при решении
текстовых задач.
Знать - что такое линейное уравнение с двумя переменными, система уравнений, знать различные способы решения систем уравнений с двумя переменными: способ подстановки,
способ сложения; понимать, что уравнение - это математический аппарат решения разнообразных задач из математики, смежных областей знаний, практики.
Уметь - правильно употреблять термины: «уравнение с двумя переменными», «система»; понимать их в тексте, в речи учителя, понимать формулировку задачи «решить систему
уравнений с двумя переменными»; строить некоторые графики уравнения с двумя переменными; решать системы уравнений с двумя переменными различными способами.
7. Повторение. Решение задач. 6ч.
Закрепление знаний, умений и навыков, полученных на уроках по данным темам (курс алгебры 7 класса).
Формы организации учебного процесса

индивидуальные,
7
 групповые,
 индивидуально-групповые,
 фронтальные
В системе уроков выделяются следующие виды:
 Урок-лекция. Предполагаются совместные усилия учителя и учеников для решения общей проблемной познавательной задачи. На таком уроке используется демонстрационный материал на компьютере, разработанный учителем или учениками, мультимедийные продукты.
 Урок-практикум. На уроке учащиеся работают над различными заданиями в зависимости от своей подготовленности. Виды работ могут быть самыми разными: письменные
исследования, решение различных задач, практическое применение различных методов решения задач, интерактивные уроки. Компьютер на таких уроках используется как
электронный калькулятор, тренажер устного счета, виртуальная лаборатория, источник справочной информации.
 Урок-исследование. На уроке учащиеся решают проблемную задачу исследовательского характера аналитическим методом и с помощью компьютера с использованием различных лабораторий.
 Комбинированный урок предполагает выполнение работ и заданий разного вида.
 Урок–игра. На основе игровой деятельности учащиеся познают новое, закрепляют изученное, отрабатывают различные учебные навыки.
 Урок решения задач. Вырабатываются у обучающихся умения и навыки решения задач на уровне базовой и продвинутой подготовке. Любой учащийся может использовать
компьютерную информационную базу по методам решения различных задач, по свойствам элементарных функций и т.д.
 Урок-тест. Тестирование проводится с целью диагностики пробелов знаний, контроля уровня обученности, тренировки технике тестирования. Тесты предлагаются как в
печатном, так и в электронном варианте. Причем в компьютерном варианте всегда с ограничением времени.
 Урок-зачет. Устный и письменный опрос обучающихся по заранее составленным вопросам, а также решение задач разного уровня по изученной теме.
 Урок - самостоятельная работа. Предлагаются разные виды самостоятельных работ.
 Урок - контрольная работа. Проводится на двух уровнях: уровень базовый (обязательной подготовки) - «3», уровень продвинутый - «4» и «5».
Формы и виды контроля



текущий контроль в виде проверочных работ и тестов;
тематический контроль в виде контрольных работ;
итоговый контроль в виде контрольной работы и теста.
4. Тематическое планирование с определением основных видов учебной деятельности
№
п/п
Разделы программы
Тема урока
Глава I. Выражения, тождества, уравнения
§1
Выражения
1
Числовые выражения
2
Выражения с переменными
Количество
часов
22
5
1
2
Характеристика основных видов учебной деятельности обучающихся
Находить значения числовых выражений, а также выражений с переменными при
указанных значениях переменных. Используя знаки ≤, ≥, <, >, читать и составлять
двойные неравенства.
Выполнять простейшие преобразования выражений: приводить подобные слагаемые,
раскрывать скобки в сумме или разности выражений.
8
3
Сравнение значений выражений
2
§2
4
5
Преобразования выражений
Свойства действий над числами
Тождества. Тождественные преобразования выражений
4
2
2
§3
6
7
8
Контрольная работа №1
Уравнения с одной переменной
Уравнение и его корни
Линейное уравнение с одной переменной
Решение задач с помощью уравнений
1
7
1
2
3
§4
9
10
Статистические характеристики
Среднее арифметическое, размах и мода
Медиана как статистическая характеристика
4
2
2
Контрольная работа №2
Глава II. Функции
§5
Функции и их графики
12
Что такое функция
13
Вычисление значений функции по формуле
14
График функции
§6
15
16
Линейная функция
Прямая пропорциональность и ее график
Линейная функция и ее график
Контрольная работа №3
Глава III. Степень с натуральным показателем
Степень и ее свойства
§7
§8
21
22
Определение степени с натуральным показателем
Умножение и деление степеней
Возведение в степень произведения и степени
Одночлены
Одночлен и его стандартный вид
Умножение одночленов. Возведение одночлена в степень
23
Функции у=х² и у= х³ и их графики
18
19
20
Контрольная работа №4
Решать уравнения вид ах = в при различных значениях а и в, а также несложные
уравнения, сводящиеся к ним.
Использовать аппарат уравнений для решения текстовых задач, интерпретировать
результат. Использовать простейшие статистические характеристики (среднее арифметическое, размах, мода, медиана) для анализа ряда данных в несложных ситуациях
1
11
5
1
2
2
5
2
3
Вычислять значения функции, заданное формулой, составлять таблицы значений
функции. По графику функции находить значение функции по известному значению
аргумента и решать обратную задачу. Строить график прямой пропорциональности и
линейной функции, описывать свойства этих функций. Понимать, как влияет как коэффициента к на расположение в координатной плоскости графика функции у = кх,
где к≠0, как зависит от значений к и в взаимное расположение графиков двух функций вида у=кх+в. Интерпретировать графики реальных зависимостей, описываемых
формулами вида у = кх, где к≠0 и у = кх + в
1
11
5
1
2
2
5
1
2
2
1
Вычислять значение выражения а ͫ, где а – произвольное число,m – натуральное число, устно и письменно, а также с помощью калькулятора. Формулировать, записывать
в символической форме и обосновывать свойства степени с натуральным показателем.
Применять свойства степени для преобразования выражений. Выполнять умножение
одночленов и возведение одночлена в степень. Строить график функции у=х² и у= х³.
Решать графически уравнения х²= кх+в, х³= кх+в, где к и в – некоторые числа
9
Глава IV. Многочлены
§9
Сумма и разность многочленов
25
Многочлен и его стандартный вид
26
Сложение и вычитание многочленов
§10
27
28
§11
29
30
Произведение одночлена и многочлена
Умножение одночлена на многочлен
Вынесение общего множителя за скобки
Контрольная работа №5
Произведение многочленов
Произведение многочлена на многочлен
Разложение многочлена на множители способом группировки
Контрольная работа №6
Глава V. Формулы сокращенного умножения
§12
Квадрат суммы и квадрат разности
32
Возведение в квадрат и куб суммы и разности двух выражений
33
Разложение на множители с помощью формул квадрата суммы и
квадрата разности
§13
Разность квадратов. Сумма и разность кубов
34
Умножение разности двух выражений на их сумму
35
Разложение разности квадратов на множители
36
Разложение на множители суммы и разности кубов
§14
37
38
Контрольная работа №7
Преобразование целых выражений
Преобразование целого выражения в многочлен
Применение различных способов для разложения на множители
Контрольная работа №8
Глава VI. Системы линейных уравнений
§15
40
41
42
Линейные уравнения с двумя переменными и их системы
Линейные уравнения с двумя переменными
График линейного уравнения с двумя переменными
Системы линейных уравнений с двумя переменными
§16
Решение систем линейных уравнений
17
3
1
2
6
3
3
1
6
3
3
Записывать многочлен в стандартном виде, определять степень многочлена. Выполнять сложение и вычитание многочленов, умножение одночлена на многочлен и многочлена на многочлен. Выполнять разложение многочлена на множители, используя
вынесение общего множителя за скобки и способ группировки. Применять действия с
многочленами при решении разнообразных задач, в частности при решении текстовых задач с помощью уравнений.
1
19
5
2
3
6
2
2
2
1
6
3
3
Доказывать справедливость формул сокращенного умножения, применять их в преобразовании целых выражений в многочлены, а также для разложения
многочлена на множители. Использовать различные преобразовании целых выражений при решении уравнений, доказательстве тождеств, в задачах на делимость, в вычислении значений некоторых выражений с помощью калькулятора.
1
16
5
1
2
2
10
Определять, является ли пара чисел решением данногоуравнения с двумя
неизвестными. Находить путем перебора целые решения линейногоуравнения с двумя
переменными. Строить график уравнения ах+ву =с, где а≠0 или в≠0. Решать
графичиским способом системы линейных уравнений с двумя переменными.
Применять способ подстановки и способ сложения при решении системы линейных
уравнений с двумя переменными. Решать текстовые задачи , используя в качестве
10
43
44
45
Способ подстановки
Способ сложения
Решение задач с помощью систем уравнений
3
3
4
Контрольная работа №9
Повторение
Итоговый зачет
1
6
1
Итоговая контрольная работа
Работа над ошибками
1
1
математической модели систему линейных уравнений. Интерпретировать результат ,
полученный при решении системы.
Приложение 1
·
Календарно – тематическое планирование
№
урока
1
2-3
Раздел
программы
Тема урока
Элементы
содержания
(НРК)
Глава I. Выражения, тождества, уравнения
§1Выражен Числовые и алгебраические Алгебраические выравыражения
ия
жения
5ч.
Выражения с переменными Выражения с переменными
Сравнения значений
выражений
4-5
6-7
8-9
§2.Преобраз
ования выражений
4ч.
Свойства действий над числами
Тождества. Тождественные
преобразования выражений
Законы арифметических действий.
Тождество. Доказательство тождеств.
Преобразование выражений.
Требования к результатам
(знать/ уметь)
Умение находить значения числовых выражений
Умение ясно, точно излагать свои мысли в письменной и устной
речи, активность при решении задач
Умение находить значения выражений с переменными при указанных значениях переменных
Умение сравнивать числовые выражения, используя знаки <,>,
считать и составлять двойные неравенства
Умение выполнять простейшие преобразования выражений: приводить подобные слагаемые, раскрывать скобки в сумме или разности выражений
Умение выполнять простейшие преобразования выражений: приводить подобные слагаемые, раскрывать скобки в сумме или разности выражений
Формы контроля
Индивидуальный
опрос; работа по карточкам
Проблемные задания,
фронтальный опрос,
решение упражнений
Взаимопроверка в
группах; практикум
Индивидуальные задания на карточках,
тренировочные
упражнения
Взаимопроверка в
парах; работа с текстом
11
11
§3.Уравнени
я с одной
переменной
7ч.
1214
1517
1819
Контроль умений и навыков из уроков с 1-9
Умение ясно и точно излагать свои мысли в письменной речи,
ответственное отношение к учению
Контрольная работа №1
10
§4.Статис
тические
характеристики
Уравнение и его корни
Линейное уравнение с одной переменной
Линейное уравнение с
одной переменной
Умение решать уравнения вида ах = b при различных значениях а
и b, а также несложные уравнения, сводящиеся к ним.
Практикум, фронтальный опрос
Решение задач с помощью
уравнений
Решение текстовых
задач алгебраическим
способом.
Статистические данные.
Умение использовать аппарат уравнений для решения текстовых
задач, интерпретировать результат
Взаимопроверка в
парах; работа по карточкам
Взаимопроверка в
парах; работа по карточкам
Статистические данные
Умение использовать статистические характеристики для анализа
ряда данных в несложных ситуациях
Среднее арифметическое,
размах и мода
Медиана как статистическая характеристика
2021
Умение решать уравнения вида ах = b при различных значениях а
и b, а также несложные уравнения, сводящиеся к ним.
Понимать смысл поставленной задачи, находчивость, активность
при решении задач, приводить примеры
Контрольная работа №2
2425
2627
2829
Умение использовать статистические характеристики для анализа
ряда данных в несложных ситуациях
Контроль умений и навыков из уроков с 10-21
Умение ясно и точно излагать свои мысли в письменной речи,
ответственное отношение к учению
22
2333
23
Индивидуальное решение контрольных
заданий. Контрольная
работа
Взаимопроверка в
парах
Взаимопроверка в
парах; работа по карточкам
Индивидуальное решение контрольных
заданий .Контрольная
работа
Глава II. Функции
§5.Функции
и их графики
5ч.
§6.Линейна
я функция
Что такое функция
Понятие функции
Умение распознавать функцию по графику
Вычисление значений
функции по формуле
Способы задания
функции
Вычислять значения функции, заданной формулой, составлять
таблицы значений функции.
График функции
График функции
Вычислять значения функции, заданной формулой, составлять
таблицы значений функции, строить графики
Прямая пропорциональность и ее график (интегри-
Функция, описывающая прямую пропорци-
Понимать, как влияет знак коэффициента к на расположение в
координатной плоскости графика функции y=kx, где k≠0, как
Работа с опорными
конспектами разда-
12
5ч.
3032
рованный урок с физикой.
Тема: Чтение и построение
графиков движения")
Линейная функция и ее
график
ональную зависимость,
ее график
зависит от значений к и b взаимное расположение графиков двух
функций у=кх+b
точным материалом
Линейная функция и ее
график. Уравнение
прямой, угловой коэффициент прямой.
Умение строить графики линейной функции, описывать свойства
Работа с раздаточным
материалом
Интерпретация графиков прямой пропорциональности и линейной
функции, составление таблицы значений и построение графиков
Умение ясно и точно излагать свои мысли в письменной речи,
ответственное отношение к учению
Индивидуальное решение контрольных
заданий. Контрольная
работа
Вычисление значений выражений вида аn, где а – произвольное
число, n – натуральное число, устно и письменно, а также с помощью калькулятора. Формулировать, записывать в символической
форме и обосновывать свойства степени с натуральным показателем
Применять свойства степени для преобразования выражений
(умножение и деление степеней)
Работа с конспектом с
книгой и наглядными
пособиями по группам
33
Контрольная работа №3
3444
34
Глава III. Степень с натуральным показателем
Определение степени с
натуральным показателем
Степень с натуральным
показателем.
3536
Умножение и деление степеней
3738
Возведение в степень произведения и степени
Свойства степени с
натуральным показателем.
Свойства степени с
натуральным показателем.
39
4041
4243
44
§7.Степень
и ее свойства
5ч
§8.Одночле
ны
5ч.
Применять свойства степени для преобразования выражений (возведение в степень произведения и степени)
Одночлен и его стандартный вид
Одночлен и его стандартный вид
Понятие одночлена, распознавание одночлена
Умножение одночленов.
Возведение одночлена в
степень
Функции у=х² и у= х³ и их
графики
Умножение одночленов. Возведение одночлена в степень
Функции у=х² и у= х³
и их графики
Умножение одночленов. Возведение одночленов в степень
Контрольная работа №4
Строить графики функций
Вычислять степень числа, применение свойст степеней, умножение одночленов и возведение одночленов в степень
Работа с опорными
конспектами раздаточным материалом
Практикум
,индивидуальный
опрос, работа с
наглядными пособиями
Решение упражнений,
составление опорного
конспекта, ответы на
вопросы
Построение алгоритма действия, решение
упражнений
Решение упражнений,
составление опорного
конспекта.
Индивидуальное решение контрольных
заданий Контрольная
13
работа
4561
45
Глава IV. Многочлены
§9.Сумма и
разность
многочленов
3ч.
4647
4850
Умножение одночлена на
многочлен
5153
Вынесение общего множителя за скобки
54
Контрольная работа №5
5557
5860
§11.Произве
дение многочленов
6ч.
Взаимопроверка в
парах; выполнение
упражнений по образцу
Сложение и вычитание
многочленов
Выполнять сложение и вычитание многочленов
Умножение одночлена
на многочлен
Выполнять умножение одночлена на многочлен
Умение контролировать процесс и результат учебной математической деятельности
Составление опорного конспекта, решение задач, работа с
тестом и книгой
Решение качественных задач
Разложение многочлена на множители
Разложение многочлена на множители (вынесение общего множителя за скобки)
Многочлен и его стандартный вид
Сложение и вычитание
многочленов
§10.Произве
дение одночлена и
многочлена
6ч.
Записывать многочлен в стандартном виде, определять степень
многочлена
Произведение многочлена
на многочлен
Разложение многочлена на
множители способом группировки
Выполнять сложение и вычитание многочленов, выносить общий
множитель за скобки
Умение ясно и точно излагать свои мысли в письменной речи,
ответственное отношение к учению
Умножение многочленов.
Умножать многочлен на многочлен
Разложение многочлена на множители.
Разложение многочлена на множители (способ группировки)
Понимать смысл поставленной задачи, находчивость, активность
при решении задач
Умножать многочлен на многочлен, разложение многочлена на
множители способом группировки
61
Контрольная работа №6
6280
Проблемные задания,
фронтальный опрос,
упражнения
Индивидуальное решение контрольных
заданий. Контрольная
работа
Взаимопроверка в
парах; тренировочные
упражнения
Взаимопроверка в
парах; работа с текстом
Индивидуальное решение контрольных
заданий. Контрольная
работа
Глава V. Формулы сокращенного умножения
14
6263
§12.Квадра
т суммы и
квадрат
разности
5ч.
6466
6768
Возведение в квадрат и куб
суммы и разности двух выражений
Разложение на множители с
помощью формул квадрата
суммы и квадрата разности
§13.Разност
ь квадратов. Сумма
и разность
кубов
6ч.
Квадрат суммы и квадрат разности.
Применять формулы сокращенного умножения в преобразованиях
целых выражений в многочлены
Фронтальный опрос
Разложение многочлена на множители
Разложение многочленов на множители с помощью формул сокращенного умножения
Понимать смысл поставленной задачи, находчивость, активность
при решении задач
Применение формула разности квадратов
Взаимопроверка в
парах; решение проблемных задач
Разложение многочлена на множители
Разложение многочленов на множители с помощью формул сокращенного умножения
Разложение многочлена на множители
Разложение многочленов на множители с помощью формул сокращенного умножения
Построение алгоритма действия, решение
упражнений
Работа с опорными
конспектами, раздаточным материалом
Индивидуальное решение контрольных
заданий. Контрольная
работа
Фронтальный опрос;
работа с демонстрационным материалом
Формула разности
квадратов.
Умножение разности двух
выражений на их сумму
6970
Разложение разности квадратов на множители
7172
Разложение на множители
суммы и разности кубов
73
Контрольная работа №7
7476
7779
§14.Преобра
зование целых выражений
6ч.
Преобразование целого выражения в многочлен
Применение различных
способов для разложения на
множители
80
Контрольная работа №8
Преобразования выражения.
Разложение многочлена на множители
Применение формул сокращённого умножения, ля разложения
многочленов на множители
Умение ясно и точно излагать свои мысли в письменной речи,
ответственное отношение к учению
Преобразование выражения в многочлен
Разложение многочлена на множители различными способами
Преобразование выражений различными способами (формулы
сокращенного умножения и др)
Умение ясно и точно излагать свои мысли в письменной речи,
ответственное отношение к учению
Фронтальный опрос;
работа с демонстрационным материалом
Построение алгоритма действия, решение
упражнений
Индивидуальное решение контрольных
заданий. Контрольная
работа
15
8196
81
Глава VI. Системы линейных уравнений
§15.Линейн
ые уравнения с двумя
переменными и их
системы
5ч
Линейные уравнения с двумя переменными
8283
График линейного уравнения с двумя переменными
8485
Системы линейных уравнений с двумя переменными
8688
8991
9295
§16.Решени
е систем
линейных
уравнений
Способ подстановки
Способ сложения
Решение задач с помощью
систем уравнений
Уравнение с двумя переменными: решение
уравнений с двумя переменными
Проблемные задачи,
индивидуальный
опрос
Строить график линейного уравнения с двумя переменными
Системы двух линейных уравнений с двумя
переменными
Системы двух линейных уравнений с двумя
переменными: решение
подстановкой.
Решать графическим способом системы линейных уравнений с
двумя переменными
Взаимопроверка в
парах; работа с опорным конспектом
Практикум решение
качественных задач
Применять способ подстановки при решении систем линейных
уравнений с двумя переменными
Практикум решение
качественных задач
Системы двух линейных уравнений с двумя
переменными: решение
алгебраическим сложением
Решение текстовых
задач алгебраическим
способом.
Применять способ сложения при решении систем линейных уравнений с двумя переменными
Взаимопроверка в
группах; тренинг
Решать текстовые задачи, используя в качестве алгебраической
модели систему уравнений
Работа с опорными
конспектами, раздаточным материалом
Решение систем линейных уравнений, решение задач с помощью
систем
Умение ясно и точно излагать свои мысли в письменной речи,
ответственное отношение к учению
Индивидуальное решение контрольных
заданий. Контрольная
работа
96
Контрольная работа №9
97102
97
Определять, является ли пара чисел решением данного уравнения
с двумя переменными. Находить путём перебора целые решения
линейного уравнения с двумя переменными
Критичность мышления, умение распознать логически некорректные высказывания
Обобщающее повторение курса алгебры за 7 класс
Степень с натуральным
показателем и ее свойства
Решение качественных задач; работа с
раздаточным материалом
16
98
Разложение многочлена на
множители
99
Линейная функция.
.Функция
у = х2
100
зачет
101
Итоговая контрольная работа
102
Работа над
ошибками
Работа над ошибками
Применение формул сокращенного умножения, решение линейных уравнений, систем линейных уравнений
Решение линейных уравнений, систем линейных уравнений, преобразование многочленов, формулы сокращенного умножения
Умение контролировать процесс и результат учебной математической деятельности
Анализ собственных ошибок
Решение качественных задач; работа с
раздаточным материалом
Решение качественных задач; работа с
раздаточным материалом
Индивидуальное решение заданий.
Индивидуальное решение контрольных
заданий. Контрольная
работа
17
Лист корректировки
Причина корректировки
Название раздела, темы
(болезнь учителя, праздничДата
проведения ный день, отмена занятий по
по плану
приказу, курсовая подготовка,
сессия, семинар)
Корректирующие мероприятия (объединение тем,
домашнее изучение +
Дата
проведения
по факту
контрольная работа)
18
19