I. ПОЯСНИТЕЛЬНАЯ ЗАПИСКА.

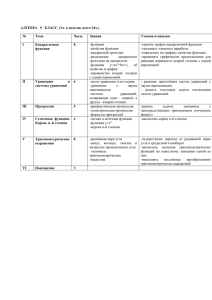
I. ПОЯСНИТЕЛЬНАЯ ЗАПИСКА.
Рабочая программа составлена с учетом положений Концепции долгосрочного социально-экономического
развития Российской Федерации на период до 2020 года. В настоящее время актуальной является проблема
совершенствования учебных программ, формирование допрофессиональных компетенций и усиление практической
направленности обучения, опираясь при этом на принцип сочетания профессиональных, морально-нравственных и
духовных качеств учащихся.
Реализация рабочей программы по элективному обеспечивает подготовку учеников к успешной сдаче ЕГЭ.
В настоящей программе учтены основные положения Концепции духовно-нравственного развития и воспитания
личности гражданина России. У учащихся формируются гражданские идеалы, патриотические чувства и активная
жизненная позиция.
Общие цели образования с учетом спецификации учебного предмета.
Данная программа по математике в 10 классе по теме "Практикум по математике» представляет углубленное
изучение теоретического материала укрупненными блоками. Курс рассчитан на обучающихся общеобразовательного
класса, желающих основательно подготовиться к сдаче ЕГЭ. В результате изучения этого курса будут использованы
приемы парной, групповой деятельности для осуществления элементов самооценки, взаимооценки, умение работать с
математической литературой и выделять главное.
Цели курса:

на основе коррекции базовых математических знаний суворовцев совершенствовать математическую культуру и
творческие способности обучающихся;

подготовить к вступительному экзамену;

овладеть определённым объёмом знаний, готовых методов решения нестандартных задач;

научить самостоятельно мыслить, творчески подходить к любой проблеме.
Изучение этого курса позволяет решить следующие задачи:

формирование у учащихся целостного представления о теме, ее значения в разделе математики, связи с другими
темами.

формирование поисково-исследовательского метода.

формирование аналитического мышления, развитие памяти, кругозора, умение преодолевать трудности при
решении более сложных задач.

осуществление работы с дополнительной литературой.

акцентировать внимание учеников на единых требованиях к правилам оформления различных видов заданий,
включаемых в итоговую аттестацию за курс полной общеобразовательной средней школы;

расширить математические представления учащихся по определённым темам, включённым в программы
вступительных экзаменов в другие типы учебных заведений.

реализация индивидуализации обучения; удовлетворение образовательных потребностей учащихся по алгебре.
Формирование устойчивого интереса учащихся к предмету.

выявление и развитие их математических способностей.

подготовка к обучению в ВУЗе.

обеспечение усвоения учащихся наиболее общих приемов и способов решения задач. Развитие умений
самостоятельно анализировать и решать задачи по образцу и в незнакомой ситуации;

развитие коммуникативных и общеучебных навыков, навыков самостоятельной работы, умений вести
дискуссию, аргументировать ответы.
Место и роль учебного предмета в достижении учащимися планируемых результатов освоения основной
образовательной программы училища.
Базисный учебный (образовательный) план на изучение элективного курса «Практикум по математике» в 10
классе отводит 34 часов в год. В соответствии с учебным планом образовательной организации для изучения
элективного курса отводится 1 ч в неделю.
Учебно-тематический план
Название темы
Текстовые задачи
Всего часов
8
Тригонометрия
Планиметрия
6
6
Стереометрия
Производная (6 часов)
8
6
II. Содержание элективного курса «Практикум по математике».
Текстовые задачи (8 часов)
Простейшие текстовые задачи. Текстовые задачи на движение. Текстовые задачи на работу. Текстовые задачи на
проценты, сплавы и смеси.
Тригонометрия (6 часов)
Преобразования числовых и буквенных тригонометрических выражений. Методы решения тригонометрических
уравнений.
Планиметрия (6 часов)
Вычисление длин и площадей. Задачи, связанные с углами. Углы и расстояния в пространстве
Стереометрия (8 часов)
Параллелепипед, куб. Призма. Пирамида. Составные многогранники
Производная (6 часов)
Применение производной к исследованию функций. Исследование тригонометрических функций.
III. РЕЗУЛЬТАТЫ ОСВОЕНИЯ РАБОЧЕЙ ПРОГРАММЫ
Требования к уровню подготовки обучающихся
Выполнение практических занятий имеет целью закрепить у учеников теоретические знания и развить
практические навыки и умения в области алгебры и геометрии, и успешной сдачи ЕГЭ по математике.
Учащиеся должны:

знать, что такое проценты и сложные проценты, основное свойство пропорции;

знать схему решения линейных, квадратных, дробно-рациональных, иррациональных уравнений;

знать способы решения систем уравнений;

знать определение параметра; примеры уравнений с параметром; основные типы задач с параметрами; основные
способы решения задач с параметрами. Знать определение линейного уравнения и неравенства с параметрами.
Алгоритмы решения линейных уравнений и неравенств с параметрами графическим способом. Определение
квадратного уравнения и неравенства с параметрами. Алгоритмы решения квадратного уравнения и неравенства с
параметрами графическим способом;

проводить тождественные преобразования иррациональных, показательных, тригонометрических выражений;

решать иррациональные, тригонометрические уравнения и неравенства.

решать системы уравнений изученными методами;

строить графики элементарных функций и проводить преобразования графиков, используя изученные методы;

применять аппарат математического анализа к решению задач;

применять основные методы геометрии (проектирования, преобразований, векторный, координатный) к
решению геометрических задач;

уметь применять вышеуказанные знания на практике.
Планируемые результаты изучения элективного курса «Практикум по математике» в 10 классе.
В ходе преподавания математики в 10-11 классах, работы над формированием у учащихся перечисленных в
программе знаний и умений следует обращать внимание на то, чтобы они овладевали умениями общеучебного
характера, разнообразными способами деятельности, приобретали опыт:

планирования и осуществления алгоритмической деятельности, выполнения заданных и конструирования новых
алгоритмов;

решения разнообразных классов задач из различных разделов курса, в том числе задач, требующих поиска пути
и способов решения;

исследовательской деятельности, развития идей, проведения экспериментов, обобщения, постановки и
формулирования новых задач;

ясного, точного, грамотного изложения своих мыслей в устной и письменной речи, использования различных
языков математики (словесного, символического, графического), свободного перехода с одного языка на другой для
иллюстрации, интерпретации, аргументации и доказательства;

проведения доказательных рассуждений, аргументации, выдвижения гипотез и их обоснования;

поиска, систематизации, анализа и классификации информации, использования разнообразных
информационных источников, включая учебную и справочную литературу, современные информационные
технологии.
Метапредметные результаты обучения алгебре в основной школе:
Математика, неоспоримо, является фундаментальной наукой и имеет широкое применение в самых различных
областях науки и техники. Среди учебных предметов она является базой для предметов естественного цикла. Такие
темы, как действия с обыкновенными и десятичными дробями, степени, формулы, функции, масштаб, уравнения,
широко применяются при решении практических задач физики, химии, биологии, географии, астрономии,
информатики, экономики.
Предметы естественно-математического цикла дают обучающимся знания о живой и неживой природе, о
материальном единстве мира, о природных ресурсах и их использовании в хозяйственной деятельности человека.
Общие учебно-воспитательные задачи этих предметов направлены на всестороннее гармоничное развитие
личности. Важнейшим условием решения этих общих задач является осуществление и развитие межпредметных
связей
предметов,
согласованной
работы
педагогов-предметников.
Изучение всех предметов естественнонаучного цикла тесно связано с математикой. Она дает учащимся систему
знаний и умений, необходимых в повседневной жизни и трудовой деятельности человека, а также важных для
изучения смежных предметов. На основе знаний по математике в первую очередь формируются общепредметные
расчетно-измерительные умения. Преемственные связи с курсами естественнонаучного цикла раскрывают
практическое применение математических умений и навыков. Это способствует формированию у учеников:

целостного, научного мировоззрения;
умение самостоятельно определять цели и задачи обучения, развивать мотивы и интересы познавательной
деятельности;

умение соотносить свои действия с планируемыми результатами, осуществлять контроль своей деятельности;

владение основами самоконтроля, самооценки, принятия осознанного выбора в математической учебной
деятельности;

умение создавать, применять знаки и символы;

смысловое чтение;

владение устной и письменной речью;

формирование и развитие компетентности в области использования информационно-коммуникационных
технологий.

Общими предметными результатами обучения математики в основной школе являются:

формирование представлений о математике как о методе познания действительности, позволяющем описывать и
изучать реальные процессы и явления;

развитие умений работать с учебным математическим текстом, точно и грамотно выражать свои мысли с
применением математической терминологии и символики, проводить логические обоснования, доказательства
математических утверждений;

развитие представлений о числе и числовых системах от натуральных до действительных чисел; овладение
навыками устных, письменных и инструментальных вычислений;

овладение символьным языком алгебры, приемами выполнения тождественных преобразований выражений,
решения уравнений и систем уравнений, неравенств; умение моделировать реальные ситуации языком алгебры;

овладение системой функциональных понятий, развитие умения использовать функционально - графические
представления для решения математических задач, описания и анализа реальных зависимостей.
Система (критерии) оценки знаний, навыков и умений.
С целью контроля и коррекции знаний обучающихся в соответствии с общими требованиями обучения и
развития к уровню подготовки выпускника предполагаются данной программой разные преимущественные формы
проверки достижений: устный опрос, развёрнутые письменные ответы на поставленные вопросы, самостоятельные
работы, тестирования, различные формы зачёта, контрольные работы.
Оценка устных ответов учащихся.
Ответ оценивается отметкой «5», если ученик:

полно раскрыл содержание материала в объеме, предусмотренном программой и учебником;

изложил материал грамотным языком в определенной логической последовательности, точно используя
математическую терминологию и символику;

правильно выполнил рисунки, чертежи, графики, сопутствующие ответу;

показал умение иллюстрировать теоретические положения конкретными примерами, применять их в новой
ситуации при выполнении практического задания;

продемонстрировал усвоение ранее изученных сопутствующих вопросов, сформированность и устойчивость
используемых при отработке умений и навыков;

отвечал самостоятельно без наводящих вопросов преподавателя. Возможны одна - две неточности при
освещении второстепенных вопросов или в выкладках, которые ученик легко исправил по замечанию преподавателя.
Ответ оценивается отметкой «4», если он удовлетворяет в основном требованиям на оценку «5», но при этом
имеет один из недостатков:

в изложении допущены небольшие пробелы, не исказившие математическое содержание ответа;

допущены один – два недочета при освещении основного содержания ответа, исправленные по замечанию
преподавателя;

допущены ошибка или более двух недочетов при освещении второстепенных вопросов или в выкладках, легко
исправленные по замечанию преподавателя.
Отметка «3» ставится в следующих случаях:

неполно или непоследовательно раскрыто содержание материала, но показано общее понимание вопроса и
продемонстрированы умения, достаточные для дальнейшего усвоения программного материала;

имелись затруднения или допущены ошибки в определении понятий, использовании математической
терминологии, чертежах, вы кладках, исправленные после нескольких наводящих вопросов преподавателя;

учащийся не справился с применением теории в новой ситуации при выполнении практического задания, но
выполнил задания обязательного уровня сложности по данной теме;

при знании теоретического материала выявлена недостаточная сформированность основных умений и навыков.
Отметка «2» ставится в следующих случаях:

не раскрыто основное содержание учебного материала;

обнаружено незнание или непонимание учеником большей или наиболее важной части учебного материала;

допущены ошибки в определении понятий, при использовании математической терминологии, в рисунках,
чертежах или графиках, в выкладках, которые не исправлены после нескольких наводящих вопросов преподавателя.
Оценка письменных контрольных работ учащихся
Отметка «5» ставится, если:

работа выполнена полностью;

в логических рассуждениях и обосновании решения нет пробелов и ошибок;

в решении нет математических ошибок (возможна одна неточность, описка, не являющаяся следствием
незнания или непонимания учебного материала).
Отметка «4» ставится, если:

работа выполнена полностью, но обоснования шагов решения недостаточны (если умение обосновывать
рассуждения не являлось специальным объектом проверки);

допущена одна ошибка или два-три недочета в выкладках, рисунках, чертежах или графиках (если эти виды
работы не являлись специальным объектом проверки).
Отметка «3» ставится, если:

допущены более одной ошибки или более двух-трех недочетов в выкладках, чертежах или графиках, но ученик
владеет обязательными умениями по проверяемой теме.
Отметка «2» ставится, если:

допущены существенные ошибки, показавшие, что учащийся не владеет обязательными умениями по данной
теме в полной мере
При организации процесса обучения в рамках данной программы предполагается применением следующих
педагогических технологий обучения: интерактивные, интегрированные, проектирование, творческие. Внеурочная
деятельность по предмету предусматривается в формах: конференций, викторин, олимпиад, презентаций.
Промежуточная аттестация проводится в соответствии с Положением о промежуточной аттестации учащихся
образовательной организации в форме тестирования.
IV.
УЧЕБНО-МЕТОДИЧЕСКОЕ
ОБРАЗОВАТЕЛЬНОЙ ДЕЯТЕЛЬНОСТИ
И
МАТЕРИАЛЬНО-ТЕХНИЧЕСКОЕ
ОБЕСПЕЧЕНИЕ
1.
Факультативный курс по математике. Решение задач. Шарыгин И.Ф.– М. – «Просвещение» 2008.
2.
Решение уравнений и неравенств. Гольдич В.А. Алгебра. - СПб.: Литера, 2008
3.
Изучение сложных тем курса алгебры в средней школе: Учебно – методические материалы по математике.
– М.: Илекса, Ставрополь: Сервисшкола, 2006.
4.
Решение сложных задач Единого государственного экзамена. Колесникова С. И. Математика. – М.: Айриспресс, 2005.
5.
Тематические тесты. Математика. ЕГЭ-2011. 10-11 классы/ Под редакцией Ф. Ф. Лысенко. – Ростов-наДону: Легион, 2009.
6.
Тестовые контрольные задания по алгебре и началам анализа./ Под редакцией Е. А. Семенко. –
Краснодар: «Просвещение – Юг», 2005.
7.
ЕГЭ. 2015. Математика. Типовые задания / под ред. А. Л. Семенова, И. В. Ященко. – М.: Издательство
«Экзамен», 2015.
8.
ЕГЭ. 3000 задач с ответами по математике / под ред. А. Л. Семенова, И. В. Ященко. – М.: Издательство
«Экзамен», 2011.- 511с.
9.
Математика ЕГЭ практикум С. Подготовка к выполнению части С И.Н.Сергеев, В.С.Панферов –
«Экзамен», М.2014
10.
ЕГЭ за 30 дней. Математика. Экспресс-репетитор/ АСТ. Астрель. Москва
11.
Тестовые задания по алгебре и началам анализа. Базовый уровень. / Под редакцией Семенко Е. А.,
Фоменко М. В., Белай Е. Н., Ларкин Г. Н. – Краснодар: Просвещение – Юг, 2008.
Календарно тематическое планирование элективного курса «Практикум по математике»
на 2015-2016 учебный год 10 класс.
№
урока
Дата
(неделя)
Название
Колраздела,
во
темы урока часов
1.09-12.09
Простейшие
текстовые
задачи
1-2
2
14.09-26.09
Текстовые
задачи на
движение
3-4
5-6
7-8
28.09-10.10
Текстовые
задачи на
работу
12.10-24.10 Текстовые
задачи на
проценты,
сплавы и
2
2
2
Элементы
содержания
Требования
к уровню подготовки
Виды контроля
Текстовые задачи (8 часов)
Простейшие
текстовые
задачи.
Проценты,
округление
с
самостоятельная
избытком,
работа(СР)
округление
с
недостатком. Выбор Знать: алгоритм решения
варианта из двух простейших
текстовых
возможных
задач; понятие процента,
Основные свойства, прямой
и
обратной
прямо и обратно
пропорциональности;
пропорциональные зависимости
СР
между
величины. Текстовые величинами.
задачи на движение. Уметь: составлять и решать
находить
Основные свойства, уравнения;
прямо и обратно процент от числа и число по
пропорциональные проценту; решать дробновеличины.
Выбор рациональные уравнения;
СР
округлять числа с избытком
оптимального
варианта. Текстовые и с недостатком.
задачи
на
совместную работу.
Проценты,
округление
с
СР
избытком,
округление
с
Тип и
форма
урока
Средства
нагляднос
ти
дидактичес
кие
материалы
УПЗУ,
УОСЗ
УПЗУ,
УОСЗ
дидактичес
кие
материалы
дидактичес
кие
материалы
УПЗУ,
УОСЗ
УПЗУ,
УОСЗ
дидактичес
кие
материалы
смеси
9-11
Преобразован
ия числовых и
буквенных
2.11-21.11
тригонометри
ческих
выражений.
Методы
решения
12-14 23.11-12.12 тригонометри
ческих
уравнений
3
3
недостатком.
Текстовые задачи на
проценты, сплавы и
смеси.
Тригонометрия (6 часов)
Вычисление
Знать:
основные
значений
тригонометрические
тригонометрических тождества;
формулы
выражений.
приведения; двойного угла,
Преобразования
суммы и разности синусов
числовых
и косинусов; формулы
тригонометрических понижения
степени;
выражений.
формулы перевода суммы в
Преобразования
произведение
и
буквенных
произведения в сумму;
тригонометрических алгоритм
решения
выражений.
простейших
тригонометрических
Тригонометрические уравнений.
использовать
уравнения
и Уметь:
изученные формулы для
неравенства.
преобразования
Простейшие
тригонометрические тригонометрических
и
решения
уравнения.
Два выражений
выполнять
метода
решения уравнений;
тригонометрических тождественные
уравнений: введение преобразования
новой переменной и тригонометрических
решать
разложение
на выражений;
тригонометрические
множители.
уравнения
методом
Однородные
тригонометрические введения новой переменной
и методом разложения на
уравнения.
множители;
решать
опорные
конспекты,
стенды,
таблицы
СР
УЗИМ,
УПЗУ
опорные
конспекты,
стенды,
таблицы
СР
УЗИМ,
УПЗУ
Вычисление
15-16 14.12-26.12 длин и
площадей
Задачи,
17-18 11.01-23.01 связанные с
углами
19-20
Углы и
25.01-6.02 расстояния в
пространстве
2
2
2
однородные
тригонометрические
уравнения.
Планиметрия (6 часов)
Треугольник.
Параллелограмм,
прямоугольник,
ромб,
квадрат.
Трапеция.
Знать: определения,
Окружность и круг.
признаки и основные
Многоугольник.
свойства плоскостных
Правильные
фигур (треугольника,
многоугольники.
квадрата, прямоугольника,
Окружность,
параллелограмма, ромба,
вписанная
в
трапеции); понятия
треугольник,
и
окружности, вписанных и
окружность,
описанных углов и
описанная
около
многоугольников; понятие
треугольника. Сумма
вектора на плоскости.
углов
выпуклого
Уметь: применять свойства
многоугольника.
и признаки при решении
Вписанная
планиметрических задач;
окружность
и
находить сумму и разность
описанная
векторов с помощью
окружность
правила треугольника,
правильного
выражать один из
многоугольника.
коллинеарных векторов
Величина угла,
через другой; строить
градусная мера угла,
чертеж задачи.
соответствие между
величиной угла и
длиной дуги
окружности.
Координатная
СР
УПЗУ,
УОСЗ
опорные
конспекты,
стенды,
таблицы
опорные
конспекты,
стенды,
таблицы
СР
УПЗУ,
УОСЗ
СР
УПЗУ,
УОСЗ
опорные
конспекты,
стенды,
таблицы
21-22
23-24
25-26
27-28
8.02-20.02
Параллелепип
ед, куб
24.02-5.03 Призма
9.03-19.03 Пирамида
Составные
многогранник
21.03-9.04
и
2
2
2
2
плоскость. Векторы.
Вычисление длин и
площадей.
Стереометрия (8 часов)
Параллелепипед;
Знать: основные понятия
куб; симметрии в стереометрии, основные аккубе,
в сиомы стереометрии;
параллелепипеде.
элементы тетраэдра и
Сечения
куба, параллелепипеда, свойства
параллелепипеда.
противоположных граней и
Призма, ее
его диагоналей;
основания, боковые определение
ребра, высота,
прямоугольного паралбоковая
лелепипеда, куба, свойства
поверхность; прямая прямоугольного
призма; правильная параллелепипеда, куба;
призма. Сечения
элементы многогранника:
призмы.
вершины, ребра, грани,
Пирамида,
ее формулу площади полной
основание, боковые поверхности прямой
ребра,
высота, призмы, определение
правильной призмы.
боковая
Уметь: распознавать на
поверхность;
чертежах и моделях
треугольная
пространственные формы,
пирамида;
описывать взаимное
правильная
пирамида. Сечения расположение точек,
прямых, плоскостей с
пирамиды.
помощью аксиом
стереометрии, применять
Площадь
аксиомы при решении
поверхности
задач; распознавать на
составного
чертежах и моделях
многогранника.
параллелепипед и тетраэдр
СР
УЗИМ,
УПЗУ
модели
тел,
развертки
модели
тел,
развертки
СР
УЗИМ,
УПЗУ
модели
тел,
развертки
СР
СР
УЗИМ,
УПЗУ
УЗИМ,
УПЗУ
модели
тел,
развертки
11.04-30.04
29-31
Применение
производной к
исследованию
функций.
32-34
Исследование
3.05-25.05 тригонометри
ческих
функций
3
3
и изображать на плоскости,
строить сечение
плоскостью, параллельной
граням параллелепипеда,
тетраэдра; строить
диагональные сечения в
параллелепипеде,
тетраэдре; сечения
плоскостью, проходящей
через ребро и вершину
параллелепипеда
Производная (6 часов)
Уравнение
Знать:
понятие
касательной
к производной;
графику
функции. формулу
производной
Вторая производная степенной функции;
и ее геометрический формулы
производных
и
физический тригонометрических
смысл. Исследование функций;
функций.
правила
Применение
дифференцирования;
производной
к уравнение касательной;
исследованию
понятие точек экстремума
функций
функции;
понятие
и построению
наибольшего
и
графиков.
наименьшего
значений
Наибольшее
и функции;
наименьшее
схему
исследования
значение функций
функции на монотонность и
экстремумы.
Уметь:
находить
Применение
производную
степенной
производной к
функции,
пользуясь
исследованию
таблицей производных;
функций
дидактичес
кие
материалы
СР
УЗИМ,
УПЗУ,
УОСЗ
СР
УЗИМ,
УПЗУ,
УОСЗ
дидактичес
кие
материалы
и построению
графиков.
Исследование
тригонометрических
функций.
находить
производные
тригонометрических
функций;
находить
производные
функций,
пользуясь
правилами
дифференцирования;
применять
производную
для исследования функций;
находить
производную
сложной функции;
применять
производную
для отыскания наибольшего
и наименьшего значений
функции
*Условные обозначения:
1. СР – самостоятельная работа;
2. УПЗУ – урок применения знаний и умений;
3. УОСЗ – урок обобщения и систематизации знаний;
4. УЗИМ – урок закрепления изученного материала.