Рис. 8.2

8.2. ПРИМЕНЯЕМЫЕ РАЗНОВИДНОСТИ ТЕОРИИ ПОЛЗУЧЕСТИ БЕТОНА.
РЕЛАКСАЦИЯ НАПРЯЖЕНИЙ
C (t, 2)
В пределах линейных зависимостей (8.6), (8.7) теории ползучести
отличаются друг от друга описанием меры ползучести. Согласно теории
старения меру ползучести можно определить по формуле
C t ,    C t   C   ,
(8.10)
где C t  – мера ползучести в момент времени t; C   – то же, в момент
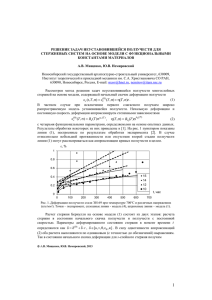
времени . Кривая, например, Ct , 2   Ct ,1   C 2  , т.е. получается из
кривой более раннего возраста путем отсечения и параллельного переноса той
её части, которая соответствует разности возрастов загружения (рис. 8.2, (а)).
C (t,  1)
C, см2/кН
C (1)
C (2)
C (t, 1)
C, см2/кН
O
0 1
t
2
t
O
t
1
2
3
t
(б)
(а)
Рис. 8.2
Эта теория получила
широкое распространение из-за своей
относительной простоты. Задача о релаксации (падении) напряжений в стержне
(рис. 8.1, (б)) решается в этой теории достаточно просто.
Предположим, что в момент времени t0 введена вынужденная
деформация  t0    0  const . В этом случае уравнение релаксации (8.4)
принимает вид
 t

Rt , 

.
 t   E t  0 1  Rt , d , Rt ,  
E t 


 t0

Но Et  0   t  – есть упругомгновенное напряжение. Тогда
 t


 t    t  1  Rt ,  d    t H t ,   ,


 t0




(8.11)
(8.12)
ОСНОВНЫЕ ЗАВИСИМОСТИ И НЕКОТОРЫЕ ЗАДАЧИ ТЕОРИИ ПОЛЗУЧЕСТИ
207
где   t  – напряжение в стержне с учетом ползучести;  t  –
упругомгновенное напряжение; H t ,   – коэффициент затухания напряжений.
Определим напряжение   t  путем непосредственного решения
уравнения релаксации (8.13), без построения ядра Rt ,  
t

 t   E t     K t ,  d   0 E t  .

(8.13)
t0
Обозначим ядро интегрального уравнения (8.13)
Lt ,    E t K t ,    E t 
В теории старения
 t ,  
.

(8.14)
 1

 1
 
 E    C t   C    E t   E    C  




Здесь и далее точкой обозначена производная по .
В случае, если E    E t   E  const
L t ,     E C   ,
L t ,   E t 


и уравнение (8.13) принимает вид
t

  t       E C   d   0 E .
(8.15)
t0
Продифференцировав уравнение (8.15) по t, получим
(8.16)
  t   E C   t   0 .
Здесь и далее точками обозначены производные по t. Общее решение этого
линейного однородного дифференциального уравнения
 t   C1e

t
E

С   d  C1e  E C t C t0  .
t0
Принимая во внимание, что EC t    t  – характеристика ползучести, и
определив произвольную постоянную С1 из начального условия
  t    t0  , окончательно получим
t t0
  t    t0 e  t  t0  .
(8.17)
Поскольку, при E  const  t    t0  то, сравнивая выражения (8.12) и
(8.17), получим
t

1  Rt ,  d  H t , t 0   e  t  t0  .
t0
(8.18)
ОСНОВНЫЕ ЗАВИСИМОСТИ И НЕКОТОРЫЕ ЗАДАЧИ ТЕОРИИ ПОЛЗУЧЕСТИ
208
Особенностью этого решения является то, что оно получено без
предварительной аппроксимации характеристики ползучести  t  . Резольвента
Rt ,  ядра L t ,      в данном случае определяется выражением
d   
Rt ,    e  t 
e .
(8.19)
d
Это легко проверить подстановкой выражения (8.19) в левую часть равенства
(8.18)
Для нестареющих материалов, у которых свойства инвариантны
относительно начала отсчета времени, модуль упругости постоянен, а ядра
ползучести и релаксации зависят только от разности аргументов t и . Кривые
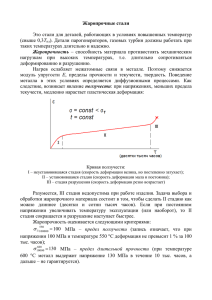
меры ползучести в теории упругой наследственности не зависят от возраста
загружения
 ; одна кривая получается из другой путем сдвига последней вдоль оси t (рис.
8.2, (б)). Для описания меры ползучести принимают обычно следующее
выражение
C t     C0 f t   , f t     1  e  1 t   .
(8.20)
Значения С0 и  1 зависят от свойств материала. При t     Ct     C0 ;
следовательно С0 – предельная мера ползучести f t    – функция,
учитывающая длительность действия нагрузки.
С учетом (8.20) уравнение релаксации (8.13) принимает вид
t

 t    1    e  1 t  d   t0  ,

(8.21)
t0
где   EC0 – предельная характеристика ползучести;  t0   E 0 .
Продифференцировав по t уравнение (8.21) получим такое уравнение
t

 * t    1  t    12    e  1 t   d  0 .
(8.22)
t0
Умножив уравнение (8.21) на  1 и сложив его с (8.22) получим следующее
дифференциальное уравнение
(8.23)
 * t   r  t    t 0 , r   1 1    .
Решение этого уравнение следующее
1   e  r  t t 0 
 t    t0 H t , t0    t0 
.
1

(8.24)
При t   коэффициент затухания напряжений
H t , t0  
В этом случае
1
.
1
(8.25)
ОСНОВНЫЕ ЗАВИСИМОСТИ И НЕКОТОРЫЕ ЗАДАЧИ ТЕОРИИ ПОЛЗУЧЕСТИ
    
209
E
 0  EД  0 ,
1 
(8.26)
т.е. при постоянных напряжениях деформация переходит в упругую с
длительным
модулем
упругости
Ед.
Резольвента
ядра
Rt , 
  1  t  
Lt ,    1e
определяется выражением
Rt      1e  r t   .
(8.27)
Теория старения постулирует полную необратимость деформаций ползучести;
теория упругой наследственности, наоборот предполагает полную обратимость
этих деформаций. Как следствие, теория старения приводит к большему
затуханию напряжений.
Наследственная теория старения (теория упругоползучего тела) – это
синтез двух предыдущих теорий. Кривые мер ползучести в этой теории
представлены через произведение двух функций
(8.28)
Ct ,   С , t     C0  f t    ,
где  t  – монотонно убывающая функция возраста (учитывает старение
материала). Для описания свойств старения бетона обычно принимают
   c  de  , c  0,5 ,
(8.29)
для описания функции f t    – выражение (8.20). Соответствующие этим
функциям кривые показаны на рис. 8.3.


C0 ()
f (t)
C0
O
(а)

O
(б)
t–
Рис. 8.3
При необходимости учета быстронатекающей ползучести для описания
f t    принимают такие формулы
f t     1  Be  1 t   , B  0,8 ,
(8.30)
f t     1  Be  1 t    B2 e  2 t   , B1  B2  1 .
(8.31)
В случае описания меры ползучести формулами (8.28), (8.29), (8.30) при В = 1
ядро ползучести принимает вид
ОСНОВНЫЕ ЗАВИСИМОСТИ И НЕКОТОРЫЕ ЗАДАЧИ ТЕОРИИ ПОЛЗУЧЕСТИ
 E ( )
 1 t   






L t ,   E t  

C

(

)
f
t



C


e
.
0
0
2


E



210
(8.32)
Уравнение релаксации теперь приводится к дифференциальному уравнению
второго порядка с переменными коэффициентами. Решение этого уравнения
дает следующую формулу для коэффициента затухания напряжений
H t ,    1   1
где
  t0 
E t0 
t

E   e   d ,   E t0  C0 ,
(8.33)
t0


     1 1   t ,  d,  t ,   E   C0    .
(8.34)
t0
Ядро релаксации
t


1 


  

R t ,  
   e
E   e d  (8.35)
E     1 E       1
E t  


t0


при E    E  const коэффициент затухания напряжений (8.33) можно


вычислить по следующим формулам
H t , t0   1 
где
ab
F t0   F1 t  t0 Lt  t0  ,
1 b

1  e  1 t  t0  
Lt  t0   exp   1 1  b t  t0   a
,



F1 t  t0   1 


 1m a me  mt  t  ,
1
F t0   1 

m 1
t0
 1m a m ,
Fm
(8.37)
0
Fm
m 1

(8.36)
(8.38)
m
Fm 
 (1  b  i ) ,
(8.39)
i 1
a  de , b  c,   EC0 ,     1 .
(8.40)
Определим предельное значение коэффициента затухания напряжений
H ,t0  в стержне, выполненном из эталонного бетона считая, что
вынужденная деформация  0  const введена в возрасте бетона t0  28 сут.
Эталонным считается бетон со следующими характеристиками: Е = 3,3 
.104 МПа; С0.=.6,36.·.10–5 МПа;   2,1;  1  0,006 сут1 ;   0,012 сут1 ;
  2; d  0,7; a  1,05; b  1,05.
Воспользуемся формулами (8.36) – (8.39). При t  
Lt , t0   F1 t  t0   0,
ОСНОВНЫЕ ЗАВИСИМОСТИ И НЕКОТОРЫЕ ЗАДАЧИ ТЕОРИИ ПОЛЗУЧЕСТИ
211

ab
a b
a
a2


H , t0   1 
F t0   1 
1



1 b
1  b  1  b   1  b    1  b  2  

1,05  1,05 
1,05
1,052
1 
  0,200.
 1

1  1,05  1  1,05  2 1  1,05  2 1  1,05  4 
При определении H ,t0  оказывается достаточным удержание двух членов
ряда (8.39). В случае применения теории старения (8.18) H ,t0  = е- = е-2,1 =
= 0,122 согласно теории упругой наследственности (8.25) H ,t0  = 1/ (1+2,1) =
= 0,323. Результат, полученный по наследственноственной теории старения,
занимает промежуточное положение. Этот пример показывает, что за счет
ползучести, в случае постоянных вынужденных деформаций, напряжения
могут существенно снижаться (релаксировать). Отметим также сравнительную
сложность решения (8.36), которое к тому же построено для частного вида
описания меры ползучести и постоянного модуля упругости. Если деформации
являются вынужденными и изменяются во времени по закону  t  , то
определение напряжений, является задачей обобщенной релаксации.
Напряжение находят по формуле (8.4), что при наличии резольвенты Rt ,   , не
вызывает затруднений. Задача обобщенной релаксации чаще всего встречается
при определении температурных напряжений, когда распределение
температуры T t  вызывает температурные деформации  t   T t .
Численные методы решения задач теории ползучести основаны на
возможности представления физических соотношений в алгебраической форме.
Если рассматриваемый отрезок времени t  t0 разбить на n промежутков и
зафиксировать моменты времени t0 , t1 ,  , tk ,  tn то
(8.41)
{ }  K  { } ,
 t0 
  00
  t 

 1 
 10
 : 
 
{ }  
, K   
 t k 
 k 0
 : 
 






t
 n 
 n0




11
 k1



 kk

 n1

 nk

Причем коэффициенты матрицы ползучести
образом
 kk   tk , k  
1
E  k 
K 

 t0 

 t 

 1 

  
,
{

}


 .(8.42)




t
 k 

  






 nn 

t
 n 
определяется следующим
 C tk , k ,
 ki   tk , i    tk , i 1  
1

1
E  i  E  i 1 
 C tk , i   C tk , i 1  ,
(8.43)
ОСНОВНЫЕ ЗАВИСИМОСТИ И НЕКОТОРЫЕ ЗАДАЧИ ТЕОРИИ ПОЛЗУЧЕСТИ
212
ti  ti 1
, i  0, 1, 2,  , n  1, k  1, 2,  , n .
2
Связь между напряжениями {} и деформациями {} устанавливается
i 
зависимостью
{ }  R{ }  E0 R { }, E0  E t0  ,
(8.44)
где R   K  – резольвентная матрица; R   R E0 – приведенная матрица.
Так как матрица K  – нижняя треугольная, то и матрица R  – также нижняя
треугольная
1
 r00
r
 10
 
R  
rk 0
 

 rn 0
r11

rk1



rkk

rn1

rnk





.



rnn 
(8.45)
Ее элементы могут быть вычислены по следующим формулам
1
rkk 
, rki  rkk
 kk
k j
 r
kj jk
.
(8.46)
j 1
Для случая описания модуля упругомгновенных деформаций и меры
ползучести такими зависимостями
E   Ei 1  0,372e 0 ,026 τ , Ei = 3,54  104 МПа,





С т,   Ci 0,5  0,7e 0 ,012 τ 1  0,85e 0,006 t    0,15e 0,3t   ,
Ci  2,6 10 5 MПа
и моментов времени, определяемых вектором {t} сут.
{t}  40 60 130 180 260 360,
приведенная резольвентная матрица
(8.46) имеет вид
1

 0,074

  0,061
R    0,055
 0,049

 0,044
 0,040
R , построенная
0,907
 0,124
0,947
 0,108  0,128
0,978
 0,094  0,107  0,122
 0,082  0,087  0,087
 0,075  0,075  0,067
(8.47)
по формулам (8.43),





 . (8.48)

0,995

 0,123
0,985

 0,075  0,122 0,979
ОСНОВНЫЕ ЗАВИСИМОСТИ И НЕКОТОРЫЕ ЗАДАЧИ ТЕОРИИ ПОЛЗУЧЕСТИ
213
С помощью матрицы R  легко определяются коэффициенты затухания
напряжений, правда для фиксированных моментов времени, определяемых
вектором {t}. Так, для того, чтобы определить H t ,t0  – необходимо
умножить последнюю строку матрицы
H 360, 40  0,525 .
R 
на единичный вектор {}: