Методы решения одномерных стохастических краевых задач
реклама

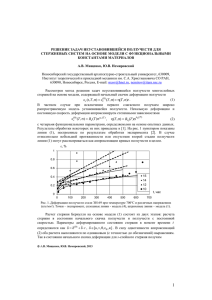
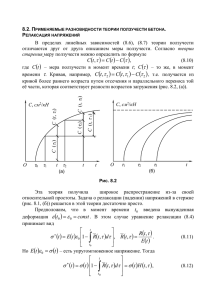
МЕТОДЫ РЕШЕНИЯ ОДНОМЕРНЫХ СТОХАСТИЧЕСКИХ КРАЕВЫХ ЗАДАЧ ПОЛЗУЧЕСТИ Н. Н. Попов Самарский государственный технический университет, Самара, Россия В настоящее время в условиях повышения требований к надежности и прочности элементов конструкций весьма актуальной проблемой механики деформируемого твердого тела стал учет стохастических неоднородностей материала, которые обусловлены различными технологическими и структурными факторами. Эта проблема является особенно важной для элементов конструкций, работающих в условиях ползучести, поскольку известно, что опытные данные по деформации ползучести, полученные при испытаниях на стандартных образцах, имеют значительный разброс. В данной работе построено аналитическое решение стохастической нелинейной краевой задачи установившейся ползучести для толстостенной трубы, находящейся под действием внутреннего давления q. Задача рассматривается в цилиндрических координатах для случая плоского деформированного состояния, в предположении, что стохастические свойства материала трубы описываются при помощи случайной функции одной переменной (радиуса r). Определяющие соотношения ползучести принимаются в соответствии с нелинейной теорией вязкого течения в стохастической форме [1] n 1 n 1 3 (1) r c r 1 U r , 2 2 где σ φ и σ r – компоненты тензора напряжений, ε φ и ε r – компоненты тензора дефор- маций, c и n – постоянные материала. С помощью случайной однородной функции U ( ) U 0, U 2 1 описываются флуктуации реологических свойств материала, а число α ( 0 α 1) играет роль коэффициента вариации этих свойств, – символ математического ожидания; точка обозначает дифференцирование по времени. К определяющим соотношениям ползучести (1) присоединяются уравнение равновесия для напряжений d r r 0, dr r условие совместности деформаций, сформулированное для скоростей деформаций (2) d r 0 (3) dr и граничные условия r (a) q , r (b) 0 , где a и b соответственно внутренний и внешний радиусы трубы. Решение системы уравнений (1) – (3) сводится к статистически нелинейному уравнению второго порядка относительно радиального напряжения σ r (штрихом обозначается дифференцирование по r ) r r 1 U (r ) r n2 r 1 U (r ) r U (r ) r 0 . n n (4) 1 Используя метод разложения радиального напряжения в ряд по степеням малого параметра α в уравнении (4) r r 0 k rk , r r 0 , rk 0, k 1, 2,3,..., k 1 можно получить систему статистически линейных дифференциальных уравнений n2 n2 r r r0 r0 0 , r r1 r1 U r0 , n n n n2 r k 1 r rk rk U rk 1 U rk 2 U 2 rk 3 1 U k 1 r0 , k 2,3, 4, , n n из которой можно найти составляющие радиального напряжения с любой степенью точности. Найдены средние значения и дисперсии случайного поля напряжений и скоростей деформаций с учетом членов до четвертого приближения метода малого параметра. При этом предполагалось, что случайная функция U ( ) , задающая поле возмущений реологических свойств материала, распределена по нормальному закону с корреляционной функцией K ( ) e cos 1 sin , r2 r1 , γ 0 , где γ и β – постоянные величины, определяемые по опытным данным из условий наилучшей аппроксимации. Проведен статистический анализ случайного поля напряжений и скоростей деформаций в зависимости от показателя нелинейности и степени неоднородности материала. Получено, что для слабонеоднородных материалов ( α 0,1 ÷0,3) вклад, вносимый в решение четвертым приближением незначителен, и можно ограничиться третьим приближением. Для материалов с существенной неоднородностью ( α 0, 4 ÷0,5) неучет членов четвертого порядка малости может привести к необоснованному завышению показателей прочности и надежности цилиндрических элементов конструкций. Также рассматривается в условиях ползучести всестороннее растяжение усилиями p бесконечной пластины из стохастически неоднородного материала, ослабленной круговым отверстием радиуса a. Задача решается в полярной системе координат для случая плоского напряженного состояния, в предположении, что стохастические свойства материала пластины описываются при помощи случайной функции одной переменной (радиуса). Определяющие соотношения ползучести, взятые в соответствии с нелинейной теорией вязкого течения, принимаются в стохастической форме [2] r 0,5cs n1 2 r H r , 0,5cs n1 2 r H r , H (r ) 1 U r , (5) где s 2 r2 2 r – интенсивность напряжений. Граничное условия и условие на бесконечности имеют вид r ( a ) 0 , r ( ) p . (6) Случайная функция U (r ) , задающая флуктуации реологических свойств материала, была взята в виде U (r ) 0 J 0 (r ) 2 k J k (r ) , где k – независимые случайные велиk 1 чины с математическим ожиданием k 0 и дисперсией k2 1 , J k (r ) – функция Бесселя I рода целого порядка. Путем введения новых переменных s и по формулам r 2s cos / 3 , 2s cos / 3 / 3 , краевая задача (2), (3), (5), (6) сводится к системе стохастических нелинейных дифференциальных уравнений 2 d dH cos / 3 3 cos n sin H sin cos , dr dr r , (7) 2 2 s cos / 3 H ds dH (cos 2 n sin 2 ) H s sin 2 dr dr r с граничным условиям ( a ) и условием на бесконечности s() p . 2 Линеаризация системы уравнений (7) проводилась на основе первого приближения метода малого параметра. Линейная система решалась численно методом Адамса пятого порядка[3]. В результате статистического анализа случайного поля напряжений получено, что дисперсия тангенциального напряжения принимает наибольшее значение на конту(cos 2 n sin 2 ) H ре отверстия, а дисперсия радиального напряжения r на этом контуре равна нулю. При удалении от контура отверстия дисперсии напряжений достаточно быстро приближаются к постоянным значениям, совпадающим с их значениями для бесконечной пластины без отверстия. В таблице приведены значения коэффициента вариации D 0 100% , где D – дисперсия тангенциального напряжения , на границе от верстия r a в зависимости от степени нелинейности ползучести материала n и степени неоднородности материала . n 0,1 0,2 0,3 0,4 0,5 1 2 4 6 8 5,45 3,47 2,03 1,44 1,12 10,9 6,94 4,06 2,88 2,24 16,35 10,41 6,03 4,32 3,36 21,8 13,88 8,12 5,76 4,46 27,25 17,35 10,15 7,20 5,60 Максимальный разброс напряжений (по правилу трех сигма) характеризуется утроенным коэффициентом вариации. Так, например, при n 2 и 0.3 максимальный разброс тангенциального напряжения около среднего значения равен 31,23%. ЛИТЕРАТУРА 1. Должковой А.А., Попов Н.Н., Радченко В.П. Решение стохастической краевой задачи установившейся ползучести для толстостенной трубы методом малого параметра // ПМТФ. – 2006. – Т. 47. – № 1. – С. 161–171. 2. Попов Н.Н. Ползучесть стохастически неоднородной пластины с круговым отверстием // Вестник Самарск. госуд. техн. ун-та. Серия: Физ.-матем. науки. – 2008. – № 2 (17). – С. 126–132. 3. Бахвалов Н.С. Численные методы. Т.1. – М.: Наука, 1975. – 632 с. 3