математика, 9 класс
реклама

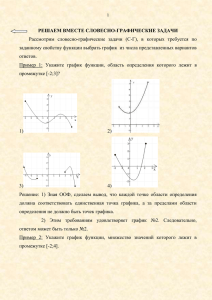
ХКЗФМШ – 2011/12 МАТЕМАТИКА, 9 КЛАСС Кармакова Тамара Сергеевна, Табачук Наталья Петровна, ДВГГУ Задачи на графиках в курсе математики основной школы Тема «Задачи на графиках» выбрана не случайно: в соответствии с контрольными измерительными материалами по итоговой аттестации за курс основной школы задания по теме «Функции и графики» направлены на проверку следующих умений: - строить графики изученных функций и отвечать на вопросы, связанные с их исследованием; - на основе графиков изученных функций строить более сложные графики (кусочно-заданные, с «выбитыми» точками и т.п.); - использовать графические представления и свойства функций для решения математических задач из других разделов курса (например, для исследования уравнений, неравенств и систем уравнений). В этой статье представлены пять классов задач: словесно-графические, графическо-словесные; аналитико-графические, графическо-аналитические, графическо-графические. В основу классификации взяты языки, описывающие условие задачи и полученный ответ, причем одним из них является язык графических изображений. Под словесно-графическими задачами (С-Г) будем понимать задачи, в которых даны свойства функции и требуется найти из заданных графиков тот, который обладает этими свойствами. Решить словесно-графическую задачу значит перейти от словесного способа задания функции к графическому. Эти задачи направлены на отработку умений по заданным свойствам функции находить ее график. Рассмотрим пример решения такой задачи. Задача 1. Даны свойства функции: а) Область определения функции есть промежуток [-3;5]; б) Значения функции составляют промежуток [-4;3]; в) Наибольшее значение функции равно 3; г) Отрицательные значения функция принимает в промежутке (-3;1). Хабаровск - 2011 Математика – 9: Задачи на графиках в курсе математики основной школы Укажите график функции, обладающей данными свойствами. 1) 2) 3) 4) Рассмотрим решение по шагам: Шаг 1: Укажем график функции, область определения которого лежит в промежутке [-3;5]. Зная ООФ, сделаем вывод, что каждой точке области определения должна соответствовать единственная точка графика, а за пределами области определения не должно быть точек графика. Этим требованиям удовлетворяют графики №2и №3. Шаг 2: Укажем график функции, множество значений которого лежит в промежутке [-4;3]. Зная множество значений функции, можно сделать вывод, что этому требованию удовлетворяют графики №2 и №4. Шаг 3: Укажем график функции, наибольшее значение которой равно 3. Данному условию удовлетворяет график №1, №2 и №4. Шаг 4: Функция задана на промежутке [-3;5]. Зная промежутки, на которых функция отрицательна, можно сделать вывод, что на данных промежутках график функции должен располагаться ниже оси Ох. Видим, что данному условию удовлетворяет график №2 и №3. Обобщая полученные результаты, можем сделать вывод, что всеми четырьмя свойствами обладает график функции, изображенный на рисунке №2. Под графическо-словесными задачами (Г-С) будем понимать задачи, в которых задан график функции, и требуется описать его свойства. Решить Г-С задачу значит перейти от графического способа задания функции к словесному. Кармакова Т.С., Табачук Н.П. ХКЗФМШ – 2011/12 Эти задачи направлены на отработку умений читать графики. Рассмотрим пример решения такой задачи. Задача 2. Функция y=f(x) задана графиком: Найдите по графику: 1) область определения функции; 2) множество значений функции; 3) определите четность, нечетность функции; 4) промежутки возрастания и убывания функции; 5) нули функции; 6) наибольшее и наименьшее значения функции; 7) промежутки знакопостоянства. Решение: 1.Воспользуемся алгоритмом нахождения ООФ: 1) Спроектируем график на ось Ох; 2)Сделаем вывод: х ___. 2.Воспользуемся алгоритмом нахождения МЗФ: 1)Спроектируем заданный график на ось ординат; 2)Сделаем вывод: у ___. 3.Воспользуемся алгоритмом определения четности: 1)Из графика функции видим, что график функции не обладает никакой симметрией; 2)Делаем вывод, что функция является ________________________. 4.Воспользуемся алгоритмом нахождения промежутков возрастания и убывания функции: 1)Разобьем заданный график на участки «подъема» и участки «спуска»; 2)Делаем вывод: на промежутках ___________________- возрастает; _______________________ - функция убывает. Хабаровск - 2011 Математика – 9: Задачи на графиках в курсе математики основной школы 5.Воспользуемся алгоритмом для определения нулей функции: 1)Анализируем расположение графика относительно оси Ох; 2)Делаем вывод: график пересекает ось Ох в точках х1=____, х2=____. 6. Воспользуемся алгоритмом для определения наибольшего и наименьшего значений функции: 1)Анализируя график, находим множество значений функции у [-5;3]. 2)Делаем вывод: унаиб= ___, унаим=___. 7. Воспользуемся алгоритмом для нахождения промежутков знакопостоянства: 1) Спроектируем на ось Ох те участки графика, которые расположены над осью абсцисс: х ____________________; 2) Спроектируем на ось Ох те участки графика, которые расположены под осью абсцисс: х ____________________; 3) Запишем ответ: y>0, если х ___________________ y<0, если х ___________________. Сравните полученные вами ответы с представленными в таблице. № задания ответ 1 2 3 [-6;5] [-5;3] Ни четная, ни нечетная 4 5 [-6;-4] и х1=1; [2;2] и [3;5]- х2=3 возрастает; [-4;-2] и [2;3]убывает 6 7 унаиб=3 унаим=-5 y>0, x (-6;1) y<0, x (1;5) Под аналитико-графическими задачами (А-Г) будем понимать задачи, в которых дана формула (или формулы) и требуется найти соответствующий график. Решить аналитико-графическую задачу значит перейти от аналитического задания функции к графическому. Аналитико-графические задачи направлены на отработку умений находить соответствующие графики основных элементарных функций по заданной формуле (или формулам); кусочно-заданных функций; функций, область определения которых содержит «выбитые» точки и функций, полученных в результате последовательной деформации формулы некоторой исходной элементарной функции. Рассмотрим примеры аналитико-графических задач и способы их решения. Кармакова Т.С., Табачук Н.П. ХКЗФМШ – 2011/12 Задача 3. Функция задана формулой у=х2–3х+4. По заданной формуле выбрать график из числа представленных вариантов ответа. 1) 2) 3) 4) Решение: 1. Исходя из заданной формулы, можно сделать вывод, что ветви параболы направлены вверх. Этому условию удовлетворяют графики под №1, №3, №4. 3 7 2 4 Вершина параболы находится в точке ( ; ), этому условию удовлетворяет только график №1. 2. Проверим правильность выбора, построив несколько точек: x1=0, f(0)=4; x2=3, f(3)=4; x3=1, f(1)=2; x4=2, f(2)=2. Следовательно, ответ №1. 1 , х 1; Задача 4. Укажите график функции, заданной формулами у= х х 2 , х 1. 1) 2) Хабаровск - 2011 Математика – 9: Задачи на графиках в курсе математики основной школы 3) 4) Решение: 1) Анализируя формулу можно сделать вывод, что ответом может быть график, состоящий из графиков двух функций, одна из которых гипербола на промежутке х 1, другая – парабола на промежутке х<1. Данным требованиям удовлетворяет график №4. 2) Проверим правильность выбора контрольными точками (1;1) и (0;0). 3) Записываем ответ: №4. Задача 5. Для каждой функции, заданной формулой, укажите ее график. 1) у=-х+1; 2) у=х-1; а) b) 3) у=х2-1 c) Решение: 1) Проанализировав содержание задачи, можно сделать вывод о том, что эта задача на соотнесение, т.е. для каждой формулы должен быть найден соответствующий график; 2) Анализируя формулы, можно сделать вывод, графиками формул №1 и №2 должны быть прямые, этому требованию удовлетворяют графики а) и b), следовательно, формуле №3 соответствует график с). Поскольку в формуле №1 коэффициент при х равен -1, то график функции должен убывать. Этому требованию удовлетворяет только график №2, следовательно, формуле №2 соответствует график а). 3) Запишем ответ: №1b, №2a, №3c. Под графическо-аналитическими задачами (Г-А) будем понимать задачи, в которых дан график, и требуется найти его аналитическое выражение (формулу). Решить графическо-аналитическую задачу значит перейти от графического задания функции к аналитическому. Кармакова Т.С., Табачук Н.П. ХКЗФМШ – 2011/12 Графическо-аналитические задачи направлены на отработку умений по заданному графику (графикам) находить соответствующую формулу (формулы) функций как основных элементарных, так и кусочно-заданных или полученных в результате последовательной деформации исходной элементарной. Задача 6. По заданному графику выбрать формулу кусочно-заданной функции из числа представленных вариантов ответов. ( х 2) 2 , х 2; 1) f(x)= ( х 1) 2 1, х 2. ; ( x 2) 2 , x 2; 2) g(x)= ; ( х 1) 2 1, x 2. х 2 2, х 2; 3) h(x)= ; ( х 1) 2 1, x 2. х 2 , х 0; 4) p(x)= . ( х 1) 2 1, x 0. Решение: 1) Анализируя заданный график, заметим, что он представляет график кусочно-заданной функции, судя по всему это графики двух парабол, одна из которых задана на промежутке x 2, другая на промежутке x<2. 2) При x<2 видим, что ветви параболы y1=а1(x-x0)2+y0 направлены вниз, следовательно, a1<0. Используя график, можно заметить, что вершина параболы находится в точке (1;1), следовательно, х0=1, у0=1, а=-1, т.е. у1=-(х-1)2+1. 3) Аналогично, рассуждая, при х 2, отметим, что ветви параболы y2=а2(xx0)2+y0 направлены вверх, следовательно, a2>0, а вершина параболы находится в точке (2;0), отсюда следует, что х0=2, у0=0, а2=1. Тогда у2=(х-2)2. ( х 2) 2 , х 0; Тогда y= . Следовательно, ответ №1. ( х 1) 2 1, х 2. Задача 7. Задайте аналитически функцию, график которой изображен на рисунке. Хабаровск - 2011 Математика – 9: Задачи на графиках в курсе математики основной школы Решение: 1) Анализируя заданный график, замечаем, что он представляет совокупность двух лучей, т.е. состоит из графиков двух линейных функций, причем одна задана на промежутке х<3, другая на промежутке х 3. 2) При х<3, линейная функция y=k1x+b1 возрастает, значит k1>0, причем b1=2, т.е. y=k1x+2. Найдем k1 c помощью какой-нибудь контрольной точки графика, например, 2 3 (-3;0). Получаем 0= k1 (-3)+2 k1= . 3) Аналогично, рассуждая, отметим, что y=k2x+b2 убывает k2<0, кроме того, 0 k 2 5 b2 . Отсюда следует, что k2=-2, 4 k 2 3 b2 графику принадлежат точки (5;0) и (3;4) b=10. 2 х 2, х 3; Ответ: f(x)= 3 2 x 10, x 3. Под графическо-графической задачей будем понимать задачу, в которой дан график функции и требуется построить на его основе график некоторой другой функции. Будем считать, что решить графическо-графическую задачу значит перейти от графика данной функции к графику другой функции с помощью некоторых преобразований. Задача 8. Зная график функции у=х2, постройте график функции у=(х-2)2+3. Решение: 1.Построим график исходной функции у=х2; 2.Выполним перенос осей координат в точку O’ (2;3); 3.В новой системе координат построим график функции y'=(x’)2. Кармакова Т.С., Табачук Н.П. ХКЗФМШ – 2011/12 Задача 9. На рисунке изображен график функции y=f(x). Постройте: а) у=f(x)+2; б) y=-2f(x); в) y=f(2x); г) y=f(0,5x-1)+2, Решение: а) Осуществили перенос начала координат в точку O'(0;2) и построили в системе x'O'y' график функции y'=f(x’), который будет искомым. Хабаровск - 2011 Математика – 9: Задачи на графиках в курсе математики основной школы б) Осуществили растяжение данного графика вдоль оси ординат в 2 раза и зеркальное отображение вдоль оси Оу. в) Cжали данный график в 2 раза вдоль оси Ох. г) Построим график по следующим шагам: 1)y=f(0,5x) растяжением графика функции y=f(x) в 2 раза вдоль оси Ох; 2)Построенный график перенесем параллельно оси абсцисс на 2 единицы вправо и вверх вдоль оси Оу на 2 единицы (или перенесем начало координат в точку О'(2;2)). Другие задачи на графиках Решение уравнений Будем рассматривать графическое решение уравнений двух видов f(x)=0…(1) и g(x)=h(x)…(2) Кармакова Т.С., Табачук Н.П. ХКЗФМШ – 2011/12 Решить уравнение f(x)=0 – это значит найти такие значения х, при которых функция y=f(x) принимает нулевые значения. Следовательно, чтобы решить уравнение f(x)=0 графически, необходимо: 1) построить график функции y=f(x); 2) найти абсциссы точек пересечения графика функции y=f(x) с осью Ох или точек касания графика с осью Ох; 3) записать ответ. Решить уравнение вида g(x)=h(x) графически, это значит найти такие значения х, при которых значения функции y=g(x) и y=h(x) совпадают. Следовательно, чтобы решить уравнение g(x)=h(x), необходимо: 1) построить графики функций y=f(x) и y=g(x) в одной системе координат; 2) найти абсциссы точек пересечения этих графиков; 3) записать ответ. Задача 10. Используя графики функций у= х 3 и у=2х+4, решите уравнение х3-2х-4=0. Решение: 1)Используя графики функций у= х 3 и у=2х+4, видим, что графики пересекаются в одной точке с координатами (2;8). Абсцисса точки пересечения х=2; 2)Запишем ответ: х=2. Решение систем уравнений Будем рассматривать графическое решение системы уравнений. Решить систему уравнений с двумя переменными, это значит построить в одной системе координат графики уравнений и найти координаты точек пересечения этих графиков. Выделим два типа задач: I Пользуясь рисунком, решите систему уравнений; II На рисунке изображены графики функций, укажите систему уравнений, которая имеет решение (не имеет решение, одно решение, два решения и т.д.). Хабаровск - 2011 Математика – 9: Задачи на графиках в курсе математики основной школы Задача 11. На рисунке изображена парабола и три прямые. Укажите систему уравнений, которая не имеет решений. у х2 1 ; х у 3 1) у х2 1 ; х 5 0 2) у х2 1 3) ; у 6 4) Все три указанные системы уравнений. Решение: 1)Анализируя задание, можно сделать вывод, что графики функций не пересекаются; 2)Пользуясь рисунком, видим, что данному условию удовлетворяет система №1. 3)Запишем ответ: №1 Задача 12. Решить неравенство 1 1 х 3> графически. 2 х 1 Решение: 1 2 1)Построим графики функций у= х 3 и у= 1 в х 1 одной системе координат. 2)Найдем промежутки на оси абсцисс, где график 1 2 функции у= х 3 лежит выше графика функции у= 1 . Видим, что х (-6,2;-1) ( 0,6; ). х 1 3)Запишем ответ: (-6,2;-1) ( 0,6; ). Кармакова Т.С., Табачук Н.П. ХКЗФМШ – 2011/12 Задачи для самостоятельного решения Предлагаемые здесь задачи являются контрольной работой №1 для учащихся 9 классов. Решите эти задачи, запишите решения в отдельную (от физики и информатики) тетрадь. Укажите на обложке следующую информацию о себе: 1. Фамилия, имя, класс, профиль класса (например: Пупкин Василий,9 кл., математический) 2. Индекс, адрес места жительства, электронная почта (если есть), телефон (домашний или мобильный) 3. Данные о школе (например: МБОУ №1 п. Бикин) 4. Фамилия, И. О. учителя математики (например: учитель математики Петрова М.И.) М 9.1.1 Даны свойства функции: а) Область определения функции есть промежуток [-2;7]; б) Значения функции составляют промежуток [-4;4]; в) f(x)<0 в интервалах (0;2) (2;5); г) Нули функции равны 0, 2, 5; д) Наименьшее значение функции равно -4. Укажите график функции, обладающей данными свойствами. 1) 2) 3) 4) Хабаровск - 2011 Математика – 9: Задачи на графиках в курсе математики основной школы М 9.1.2 Выполните задания с изображенными на рисунке графиками функций и номер соответствующего ответу графика зафиксируйте в таблице: № задания 1 2 3 4 5 6 7 8 9 10 № ответа 1) 2) 3) 4) Задание 1: Укажите рисунок, на котором нулем функции является х=0, а область определения функции – промежуток [0;+∞). Задание 2: Укажите рисунок, на котором множеством значений функции является промежуток (-∞;+∞), и изображен график нечетной функции. Задание 3: Укажите рисунок, на котором функция возрастает на промежутке [0;+ ∞), и изображен график функции, которая является ни четной, ни нечетной. Задание 4: Укажите рисунок, на котором областью определения функции является промежуток (-∞;+∞), и функция возрастает на промежутке (-∞;+∞). Задание 5: На каком рисунке изображен график функции, обладающей свойствами: f(0)=3, функция принимает положительные значения в промежутке (-3;3). Задание 6: На каком рисунке изображен график функции, обладающей свойствами: функция является нечетной и нулем функции является х=0. Задание 7: На каком рисунке изображен график функции, обладающей свойствами: f(1)<f(4) и функция принимает положительные значения в промежутке (0;+∞). Кармакова Т.С., Табачук Н.П. ХКЗФМШ – 2011/12 Задание 8: Укажите рисунок, на котором областью определения функции является промежуток (-∞;+∞), а наибольшее значение функции равно 3. Задание 9: На каком рисунке изображен график функции, обладающей свойствами: f(1)>f(-2) и f(2)=0. Задание 10: Укажите рисунок, на котором нулем функции является х=0, а функция возрастает на промежутке [0;+∞). М 9.1.3 На рисунке изображены графики функций вида y=kx+b. Установите соответствие между графиками и знаками коэффициентов k и b. a) k>0, b<0; 1) b) k<0, b>0; 2) c) k<0, b<0; 3) d) k>0, b>0. 4) М 9.1.4 Выберите функцию, график которой изображен на рисунке. 1 1 2 х , | x | 1 1) f(x)= 2 2 ; 2 x 1, | x | 1 х 2 1, | x | 1 2) f(x)= 1 2 1 ; x , | x | 1 2 2 1 2 1 х , | x | 1 3) f(x)= 2 ; 2 x 2 1, | x | 1 2 1 х , | x | 1 4) f(x)= . 2 x 2 1, | x | 1 М 9.1.5 На рисунке изображены пары графиков. В каждой паре один из графиков принадлежит функции y=f(x). Задайте вторую функцию. Хабаровск - 2011 Математика – 9: Задачи на графиках в курсе математики основной школы а) б) в) г) д) е) Кармакова Т.С., Табачук Н.П.