20111206095730!Открытый_урок

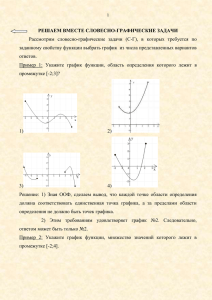
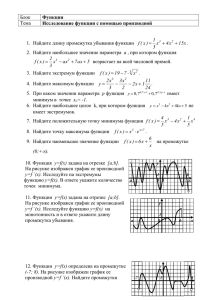
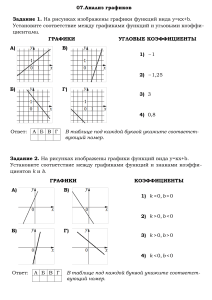
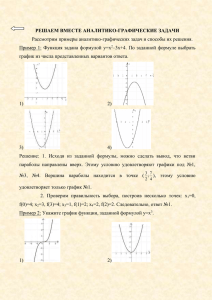
Повторительно-обобщающий урок на тему:
«Числовые функции»
1. Тип урока: комбинированный; содержит следующие учебно-воспитательные
дидактические моменты: организационный момент, этап проверки домашнего задания,
устная работа, закрепление темы, этап проверки усвоения знаний в виде игры-эстафеты,
итог урока.
2. Цели урока:



систематизировать и обобщить знания о свойствах функции, развивать навыки
построения и прочтения графиков функций, умение работать с тестовыми
заданиями;
развивать логическое мышление, умение делать обобщения и выводы;
воспитывать сознательное отношение к учебе, познавательную активность.
3. Актуальность:


задания по данной теме встречаются в тестах единого государственного экзамена
по математике в 9 классе (в новой форме) и 11 классе;
чтение графиков функций имеет большое практическое значение.
4. Ход урока:
Организационный момент
1. Приветствие.
2. Проверка наличия отсутствующих.
I Проверка домашнего задания (двое учащихся у доски комментируют решение
домашнего задания).
№ 295 (г) - исследовать на четность
y(x) = x2 +8/x-9
y(-x) = (-x)2+9/(-x)2-9 = x2+8/x2-9
y(-x) = y(x) y = x2+8/x2-9 – четная
Сообщение темы:
- Ребята, сегодня мы обобщим и закрепим знания по теме: “Свойства числовых
функций”, проведем самодиагностику, где вы проверите уровень ваших знаний. Эти
знания помогут вам при сдаче экзаменов за 9 кл. и ЕГЭ.
II Фронтальная устная работа
1. По данным рисункам определите, какие из функций
- нечетные
- четные
2. Какая из перечисленных функций изображена на графике:
а) Y=|x|-1
б)Y=|x-1|+1
в) Y=|x+1|-1
г) Y=|2x|
3. Укажите Д(у) и Е(у)
Д(у)=[-3;5)
E(y)=[-1;4]
4. Укажите число целых значений
функции:1) 2
2) 3
3) 4 4) 5
5. Укажите сумму целых значений функции:
1) –2
3) 1
2) 0
4) 2
6. Найдите область определения функций:
Y=2x+1/x(x+1)
Y=19x-12/(5x-4)(x-13)
Y= x2+13
Y= 1/ 11-x
III Повторение по теме «Свойства числовых функций»
Работа с задачником Мордковича А.Г. стр. 73, №298
(Вызов одного учащегося к доске)
Задание: Функция задана кусочно. Начертите график и опешите свойства.
Решение:
1
-2<x<-1
2
У=
2х -1
-1<x<1
1
1<x<2
1. у=1, часть прямой на отрезке [-2;-1]
2. у=2х2-1 парабола на полуинтервале (-1;1]
х -1 0 1
у 1 -1 1
3. у=1, часть прямой на полуинтервале (1;2]
Свойства:
1. Д (у)=[-2;2]
2. Функция четная
3. Функция возрастает на отрезке [0;1], убывает на отрезке [-1;0], постоянная на
[1;2]
4. Ограниченная прямой у=-1
5. У наим.= -1
У наиб.= 1
6. непрерывная
7. Е (у) = [-1;1]
8. На отрезке [-1;1] выпукла вниз.
IV Один учащийся записывает ответы на доске, остальные в тетради.
1. Найдите область определения функции, изображенной на рис.1.
[-2;-1],
1) [-1;3]
2) [0;6]
3) [-2;6]
4) [0;3]
2. Найдите область значения функции, изображенной на рис.1.
1) [-1;3]
2) [0;6]
3) [-2;6]
4) [0;3]
3. По графику функции у = f(x), изображенном на рис.1, найдите нули функции.
1) 1
2) 1;1
3) 1;4
4) 4
4. На одном из рисунков изображен график функции, возрастающей на промежутке [0;2].
Укажите этот рисунок.
5. На одном из рисунков изображен график функции, убывающей на промежутке [3;7].
Укажите этот рисунок.
6. На рисунке изображен график функции у = f(x). Из приведенных утверждений выберите
верное.
f(-1) < f(2)
функция у = f(x) убывает на промежутке (- ;3]
f(0) = 2
функция принимает наименьшее значение при х =1.
7. Используя график функции у = f(x), определить, какое утверждение верно:
1) f(3) > f(2)
2) функция у = f(x) возрастает на промежутке [2;+
)
3) функция принимает наибольшее значение при х = 2
4) f(0) = -1
V Тестовая работа
(В бланке ответов и себе в черновик заносятся результаты теста, затем после сдачи
бланков ответов демонстрируются на доске. Учащиеся проводят самодиагностику.)
1в 2в
1г 1б
2б 2а
3а 3б
4г 4а
5в 5г
6б 6в
Подводим итоги: кто верно выполнил 7 заданий у кого 1 ошибка у кого 2 ошибки - Ребята, окончательные итоги подведу я.
VI Групповая работа (Раздаются карточки группам)
- работают 6 групп, где 1 пара групп получает одно задание
- проверим, кто верно и быстро задаст аналитически функцию по графику:
1. у = |x-2|+2
у
у
2
х х<0
2.
0
1 2
х
х
у=
1
у
х
2
2
3.
0
x>0
x +1
x<1
2
x>1
2
0 1
х
Y=
Затем от группы один лидер записывает и комментирует решение на доске, а другая
группа проверяет.
VII Итоги урока:
- Оцениваются теоретические и практические знания по данной теме всего класса и
отдельных учащихся
- Подводится итог изучения раздела «Числовые функции» и еще раз сообщается важность
и необходимость обобщения этого понятия
VIII. Домашнее задание
№289, №311 стр. 75 (из учебника с опережением).