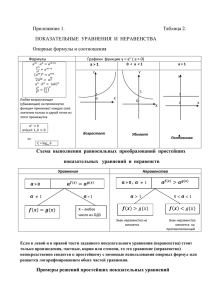
Способы решения показательных уравнений

Способы решения показательных уравнений.
1. Приведение двух частей уравнения к одному основанию, тогда
если
ах=а у,
то х = у.
х
х
х
помним : а ·в =(а·в) ;
1
ах
= а-х
ах
а
х
х у
х+у
=
(
)
;
а
·а
=
а
;
х
в
в
ах:ау= ах- у; (ах)у= аху;
и если число представлено десятичной дробью, то будет проще, если
заменить его обыкновенной.
2. Введение новой переменной.
а) основания одинаковые, но степени отличаются в n раз, тогда меньшую
степень обозначаем через а, а большею через аn.( 32х - 2·3х- 3=0; 3х=а;
32х = а2)
б) основания одинаковые, но степени отличаются знаком, тогда
1
положительную степень обозначаем через а, а отрицательную через ; ( 3 х
а
1
+ 2·3- х- 3=0; 3х=а; 3-х= ) и приводим все к общему знаменателю.
а
Помним: иногда для приведения к таким степеням бывает необходимо применение
формул для разложения суммы или разности степеней. ах+у
= ах·ау;
ах- у = ах:ау;
3. Разложение на множители.
а) вынесением за скобки наименьшей степени.
3· 2х+3 - 2х+4 =4
2х+3 (3 – 2) =4 …
Помним: можно выносить множитель при условии, что коэффициент при
переменной одинаковый
б) группировки или по ФСУ.
Пример №1
5х+5х+1+5х+2 = 3х+3х+1+3х+3
5х (1+5+25) = 3х (1+3+27)
5х · 31 = 3х ·31
5х = 3х значит х = 0
Помним: Если получается Ах = Вх, то х=0; Если получается Ах · Ву = Аn · Вm, то
х=n
у=m
2 х
пример №2
х ·3 +9 – 3х = 9х2
х2 (3х – 9) - (3х – 9) =0
( х2 - 1)(3х – 9) = 0
( х2 - 1) = 0 или (3х – 9) = 0
4 Если показатель представлен дробью с переменной, то вероятно надо
выделить целые части и представить показатели в виде суммы.
5. . Симметрические уравнения. А а 2х + В (а · в) х + С в 2х = 0
(делим на в 2х )
4·22х – 6х = 18· 32х ( :32х )
2
2
2
4·( )2х – ( )х =18. Затем вводим новую переменную ( )х = а …
3
3
3
6. Если произведение оснований равно1, а показатели равны между собой,
то вводим переменную, обозначая одно через t, а другое через 1/t.
а х в х = (а в ) х = 1 а х = 1/ в х ( особенно, если основания
иррациональные выражения типа √5 ± 2)
(4+√15)х + (4-√15)х = 62
а+
1
а
1
так как (4+√15)·(4-√15) = 1, то (4+√15)х = а, (4-√15)х = а
= 62 …
7. Функциональный способ: каждая часть представлена функцией разной
монотонности. Одна точка пересечения. Находим х подбором.
4х +3х=7 (слева возрастающие функции, а справа постоянная, у них одна точка
пересечения, которую находим подбором. Х=1)
8. Уравнения с переменным основанием и показателем:
Рассматриваем несколько случаев: а) основание равно 1.
б) основание равно 0; (в этом случае делаем проверку. Не имеет смысла
0
0 и 0 в отрицательной степени) в) основание равно ( - 1) , в этом случае
делаем проверку) г) приравниваем показатели.
(х + 5)2х- 1 = (х+5) 4 - х
9. Если основания степеней образуют геометрическую прогрессию, то
делим на большую степень и вводим новую переменную.
10 Логарифмирование
2х = 3
log 2 2х = log 2 3
х = log 2 3
Решение показательных неравенств.
1. Приведение неравенства к виду
ах<а
у
тогда
 Если основание больше 1, то знак неравенства остается прежним.
 Если основание больше 0, но меньше 1, то знак неравенства меняется
на противоположный.
2. Метод интервалов при решении показательных неравенств
1. Введение функции
2. Найти область определения этой функции.
3. Найти нули этой функции
4. Нанести на прямую полученные значения и определить знаки
функции. Выбрать нужные интервалы
5. Совместить П2 и П4, найти общее решение