3 - slepenkova.ru
реклама
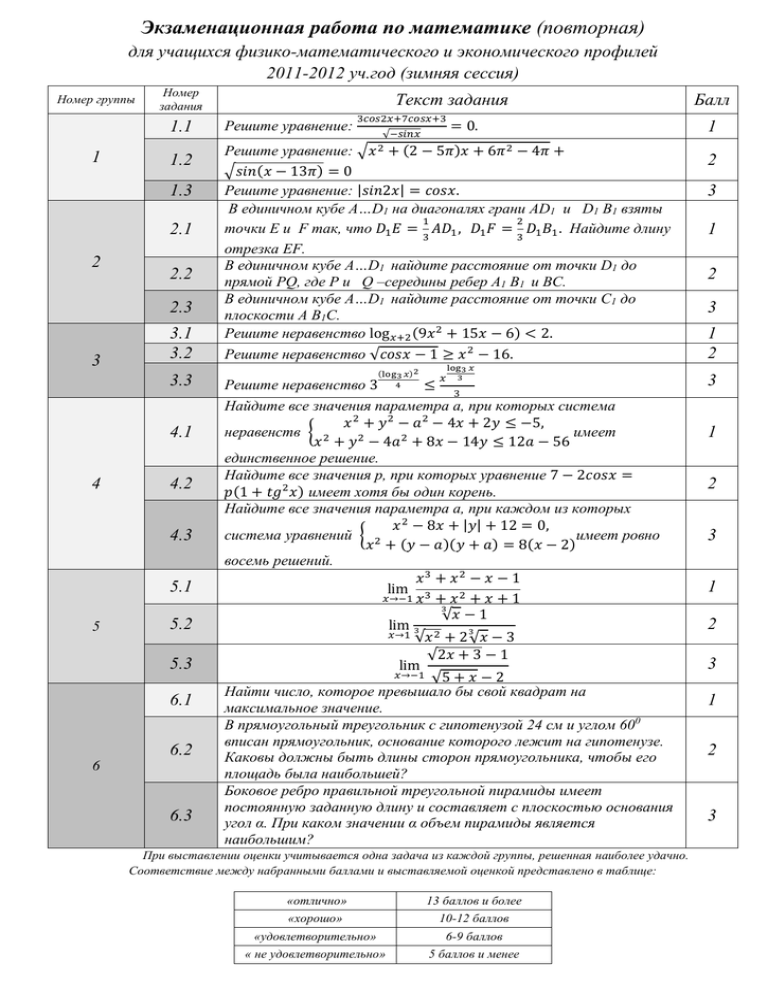
Экзаменационная работа по математике (повторная)
для учащихся физико-математического и экономического профилей
2011-2012 уч.год (зимняя сессия)
Номер группы
Номер
задания
1.1
1
1.2
1.3
2.1
2
2.2
2.3
3
3.1
3.2
3.3
4.1
4
4.2
4.3
5.1
5
5.2
5.3
6.1
6.2
6
6.3
Текст задания
Решите уравнение:
3𝑐𝑜𝑠2𝑥+7𝑐𝑜𝑠𝑥+3
√−𝑠𝑖𝑛𝑥
√𝑥 2 + (2 −
= 0.
Решите уравнение:
5𝜋)𝑥 + 6𝜋 2 − 4𝜋 +
√𝑠𝑖𝑛(𝑥 − 13𝜋) = 0
Решите уравнение: |𝑠𝑖𝑛2𝑥| = 𝑐𝑜𝑠𝑥.
В единичном кубе A…D1 на диагоналях грани AD1 и D1 B1 взяты
1
2
точки Е и F так, что 𝐷1 𝐸 = 3 𝐴𝐷1 , 𝐷1 𝐹 = 3 𝐷1 𝐵1 . Найдите длину
отрезка EF.
В единичном кубе A…D1 найдите расстояние от точки D1 до
прямой PQ, где P и Q –середины ребер А1 B1 и ВС.
В единичном кубе A…D1 найдите расстояние от точки С1 до
плоскости А B1С.
Решите неравенство log 𝑥+2 (9𝑥 2 + 15𝑥 − 6) < 2.
Решите неравенство √𝑐𝑜𝑠𝑥 − 1 ≥ 𝑥 2 − 16.
(log3 𝑥)2
4
𝑥
log3 𝑥
3
Решите неравенство 3
≤ 3
Найдите все значения параметра а, при которых система
𝑥 2 + 𝑦 2 − 𝑎2 − 4𝑥 + 2𝑦 ≤ −5,
неравенств { 2
имеет
𝑥 + 𝑦 2 − 4𝑎2 + 8𝑥 − 14𝑦 ≤ 12𝑎 − 56
единственное решение.
Найдите все значения р, при которых уравнение 7 − 2𝑐𝑜𝑠𝑥 =
𝑝(1 + 𝑡𝑔2 𝑥) имеет хотя бы один корень.
Найдите все значения параметра а, при каждом из которых
𝑥 2 − 8𝑥 + |𝑦| + 12 = 0,
система уравнений { 2
имеет ровно
𝑥 + (𝑦 − 𝑎)(𝑦 + 𝑎) = 8(𝑥 − 2)
восемь решений.
𝑥3 + 𝑥2 − 𝑥 − 1
lim 3
𝑥→−1 𝑥 + 𝑥 2 + 𝑥 + 1
3
√𝑥 − 1
lim 3
𝑥→1 √𝑥 2 + 2 3√𝑥 − 3
√2𝑥 + 3 − 1
lim
𝑥→−1 √5 + 𝑥 − 2
Найти число, которое превышало бы свой квадрат на
максимальное значение.
В прямоугольный треугольник с гипотенузой 24 см и углом 600
вписан прямоугольник, основание которого лежит на гипотенузе.
Каковы должны быть длины сторон прямоугольника, чтобы его
площадь была наибольшей?
Боковое ребро правильной треугольной пирамиды имеет
постоянную заданную длину и составляет с плоскостью основания
угол α. При каком значении α объем пирамиды является
наибольшим?
При выставлении оценки учитывается одна задача из каждой группы, решенная наиболее удачно.
Соответствие между набранными баллами и выставляемой оценкой представлено в таблице:
«отлично»
13 баллов и более
«хорошо»
10-12 баллов
«удовлетворительно»
6-9 баллов
« не удовлетворительно»
5 баллов и менее
Балл
1
2
3
1
2
3
1
2
3
1
2
3
1
2
3
1
2
3











