Лекция 10: мультиколлинеарность и регуляризация Тихонова
реклама
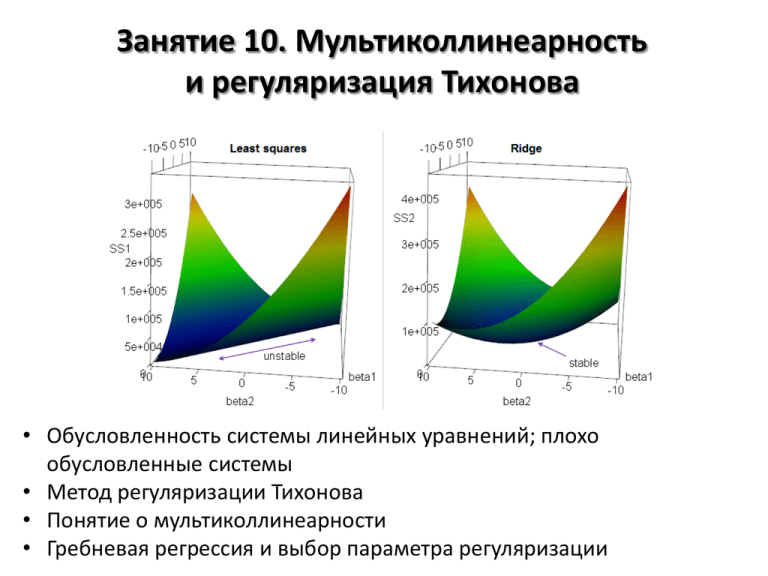
Занятие 10. Мультиколлинеарность и регуляризация Тихонова • Обусловленность системы линейных уравнений; плохо обусловленные системы • Метод регуляризации Тихонова • Понятие о мультиколлинеарности • Гребневая регрессия и выбор параметра регуляризации Обусловленность системы линейных уравнений Хорошо обусловленная Плохо обусловленная Вырожденная Проблемы, связанные с плохо обусловленными задачами • Чувствительность решения к ошибкам в исходных данных • Возможно сильное влияние погрешностей численных расчётов Возможное решение проблемы – регуляризация (привнесение в задачу дополнительной информации о свойствах решения) Метод регуляризации Тихонова Исходная система уравнений 𝐴𝑥 = 𝑦 det 𝐴 ≈ 0 (плохо обусловленная) Регуляризованная система уравнений 𝐴 + 𝜆𝐼 𝑥 = 𝑦 𝜆 > 0 – параметр регуляризации Пример плохо обусловленной системы линейных уравнений и проблем с ее решением Поиск оптимального λ (минимизация функционала Тихонова) 𝑥 + 7𝑦 = 5 Ω 𝜆 = 𝐴𝑥 − 𝑦 2 +𝜆 𝑥 2 2𝑥 + 98𝑦 = 50 >> A = [1 7; 2^0.5 98^0.5]; >> y = [5; 50^0.5]; >> x = inv(A)*y; disp(x’); warning: matrix singular to machine precision 0.60938 1.24121 >> disp((A*x)’) 9.2979 13.1491 >> k = 1e-9; >> x=inv(A+k*eye(2))*y;disp(x); 0.45874 0.64875 >> disp((A*x)’) 5.0000 7.0711 Мультиколлинеарность Мультиколлинеарность – наличие линейной зависимости между объясняющими переменными (факторами) регрессионной модели Графики зависимости факторов друг от друга 𝑦 = 𝛽0 + 𝛽1 𝑥1 + 𝛽2 𝑥2 + 𝛽3 𝑥3 ! ! Гребневая регрессия (Ridge regression) Гребневая регрессия Метод наименьших квадратов ⊤ 𝛽= 𝑋 𝑋 −1 𝛽 = 𝑋 ⊤ 𝑋 + 𝜆𝐼 ⊤ 𝑋 𝑦 𝑦𝑖 − 𝑦𝑖 𝑋 ⊤𝑦 Минимизация функции Минимизация функции 𝑅𝑆𝑆 = −1 𝑅𝑆𝑆 = 2 𝑦𝑖 − 𝑦𝑖 2 𝑖 𝑖 𝛽𝑗2 +𝜆 𝑗 Смещенность оценки 𝜷 𝐸 𝛽 = 𝐸 𝑋 ⊤ 𝑋 + 𝜆𝐼 −1 𝑋 ⊤ 𝑋𝐵 + 𝜀 = 𝑋 ⊤ 𝑋 + 𝜆𝐼 −1 (𝑋 ⊤ 𝑋)𝐵 Дисперсия оценки 𝜷 ⊤ cov 𝛽, 𝛽 = 𝐸 𝑋 ⊤ 𝑋 + 𝜆𝐼 −1 𝑋 ⊤ 𝜀 𝑋 ⊤ 𝑋 + 𝜆𝐼 −1 𝑋 ⊤ 𝜀 = 𝑋 ⊤ 𝑋 + 𝜆𝐼 −1 𝑋 ⊤ 𝐸 𝜀𝜀 ⊤ 𝑋 𝑋 ⊤ 𝑋 + 𝜆𝐼 −1 = 𝜎 2 𝑋 ⊤ 𝑋 + 𝜆𝐼 −1 𝑋 ⊤ 𝑋 𝜎 2 = (𝑒 ⊤ 𝑒)/(𝑛 − 𝑘) - ошибка регрессии Дисперсии 𝛽 - на главной диагонали матрицы 𝑋 ⊤ 𝑋 + 𝜆𝐼 −1 Гребневая регрессия: поверхность функции RSS(β) 𝑦 = 𝛽0 + 𝛽1 𝑥1 + 𝛽2 𝑥2 Обратите внимание: при росте параметра регуляризации эллипсы изолиний вокруг минимума «стягиваются» в окружности λ=0.1 λ=0 λ=1 Гребневая регрессия: стандартизация точек Исходная модель 𝑦𝑖 = 𝛽0 + НО! • Разная размерность у разных 𝛽𝑖 и 𝑥𝑗 • При 𝜆 → ∞ 𝛽0 → 0 (нежелательно) 𝛽𝑗 𝑥𝑖𝑗 𝑗 𝑅𝑆𝑆 = 𝑦𝑖 − 𝑦𝑖 2 𝛽𝑗2 +𝜆 𝑖 Необходимость нормировки 𝑗 Стандартизация (нормировка) исходных данных 𝑦𝑖∗ = 𝑦𝑖 − 𝑦 𝑗 = 𝑦𝑗 − 𝑦 2 𝑦𝑖 − 𝑦 𝑦𝑛𝑜𝑟𝑚 ∗ 𝑥𝑖𝑗 𝑥𝑖𝑗 − 𝑥𝑗 = 𝑘 𝑥𝑘𝑗 − 𝑥𝑗 2 𝑥𝑖𝑗 − 𝑥𝑗 = 𝑥𝑗,𝑛𝑜𝑟𝑚 Переход к исходным размерностям 𝑦𝑖∗ = 𝛽0∗ + 𝛽𝑗∗ 𝑥𝑖𝑗 ⇒ 𝑗 =0 𝑦𝑖 = 𝑦𝑛𝑜𝑟𝑚 𝛽0∗ 𝑦𝑖 − 𝑦 = 𝛽0∗ + 𝑦𝑛𝑜𝑟𝑚 𝛽𝑗∗ 𝑥𝑗 + 𝑦 − 𝑦𝑛𝑜𝑟𝑚 𝑗 𝑥𝑗,𝑛𝑜𝑟𝑚 𝛽𝑗∗ 𝑗 𝑥𝑖𝑗 − 𝑥𝑗 ⇒ 𝑥𝑗,𝑛𝑜𝑟𝑚 + 𝑦𝑛𝑜𝑟𝑚 𝑗 𝛽𝑗∗ 𝑥𝑖𝑗 𝑥𝑗,𝑛𝑜𝑟𝑚 Гребневая регрессия: фактор инфляции дисперсии VIF (Variance Inflation Factor, фактор инфляции дисперсии) – мера мультиколлинеарности, позволяет оценить увеличение дисперсии из-за линейной зависимости фактора 𝑥𝑖 от остальных 𝜎2 𝜎2 1 Var 𝛽𝑗 = 2 𝑉𝐼𝐹𝑗 = 2 2 1 − 𝑅 𝑗 𝑥 − 𝑥 𝑥 − 𝑥 𝑗 𝑗 𝑖 𝑖𝑗 𝑖 𝑖𝑗 𝑅𝑗2 - коэффициент детерминации линейной зависимости фактора 𝑥𝑖 от остальных факторов Возможные значения VIF • VIF > 10 – выраженная мультиколлинеарность • VIF = 5-10 – мультиколлинеарность • VIF = 1-5 – нет мультиколлинеарности Гребневая регрессия: подбор параметра регуляризации Ridge trace plot (график следа гребня) VIF plot (фактор инфляции дисперсии) Оптимальный λ (стабилизация β) Оптимальный λ (VIF=1-5) 𝜎2 Var 𝛽𝑗 = 𝑖 𝑥𝑖𝑗 − 𝑥𝑗 2 𝑉𝐼𝐹𝑗