«Анализ простейших термодинамических процессов (изохорного, изобарного, изотермического и адиабатного).»
реклама

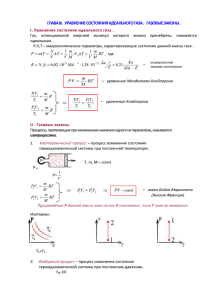
Тема. «Анализ простейших термодинамических процессов (изохорного, изобарного, изотермического и адиабатного).» изучение основных законов идеального газа умение анализировать изопроцессы умение применять их на практике Основные параметры (t),[К ] (Т),[К ] (t),[0С ] Р - [Па] = [Н/м3] Р - [Па] = [Н/м2] υ = V / m , [м2/кг] υ = V / m , [м3/кг] Pυ=RT R = 8314,20 Дж/моль R = 8314,20 Дж/кг·К Понятия и определения термодинамики. Функции состояния U [Дж] u [Дж/кг] H [Дж] h [дж/кг] S [Дж/К] s [Дж/кгК] Внутренняя энергия – вся энергия, заключенная в теле или системе тел. Удельная внутренняя энергия. Энтальпия характеризуется суммой внутренней энергии. Удельная энтальпия-отношение полной энтальпии к массе тела. Энтропия характеризует состояние рабочего тела. Удельная энтропия. Понятия и определения термодинамики. Функции процесса Работа Удельная работа L [Дж] l [Дж/кг] Q [Дж] q [Дж/кг] Теплота Удельная теплота Состояние тел Состояние 1 1 p1,v1,T1 Основные термодинамические процессы Изохорный процесс подвода и отвода теплоты при постоянном объеме (V=const); Изобарный процесс сообщения или отнятия теплоты при постоянном давлении (p=const) Изотермический процесс, протекающий при постоянной температуре (Т=const) Адиабатный процесс, без сообщения или отнятия теплоты извне (dq=0) Задачи исследования термодинамических процессов выводится уравнение процесса, которое устанавливает связь между начальными и конечными параметрами; вычисляется работа изменения объема газа; определяется количество теплоты, подведенной или отведенной к газу в процессе; определяется величина изменения внутренней энергии системы; устанавливается изменение энтропии рабочего тела. Процессы Состояние 2 2 Процесс 1-2 Состояние 1 1 p2,v2,T2 Изохорный процесс (V=const) 2 Изохора (вертикаль) 1 Изохорный процесс v = Const , v 2 = v 1 Уравнение состояния процесса: P2 / P1 = T2 / T1 Так как υ 2 = υ 1, то l = 0 и уравнение 1-го закона т/д: q = Δu = сv·(t2 - t1) Для М кг газа Q=M·q= ΔU Изменение энтропии S2–S1 = Cv·ln P2/P1=Cv·ln T2/T1 Закон Шарля При постоянном объеме изменение давления прямо пропорционально изменению температуры P P 1 2 T T 1 2 Газ находится в запаянном сосуде, Тест 1 температура газа меняется так, как показано на рисунке. Какой из графиков отражает изменение давления этого газа с течением времени? Изобарный процесс (P=const) Изобара 1 (горизонталь) 2 Изобарный процесс P = Const , P2 = P1 Уравнение состояния процесса: v 2 /v 1 = T2 / T1 Работа этого процесса: l = P·(v 2 -v1) Уравнение 1-го закона т/д : q = Δu + l = ср·(t2 - t1) Для М кг газа Qp =M · qp Изменение энтропии S2–S1 = ср·ln ·T2/T1 Закон Гей - Люсака При постоянном давлении изменение объема прямо пропорционально изменению температуры V V 1 2 T T 1 2 В ходе изобарного процесса абсолютная температура Тест 2 увеличилась в 2 раза. Как изменился объем газа? 1 Не изменился. 2 Уменьшился в 2 раза. 3 Увеличился в 2 раза. 4 Уменьшился в 4 раза. 5 Увеличился в 4 раза. Изотермический процесс (Т=const) 1 Изотерма (гипербола) 2 Изотермический процесс Т = Const , Т2 = Т1 Уравнение состояния: P1 / P2 = v 2 / v 1 Так как Т2 = Т1, то Δu = 0 Уравнение 1-го закона т/д q = l = R·T·ln(v 2/v 1) или q = l = R·T·ln(P1/P2) Для М кг газа L=M·l Изменение энтропии S2–S1 = R·ln ·v2/v1 Закон Бойля - Мариотта При постоянной температуре произведение давления на объем есть величина постоянная p V p V 1 1 2 2 Адиабатный процесс q =0 Уравнение состояния: P· v k = Const k = cp / cv – показатель адиабаты Уравнение 1-го закона т/д l=-Δu=-сv·(t2 – t1)=сv·(t1 – t2) l = R·(T1 – T2) / (k -1) l = R·(p1v1 – p2v2) / (k -1) Энтропия не изменяется S2=S1 =S=const На рисунке представленТест график3зависимости давления газа от его объема. Каким должно быть давление газа при его сжатии до объема V = 2 м3, если обнаруженная зависимость сохраниться? Процесс 1 - m – изотермический . Т 1 Tm Закон p1V1 pmVm pV . Vm 1 1 p pm . Процесс m - 2 – изобарный . рm р 2 Vm Т m Закон V Т2 V2Т m 2 Vm Т2 p1V1 V2Т m pm Т2 p1V1 V2Т 1 p2 Т2 p1V1 p2V2 Т1 Т2 m 1 2 V pV const Т Задачи 1 группа: Задача: в закрытом резервуаре емкостью 2м3 содержится воздух при абсолютном давлении 0.5 МПа и температуре 270С. Нужно найти абсолютное давление и температуру газа в резервуаре после подвода к воздуху 300кДж теплоты. 2 группа: Задача: азот в количестве 10 кг охлаждается от температуры t1=4000С до температуры t2=1000С при постоянном давлении 0,1 МПа. Требуется найти количество отводимой теплоты и работу в процессе. 3 группа: Задача: диоксид углерода СО2 занимает объем 5м3 при давлении 0,5 МПа. В процессе изотермного расширения давление снизилось до 0,1 МПа. Требуется найти работу и количество теплоты в процессе. 4 группа: Задача: в газовом двигателе смесь газа и воздуха адиабатно сжимается так,что к концу сжатия ее температура оказывается на 2000С ниже температуры самовоспламенения газа. Давление в начале сжатия 0,09 МПа и начальная температура 700С. Показатель адиабаты 1,36, газовая постоянная 314 Дж/(кгК), температура самовоспламенеия равна 6500С. Определить величину работы сжатия. Ответы на задачи 1 задача: Ответ: Т2=336,04 К; р2=0,56 МПа. 2 задача: Ответ: Q=-3117.8кДж; L=-891,0 кДж. 3 задача: Ответ: Q=L=4024 кДж. 4 задача: Ответ: L=-331,4 кДж/кг.