Вычисление определённого интеграла по формулам
реклама

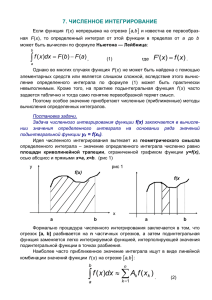
Мелков Владислав, 2Л21 МЕТОД ПРЯМОУГОЛЬНИКОВ. Геометрически идея способа вычисления определённого интеграла по формуле прямоугольников состоит в том, что площадь под графиком интегральной функции заменяется суммой площадей прямоугольников, одна сторона которых равна , а другая - . ПЛОЩАДЬ С НЕДОСТАТКОМ. ПЛОЩАДЬ С ИЗБЫТКОМ. АЛГОРИТМ ВЫЧИСЛЕНИЯ. Чтобы найти приближённое значение интеграла , нужно: 1. разделить отрезок интегрирования [a, b] на n равных частей точками х0= а, х1, х2,..., х n -1, х n = b ; 2. вычислить значения подынтегральной функции в точках деления, т.е. найти у 0 = f (x0), у 1 = f (x1), у 2 = f (x2), у n -1 = f (xn-1), у n = f (xn) ; 3. воспользоваться одной из приближённых формул. 4. Для того, чтобы найти погрешность вычислений, надо воспользоваться формулами: , МЕТОД ТРАПЕЦИЙ В этом методе отрезок [a; b] так же разбивается на n-равных частей. На каждом отрезке [xi; xi+1] кривая y = f(x) заменяется прямой, проходящей через две известные точки с координатами и . где и строится прямоугольная трапеция с высотой . , МЕТОД ТРАПЕЦИЙ. АЛГОРИТМ ВЫЧИСЛЕНИЯ. Рассмотрим определенный интеграл , где – функция, непрерывная на отрезке . Проведём разбиение отрезка на равных отрезков: . При этом, очевидно: (нижний предел интегрирования) и (верхний предел интегрирования). Точки также называют узлами. Тогда определенный интеграл можно вычислить приближенно по формуле трапеций: ,где – длина каждого из маленьких отрезков или шаг; – значения подынтегральной функции в точках . ПРИМЕР. Задние:Вычислить приближенно определенный интеграл по формуле трапеций. Разбив отрезок интегрирования на 3 части. Результаты округлить до трёх знаков после запятой. РЕШЕНИЕ. Спасибо за внимание!