Понятие функции Открытый урок 9 класс 2014 год

Понятие функции
Открытый урок 9 класс
2014 год
Устный счёт-разминка
Решить неравенства
2х  7  0
( х  2)( х  7)  0
х 1  0
2
х( х  2) ( х  7)
0
( х  3)
2
2
Бытовое определение функции
Пусть даны множества Х и У. Если
каждому элементу х из Х по
некоторому правилу F поставить в
соответствие один и только один
элемент у из множества У, то
говорят, что задана функциональная
зависимость
у=F(x)
3
Математическое определение
функции
Функцией называется однозначное
соответствие между двумя непустыми
множествами (Х и У), при котором
каждому элементу множества Х ставится
в соответствие элемент из множества У.
х – аргумент (независимая переменная)
у – функция (зависимая переменная)
Х- область определения функции D(f(x))
У- область значений функции E(f(x))
4
5
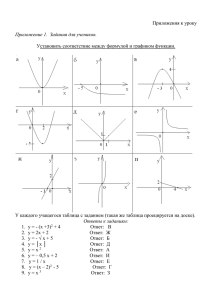
Какие из данных графиков являются
графиками каких-либо функций?
6

Область определения функции – это
множество, на котором задаётся
функция.

Область значений – это множество
всех значений, которые может
принимать данная функция.
7
1. Укажите область определения функций
х 1
у
( х  2)( х  3)
у  х  3х  4
2
у
х
х2
D( f ) : x   2; x  3
D( f )  (;  )
D( f )    ; 0 2;  
8
2. Для каждого графика укажите D(f) и E(f):
D( f )   3; 1
E ( f )   2; 4
D( f )   3; 2 D( f )   4;  2 1; 3
E ( f )  {2}  {2}.
E ( f )  1; 5
9
3. Верно ли, что D(f) = E(f) ?
у  х2
1
у
х
D ( f )  (  ;  )
E ( f )  0 ;  
D( f )  ( ; 0)  (0;  )
E ( f )  ( ; 0)  (0;  )
10
4. Верно ли, что D(f) = E(f) ?
у х
D ( f )  (  ;  )
E ( f )  0 ;  
у х
D ( f )  0 ;   
E ( f )  0 ;   
11
Задание №1

a.
b.
c.
Определите D(f) и E(f) для следующих
функций:
f(x)=
f(x)=
f(x)=
Ответы запишите в бланк.
12
Что значит задать функцию?
Указать правило, которое
позволяет произвольно
выбранному значению х из
D(f) сопоставить значение у
из E(f).
13
Способы задания функции
 Словесное описание
 Формула
 Таблица
 График
14
Задание функции с помощью
словесного описания
Каждому числу, меньшему 5, ставится
в соответствие 1, а каждому числу, не
меньшему 5, ставится в соответствие – 1.
Задание № 2
Изобразить график и доказать, что эта
зависимость является функцией.
15
Задание функции с помощью формулы
Задание №3
F(x) =
Определить вид функции и
построить её график
16
Табличный способ задания функции.
Задание № 4
По данной таблице в листе ответов построить
график функции и определить её вид
Х -4 -3 -2 -1 0
У 13 6
1
1
2
-2 -3 -2 1
3
6
4
13
17
Графический способ задания
функции
Графиком функции F(x)
называется множество точек
координатной плоскости (х, F(x)).
18
Задание №5
Пользуясь шаблоном графика
функции y=x2 , построить график
функции f(x)=
. Определить
сколько общих точек будет иметь с
графиком функции прямая у=2.
19
Найдите
соответствия:
у  х 5
2
у  0,3х
2
у  ( х  3)
2
у   х  2   5
2
20
Спасибо за урок!
21