Лекция 13. Энергия магнитного поля. Уравнения Максвелла © Музыченко Я.Б., 2011
реклама
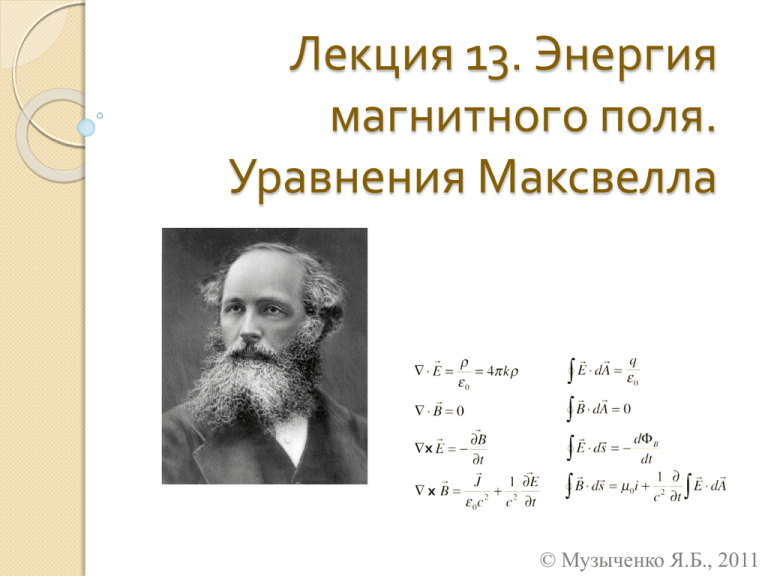
Лекция 13. Энергия магнитного поля. Уравнения Максвелла © Музыченко Я.Б., 2011 Энергия контура с током При замыкании цепи ток будет постепенно убывать. Работа, совершенная эти током за время dt: dA s Idt где d s , LI, следовательно dt dA LIdI - дополнительная работа сторонних сил, совершаемая против ЭДС самоиндукции. 2 LI A LIdI 2 2 2 Энергия контура с током Магнитное поле является носителем энергии, за счет которой совершается работа. Собственная энергия тока: 2 2 LI I W 2 2 2L Энергия соленоида: 2 2 2 2 LI 0n VI 0 H V W 2 2 2 3 3 Энергия магнитного поля Для однородного магнитного поля 2 2 0 H V B V BHV W 2 20 2 Для произвольного магнитного поля: W dV 0 H B BH 2 20 2 2 4 2 3 [] Дж / м - объемная плотность энергии магнитного 4 поля Магнитная энергия двух контуров с током Рассмотрим два неподвижных контура. При замыкании каждого из контуров возникает ЭДС индукции и ЭДС взаимной индукции. 2 2 L1I1 L2 I 2 W L12 I1I 2 2 2 собственная взаимная энергия энергия контуров контуров с током с током Взаимная энергия – величина алгебраическая, знак зависит от направления токов в контурах. 5 5 Уравнения Максвелла -система дифференциальных уравнений, описывающих электромагнитное поле. Математическое завершение теории электромагнетизма, начатой Эрстедом, Ампером, Генри, Фарадеем. Основные идеи: - меняющееся во времени магнитное поле создает электрическое поле; B t - меняющееся во времени создает магнитное поле. 6 D t электрическое поле 6 Ток смещения Максвелл ввел понятие плотности тока смещения, определяемое как: D jсм t - D – электрическая индукция. Ток смещения через поверхность равен потоку вектора jсм через эту поверхность: D I см jсм dS dS t S S 7 7 Ток смещения Магнитное поле создается как токами, текущими в проводниках (токами проводимости), так и переменным электрическим полем (токами смещения). Плотность полного тока: D jполн j jсм j t Обобщение теоремы о циркуляции вектора H: D Hdl I полн ( j t )dS l S Цепь полного тока всегда замкнута. 8 8 Уравнениe Максвелла (1) Обобщение закона электромагнитной индукции: B Edl t dS l S Циркуляция вектора напряженности электрического поля по произвольному замкнутому контуру равна потоку вектора скорости изменения магнитного поля через поверхность, ограниченную данным контуром, взятому со знаком «-». Т.е. переменное магнитное поле вызывает вихревое электрическое поле. 9 9 Уравнение Максвелла (2) Обобщение теоремы о циркуляции вектора H: D Hdl I полн ( j t )dS l S Циркуляция вектора напряженности магнитного поля по произвольному замкнутому контуру равна полному току через поверхность, ограниченную этим контуром. 10 10 Уравнение Максвелла (3) Обобщение теоремы электрической индукции: Гаусса для вектора DdS dV S V Поток вектора электрической индукции через замкнутую поверхность в электромагнитном поле равен свободному заряду в объеме, ограниченном этой поверхностью. 11 11 Уравнение Максвелла (4) Обобщение теоремы Гаусса для вектора магнитной индукции: BdS 0 S Поток вектора магнитной индукции через замкнутую поверхность в электромагнитном поле равен нулю 12 12 B Edl t dS l S D Hdl I полн ( j t )dS l S DdS dV S V BdS 0 S 13 13










