Лекция №7 Компьютерная обработка изображений СПбГУ ИТМО 2003

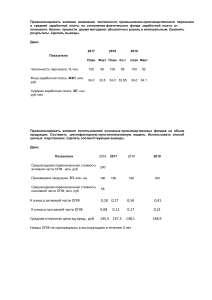
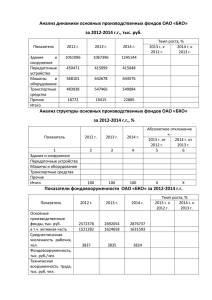
Компьютерная обработка изображений
Лекция №7
СПбГУ ИТМО
2003
Модель формирования изображения
Распределение интенсивности на изображении:


1 



2

I  x ,y  F  F T  x , y
 F  F 1 f  x ,  y
 
 
где
 
  - функция комплексного пропускания предмета;
f  x ,  y  - зрачковая функция;
T  x , y
F
 - оператор преобразования Фурье.
Спектр изображения:


2 
    
 
D x , y  - оптическая передаточная функция (ОПФ).
~
~



I  x , y  I  x , y  D  x , y
~
где I  x , y - спектр предмета;
ОПФ каскада преобразователей
Эквивалентная ОПФ каскада преобразователей:
n
D  D1  D2  ...  Dn   Dk
k 1
где
Dn
- ОПФ отдельного преобразователя.


Смаз: D  x , y  sinc  x a 
Двоение: D  cos  x a 


Вибрация: D  x , y  J 0  x a 
ОПФ некоторых преобразователей
1
0.5
Смаз
Двоение
Вибрация
0
0.5
1
0.25
0.5
0.75
1
1.25
1.5
1.75
2
2.25
2.5
2.75
Обратное преобразование
ОПФ обратного преобразования:

R  x , y

1

D  x , y





~
Тогда: I   x , y 
 
~
I  x , y  D  x , y

D  x , y

  I~
x , y

Можно ли, зная характеристики искажающих
звеньев, улучшить качество изображения?
О возможности восстановления изображения
1.
2.
Если ОПФ имеет точки, в которых D=0,
то восстанавливающий
преобразователь должен иметь ОПФ, в
которой в этих точках R=.
Регистрируется интенсивность
изображения, а не его спектр.
В общем случае восстановление
изображения невозможно!
Обратная фильтрация смаза
Оптическая передаточная функция смаза:

D  x , y

sin  x a 
 sinc  x a  
 x a
Функция обратной фильтрации:
 x a
R x , y  
sin  x a 
Обратная фильтрация смаза
10
10
5
1


R  x , y   x a 
sin  x a 
p( x)
 10
0
0.5
1
1.5
2
2.5
3
5
10
0
x
3
10


5
R1  x , y   x a
0
0.5
1
1.5
2
2.5
3
0
0.5
1
1.5
2
2.5
3
0
0.5
1
1.5
2
2.5
3
5
10

R2  x , y



1


 sign
 sin  x a  
1
1
10


1

R  x , y   x a  sign
 sin  x a  


5
5
10
Обратная фильтрация смаза
Итоговая ОПФ каскада:

D  x , y



sin  x a 
1
  sin  x a 

  x a  sign
 x a
 sin  x a  
1
0
1
0.5
1
1.5
2
2.5
3
Результаты обратной фильтрации
Результаты обратной фильтрации
Спектр изображения при наличии шума
Спектр изображения:

      
 
D x , y  - оптическая передаточная функция (ОПФ);
N  x , y  - спектр шума.
~
~



I  x , y  I  x , y  D  x , y  N  x , y
~
где I  x , y - спектр предмета;
Спектр изображения после применения
обратной фильтрации:


N  x , y
~
~
I   x , y  I  x , y 
D  x , y

 



Фильтрация Винера
Задача минимизации:

2
E  I x   I x    min


Фильтр Винера:
S II  ν 
Dν  
S II ν 
где
S II ( )  F R 
- спектральная плотность;
R    I x I x   dx - автокорреляционная функция;
S II  ( )  F R  - взаимная спектральная плотность;
R    I x I x   dx - функция взаимной корреляции.
Фильтрация Винера

R  x , y

1


D  x , y D  ,
x y

 
ОПФ:
Фильтры Винера:
Инверсные фильтры:

D  x , y

2
 2  S NN  x , y  S II  x , y 
Результаты фильтрации Винера
Результаты фильтрации Винера
Итерационная фильтрация
Итерационный фильтр:

R  x , y


1

  1  D  x , y
D  x , y k  0




k
Пошаговое выполнение фильтрации:
   
~
~
~
I1  x , y   I  x , y   1  D x , y I  x , y  
~
~
 I  x , y   1  D x , y I 0  x , y ;
~
~
I 0  x , y  I   x , y ;
...



 

 

~
~
~
I n  x , y  I   x , y  1  D  x , y I n1  x , y .
Модифицированный итерационный фильтр:



D *  x , y 
k
*






R x , y  


D

,


1

M

,


x
y
x
y
2
M  x , y 
k 0
D x , y 
D *  x , y
Результаты итерационной фильтрации
n=105
n=135