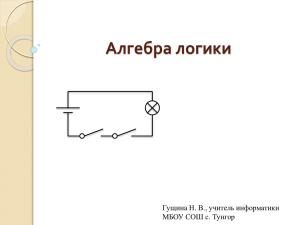
ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ ЛОГИКИ Высказывания и логические операции над ними Основные теоретические положения
реклама

ЭЛЕМЕНТЫ МАТЕМАТИЧЕСКОЙ ЛОГИКИ Высказывания и логические операции над ними Основные теоретические положения Под высказыванием понимают всякое повествовательное предложение, о котором имеет смысл говорить: истинно оно или ложно. Высказывания будем обозначать строчными буквами латинского алфавита: A, B, C, D, .... Истинные высказывания будем обозначать символом И, ложные – символом Л. Отрицанием высказывания A называют высказывание A, истинное, когда B ложно, и ложное, когда A истинно. Конъюнкцией двух высказываний A и B называют высказызание A ^ B, истинное тогда и только тогда, когда истинны оба высказывания A и B. Часто вместо A ^ B записывают AB. Дизъюнкцией двух высказываний A и B называют высказывание A V B, истинное тогда и только тогда, когда истинно хотя бы одно высказывание A или B. Импликацией двух высказываний A и B называют высказывание A → B, ложное тогда и только тогда, когда A истинно, a B ложно. Эквиваленцией двух высказываний A и B называют высказывание A ↔ B, истинное тогда и только тогда, когда оба высказывания истинны или ложны одновременно. Данные определения представим в виде таблицы. A И И Л Л B И Л И Л A Л Л И И A^B И Л Л Л AVB И И И Л A→B И Л И И A↔B И Л Л И С помощью логических операций из элементарных высказываний образуются более сложные – составные высказывания. Конечную последовательность букв, знаков операций и скобок, определяющих структуру высказываний, называют формулой логики высказываний. Две формулы называют равносильными, если при любых наборах переменных высказываний их значения истинности совпадают. Обозначается равносильность символом ≡. Задача 1. Среди нижеследующих предложений выделим высказывания. Определим, какие из них являются истинными, а какие ложными. 1) Спешите делать добро! 2) Закон всемирного тяготения открыл И. Ньютон. 3) В солнечную погоду полезны темные очки. 4) Когда в ы будете в Париже? 5) Число 9 является простым. 6) Сегодня был вкусный обед. Из всех предложений высказываниями являются только: … Высказывания …, ... являются истинными, а высказывания …, .. ложным. Не являются высказываниями: …, … . Задача 2. Сформулируем высказывания, соответствующие формулам: A – Гремит гром. В – Моросит дождь. 1) AB 2) АB 3) А B 4) A↔B Задача 3 Теория Импликация высказываний. Импликацией высказываний A и B называется новое высказывание A → B (читается если A, то B, из A следует B), которое ложно тогда и только тогда, когда истинно, а B ложно. Значение истинности A → B определяется таблицей А И И Л И В A→B И И Л Л И И Л И В импликации A → B высказывание А называется основанием или посылкой, а высказывание В – следствием. Вместо термина импликация встречается термин следование. Задача 3. Докажите равносильность формул: а) (B → С) V (A → С); б) AB → С. Решение. Для доказательства равносильности составим таблицу истинности для данных формул. A 1 И И И И Л Л Л Л B 2 И И Л Л И И Л Л С 3 И Л И Л И Л И Л B→С 4 A→С 5 (B → С) V (A → С) 6 AB 7 AB→ С 8 Истинность формулы а) представить в столбце 6, а истинность формулы б) – в столбце 8. Сравнивая эти столбцы, убеждаемся, что они совпадают, а это значит, что формулы равносильны. Задача 4. Из заданных логических функций эквивалентной A является … 1) A и не А или не А 2) А и не В и А 3) А и не В или А 4) А и не А или В Задача 5. Дан код величины типа Double: 408EF98000000000. Преобразуйте его в десятичное число