Линейное пространство циклов графа над полем Z2=(0,1)
реклама

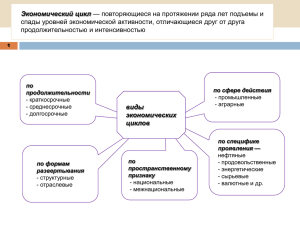
Линейное пространство циклов графа над полем Z2=(0,1) Ерзакова Н.А. профессор кафедры ПМ Определение двоичного кода для цикла графа G с m ребрами. Рассмотрим простые циклы, т.е. циклы, в которых ребра не повторяются. Кодом для цикла Z графа с ребрами e1, e2, …, em называется упорядоченный набор длины m из 0 и 1, (ε1, ε2,..., εm), где εi=1, если ei принадлежит Z и 0, если ei не принадлежит Z. Определение суммы циклов Пусть цикл Z1 имеет код (ε1, ε2,..., εm), цикл Z2 имеет код (α1, α2,..., αm), тогда Z1+Z2 имеет код (α1+ε1, α2+ε2,..., αm+εm). Таким образом, определено пространство циклов. Теорема о размерности пространства циклов Пусть дан произвольный граф G (без петель, без параллельных ребер, с конечным числом вершин) и ν(G)=k. Тогда: из графа G можно удалить k ребер так, что оставшийся граф не имеет циклов, но имеет столько же компонент связности, что и G. размерность пространства циклов графа G равна k. Пример Найти цикломатическое число и базис циклов для данного графа. Решение Решение Решение Решение Находим число вершин |V(G)|=8, число ребер |E(G)|=10, число компонент связности |K(G)|=1, поскольку граф связный. Отсюда цикломатическое число графа ν(G)= |E(G)|-|V(G)|+|K(G)|=10-8+1=3. По теореме о размерности пространства циклов число базисных циклов равно 3. Решение Находим базисные циклы. Для удобства проверки линейной независимости циклов ребра нумеруем в процессе нахождения базисных циклов. Коды циклов: Z1=(1,0,0,0,1,1,1,1,0,0), Z2 =(0,1,0,0,0,0,1,0,0,1), Z3 =(0,0,1,1,0,0,1,0,1,0). Решение Очевидно, ранг матрицы из кодов равен 3. Следовательно, циклы линейно независимые. Число циклов равно цикломатическому числу. Поэтому это базис.