слайды к теме 9
реклама
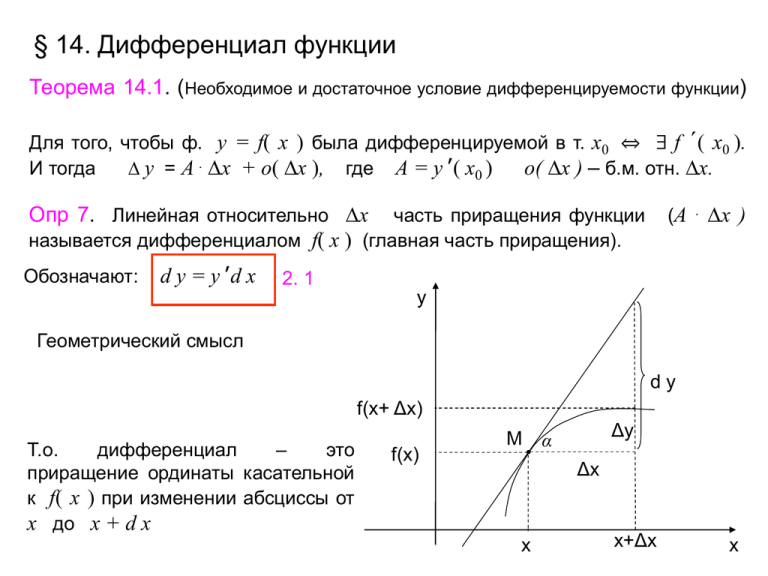
§ 14. Дифференциал функции Теорема 14.1. (Необходимое и достаточное условие дифференцируемости функции) Для того, чтобы ф. y = f( x ) была дифференцируемой в т. x0 ⇔ ∃ f ´( x0 ). И тогда D y = A . Dx + o( Dx ), где А = y' ( x0 ) o( Dx ) – б.м. отн. Dx. Опр 7. Линейная относительно Dx часть приращения функции называется дифференциалом f( x ) (главная часть приращения). Обозначают: d y = y' d x (А . Dx ) 2. 1 y Геометрический смысл dy f(x+ Δx) Т.о. дифференциал – это приращение ординаты касательной к f( x ) при изменении абсциссы от x до x + d x f(x) M Δy α Δx x x+Δx x Свойства дифференциала функции 1. d C=0 2. d ( U + V ) = d U + d V Следствие: если две функции отличаются на постоянную, то их дифференциалы равны d(U+С)=dU 3. d ( U.V ) = V d U + U d V Следствие: постоянный множитель можно выносить за знак дифференциала d ( C.U ) = C d U 4. U V dU U dV d V2 V 5. (свойство инвариантности дифференциала) Дифференциал сложной функции равен произведению производной данной функции по промежуточному аргументу на дифференциал этого промежуточного аргумента. Т.е. если y = f( u ), u = j( x ), то d y = y’x d x = y’u d u Применение дифференциала в приближенный вычислениях Теорема 14.2. Бесконечно малое приращение функции эквивалентно дифференциалу этой функции при всех значениях независимой переменной, для которых производная данной функции конечна и отлична от нуля, т.е. Dy 1 Dx 0 d y lim или D y ~ d y Производные высших порядков Опр 8. Производной n - го порядка для функции y = f ( x ) называется производная от производной (n - 1) - го порядка y ( n ) = ( y (n - 1))' Свойства = u (n) + v (n) 2. ( C.u ) ( n ) = C u ( n ) 3. Пусть u (x) и v (x) имеют производные до n - го порядка включительно. Тогда u (x) . v (x) тоже имеют производную n - го порядка, равную 1. ( u + v ) (n) n (u v) ( n ) Cnk u ( n k ) v ( k ) k 0 u (n) v Cn1u (n1) v Cn2u (n2) v ... Cnn1u v (n1) uv (n) (формула Лейбница) Производные высших порядков от неявных функций Производные высших порядков от параметрически заданных функций Теорема 14.3 Пусть x x(t ) y y (t ) y x( n ) ( y x( n1) )t xt Дифференциалы высших порядков f ( n )( x ).(d x) n переменного d x называется дифференциалом n - го порядка функции f ( x ) в точке x. Опр 8. Степенная функция Обозначают dny d n f ( x) f ( n ) ( x)dx n или d n f (x) отсюда запись: n d f ( x) ( n) f ( x) dx n











