Функция обратной пропорциональности
реклама
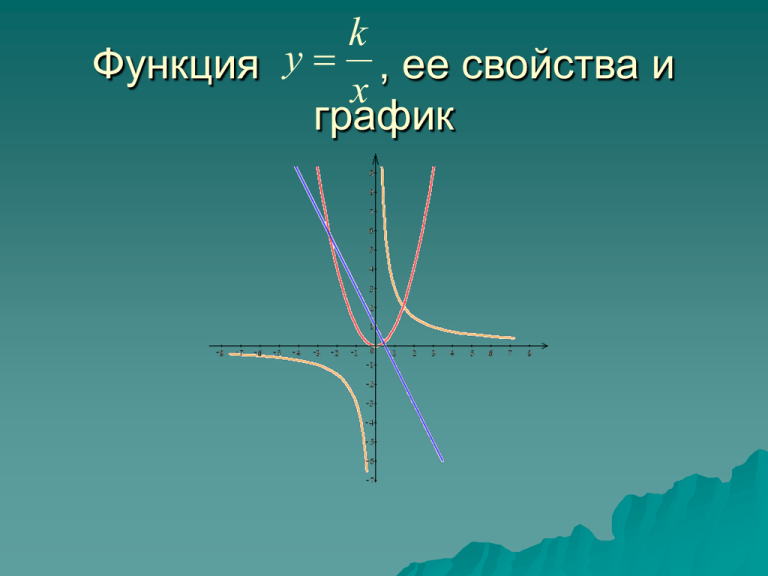
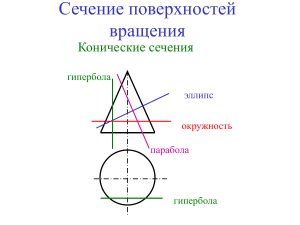
k Функция y , ее свойства и x график Как называются функции, заданные формулами: y = kx y = x³ y = kx+b y=kx² y = (x-a)² +b y= ax²+bx+c Укажите области определения следующих функций: y =x²+8 y 1 x 7 y=(x+9)³ 10 y x y=7 – 5x 2x 7 y x y =(x - 5)² y = 7x 4x 5 y 5 Прочитайте и исследуйте графики функций: 1 2 2 1,5 1 3 2 1,5 1 3 2 1 0,5 0,5 0 -4 -3 -2 -1 0 0 1 2 3 4 -4 -3 -2 -1 -0,5 0 0 1 2 3 4 -2 -1 0 1 2 -0,5 -1 -1 -1 -1,5 -1,5 -2 -2 -3 2,5 6 -2 4 5 1,5 1 6 2 1,5 4 0,5 1 0 -4 -3 -2 -1 2 0,5 0 1 2 3 4 0 0 -0,5 -6 -4 -2 0 2 4 -3 6 -2 -1 -0,5 -1 0 1 2 3 1 2 3 -2 -1 -1,5 -4 -1,5 -2 -2 -2,5 7 8 3 2 2 -2 -1 6 4 2 1 0 -3 9 3 1 -4 -6 -2,5 0 0 0 1 2 3 4 -4 -3 -2 -1 0 1 2 3 4 -3 -2 -1 0 -1 -1 -2 -2 -2 -4 -3 -3 -6 Найдите в таблице графики линейных функций, у которых угловые коэффициенты: а) равны б) равны по модулю и противоположны по знаку 1 2 5 3 4 3 4 2 2 3 0 2 -3 1 -2 -1 0 1 2 1 3 -2 0 -3 -2 -1 0 0 -1 -2 1 2 3 -4 -5 -3 -2 -1 0 -1 -6 -3 -4 -4 -8 -10 -2 -3 1 2 3 4 Известно, что всякая функция описывает процессы, происходящие в окружающем нас мире. х y Рассмотрим прямоугольник со сторонами x и y и площадью 12см². 12 Как изменится y, если х Уменьшить в 2 раза Уменьшить в 4 раза Увеличить в 3 раза Увеличить в 5 раз? Все изменения можно задать формулой 12 y x Мы видим, что если значение х увеличить в 3, 4,5…раз, то значение у во столько же раз уменьшается. Наоборот, если х уменьшать в несколько раз, то у будет увеличиваться во столько же раз. Поэтому функцию такого вида называют обратной пропорциональностью. В общем виде эту функцию можно задать формулой вида у = k/х, где х независимая переменная и k - не равное нулю число. Областью определения такой функции является множество всех чисел, отличных от нуля. На рисунке изображен график функции y = 2/ x. Этот график называют гиперболой. -6 -4 -2 10 10 8 8 6 6 4 4 2 2 0 0 -2 0 2 4 6 -6 -4 -2 -2 0 -4 -4 -6 -6 -8 -8 -10 -10 Если k>0, то график расположен в I и III четвертях, функция является убывающей 2 4 Если k<0, то график расположен во II и IV четвертях, функция является возрастающей 6 Эта кривая была открыта математиками древнегреческой школы в IV в.до н. э. Термин «гипербола» ввел Аполлоний из г. Пергам, живший в III – IIвв. до н. э. что в переводе с греческого означает «прохожу через что – либо». Он показал, что гипербола получается при пересечении кругового конуса плоскостью.