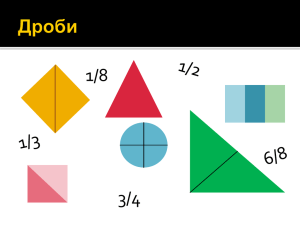
Домашнее задание №8

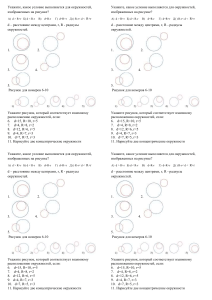
Домашнее задание 4 « Геометрические места точек»
1. Даны две концентрические окружности и точка. Через точку провести окружность,
касающуюся данных окружностей.
Ответ: найти ГМТ центров таких окружностей и ее радиус
2. Через две данные точки провести окружность данного радиуса R.
Ответ: найти ГМТ центров таких окружностей
3. Провести окружность данного радиуса R , касающуюся двух данных окружностей.
Ответ: центр искомой окружности лежит на пересечении двух окружностей с известными
радиусами концентрическими с данными окружностями.
4. На данной прямой найти точку, равноотстоящую от двух данных точек.
Ответ: ГМТ равноотстоящих от данных точек.
5. Провести окружность, касающуюся двух параллельных прямых и третьей прямой,
пересекающей их.
Ответ: пересечение двух известных ГМТ
6. В данную окружность вписать прямоугольник так, чтобы две его смежные стороны
проходили через две заданные точки.
Ответ: ГМТ, из которых данный отрезок виден под данным углом.
7. Построить прямоугольный треугольник по известной гипотенузе и медиане,
проведенной к одному из катетов.
4
Ответ: a 2   c 2  ma2 
3
8. Через точку пересечения двух окружностей провести секущую так, чтобы сумма длин
полученных хорд равнялась a - длине данного отрезка. Какое наибольшее значение
может иметь a ?
Ответ: на отрезке, соединяющем центры окружностей, построить прямоугольный
треугольник с катетом a / 2 .
9. В заданную окружность вписать прямоугольный треугольник с известным острым
углом  , при условии что его катет содержит заданную точку M , расположенную внутри
окружности.
Ответ: отрезок, соединяющий заданную точку M с центром окружности виден из
вершины треугольника под углом  .
10. Около данной окружности описать треугольник с известными углами так, что одна из
его сторон содержит известную точку M .
Ответ: Отрезок OM виден из вершин треугольника под заданными углами.