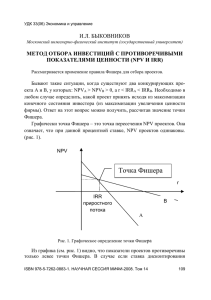
1+i
реклама

Финансовая математика Минасян В.Б. к.ф.-м.н., доцент кафедры корпоративных финансов ВШФМ РАНХиГС при Президенте РФ. Certified International Investment Analyst (CIIA) Типы моделей В зависимости от глубины проникновения в реальные процессы, нужд практики и необходимой точности описания модели финансовой математики подразделяются на: •Статические •Динамические •Детерминированные •Стохастические (случайные) Динамические модели подразделяются на: •Динамические модели с дискретным временем •Динамические модели с непрерывным временем Модели финансовых процессов Под финансовой математикой, в широком смысле, понимаются математические модели для описания процессов, происходящих на финансовых рынках, описания самих рынков и финансовых инструментов, применяемых на этих рынках. Данные модели применяются для оценки важнейших финансово-экономических показателей, описания их взаимной зависимости и динамики во времени. Простые методы Самыми простыми моделями являются статические детерминированные модели. Они присутствуют в финансовом менеджменте, когда мы анализируем ситуацию в данный момент, с помощью данных взятых из прошлого, рассматривая значения некоторых значимых финансовых величин или некоторых их комбинаций, имеющих важный смысл. Например, анализируя (диагностируя) ситуацию в компании с помощью отчетности – применяя соответствующие коэффициенты. Что мы успеем рассмотреть Мы сначала рассмотрим динамические детерминированные модели с дискретным временем. Мы лишь коснемся динамических стохастических моделей с дискретным временем. Простейшая ситуация, требующая введения дискретной модели В дискретных моделях вводят понятие стандартного единого промежутка времени (чаще всего – год). И ситуационно, процесс описывают через каждый стандартный временной промежуток. Простейшая ситуация, требующая введения дискретной модели Предположим, что Вы отдали в долг в момент О сумму Р=PV, и долг должны вернуть через n стандартных временных промежутков. Общеизвестно, что должны вернуть сумму: S = FV = P + I 0 n P S=P+I I – процент,- доход в денежной форме, выплачиваемый кредитору за пользование его деньгами. Схемы начисления процентов Процентная ставка Проценты начисляют по процентной ставке i на стандартном промежутке I i P I – процент за единичный промежуток времени Схемы начисления процентов Схема простых процентов Проценты в размере i начисляются в конце каждого стандартного временного промежутка только на первоначально вложенную сумму Р Схема сложных процентов Проценты в размер i начисляются в конце каждого стандартного временного промежутка, но не только на первоначальную сумму Р, но и на все заработанные к этому моменту проценты. Наращение процентов Наращение простых процентов 0 P n S=P(1+ni) Наращение сложных процентов 0 P n S=P(1+i) n Когда сумма Р вкладывается на банковский депозит, то в договоре между клиентом и банком фиксируется и ставка и схема начисления процентов. Доходность = процентная ставка При вложении суммы Р в финансовые инструменты (активы, бизнесы проекты) более сложные, чем банковский депозит, чаще всего сумма S=FV оказывается случайной. Роль процентной ставки i здесь играет ожидаемая (средняя) доходность от данных вложений за единичное время. Машина времени из настоящего в будущее Будет ли доходность i сложной или простой ставкой зависит от вас. Будете ли вы совершать реинвестирование полученных доходов в конце каждого единичного промежутка времени? n S=P(1+i) при реинвестировании S=P(1+ni) без реинвестирования (1+i) nи (1+ni) соответствующие коэффициенты наращения Концепция временной ценности денег. Дисконтирование. Машина времени из будущего в настоящее Операция оценки современной ценности вложения по известной его будущей ценности называется дисконтированием Дисконтирование по простой ставке. 0 n S P S 1 ni Дисконтирование по сложной ставке. 0 n S P S n (1 i ) Выбор ставки дисконтирования Это нетривиальный вопрос. Иногда, в качестве неё выбирают ставку альтернативной доходности. Но финансовая теория рекомендует выбирать требуемую доходность, зависящую от уровня риска с которым сталкивается инвестор. Этот непростой вопрос решается в недрах корпоративных финансов с помощью различных алгоритмов её оценки в виде WACC – средне-взвешенной доходности, которая зависит от стоимости долга и стоимости собственного капитала инвестора, уровня левериджа с которым он связан и уровнем структурного риска среды, в которой принимается решение. Влияние инфляции на процентную ставку Формула И. Фишера 1 i ip 1 1 h Где i – номинальная (с учетом инфляции) ставка i p- реальная ставка (очищенная от инфляции) h – темп инфляции ip Принцип: Номинальные денежные потоки дисконтировать по номинальным ставкам. Реальные денежные потоки дисконтировать по реальным ставкам Учет векселей по простой и сложной учетной ставках Вексель – это ордерная ценная бумага, подтверждающая безусловное обязательство векселедателя оплатить определенную сумму векселедержателю в определенное время в определенном месте. Учет векселя – это его продажа с передачей права требования новому владельцу (банку) Учет векселей, учетная ставка Банк определяет учетную ставку на стандартном временном промежутке d. И тогда учет векселей может происходить по простой и сложной учетной ставке d. Учет векселей по простой учетной ставке 0 P S (1 nd ) n S- Номинальная ценность векселя Векселедатель передает вексель банку и получает сумму Р Учет векселей по сложной учетной ставке 0 n P S (1 d ) n S Векселедатель передает вексель банку и получает сумму Р Очевидно, что учет векселей связан с дисконтированием. Наращение по учетной ставке Если мы знаем сумму Р, которую получил векселедержатель при учете векселя, и учетную схему, то можно определить номинальную ценность векселя по одной из формул: O n P P P S , 1 nd (1 d ) n В зависимости от того d – простая или сложная учетная ставка Наращение годовой ставки чаще, чем раз в год Эффективная ставка 0 jm m jm m jm m jm m 1 m 2 m 3 m 1 год m Jm – годовая номинальная ставка. Её m-ая доля начисляется в конце каждого интервала деления года на m равных частей с реинвестированием. Эффективная годовая доходность (Эффективная ставка) jm m iэфф (1 ) 1 m Ценность вложения суммы Р через n лет jm mn S P (1 ) m Понятие денежного потока Денежным потоком (постнумерандо/пренумерандо) в течение n стандартных временных промежутков, называется множество денежных платежей или поступлений в конце, или, соответственно, в начале этих промежутков. Мы, в основном, будем рассматривать потоки постнумерандо. CFn 1 0 1 CF1 CF0 CF3 2 CF2 3 n 1 CFn Понятие денежного потока Если это денежный поток от инвестиционного проекта, то рассчитывают чистую приведенную ценность (NPV) проекта CFn CF1 CF2 NPV CF0 ... 1 i 1 i (1 i) n Где i – требуемая ставка доходности Критерий NPV Если NPV>0, то проект, может быть, целесообразно реализовывать. Если NPV 0 , то нецелесообразно финансирование проекта IRR проекта Критерий IRR IRR проекта (внутренней ставкой доходности проекта) называется такая ставка i, при которой NPV(i)=0 Критерий IRR Пусть мы определяем IRR проекта, а i – требуемая ставка доходности. Если IRR>i, то проект целесообразно реализовывать. Если IRR i , то проект нецелесообразно реализовывать Оценка аннуитетов Аннуитетом называется денежный поток, в котором денежные суммы возникают через равные промежутки времени. Мы рассмотрим постоянные аннуитеты, т.е. и сами суммы постоянны и возникают в конце периодов 0 R R R R 1 2 n-1 n Будущая ценность аннуитета S R S n ,i (1 i ) 1 i n S n ,i Современная ценность аннуитета P R An ,i 1 1 n (1 i) An,i i Перпетуитет Вечный постоянный аннуитет (постнумерандо) называется перпетуитетом Современная ценность перпетуитета R P i