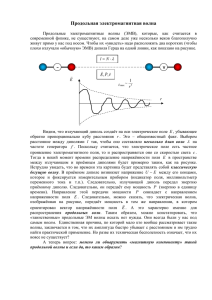
Таким образом, ЭМВ

Лекция 3
Представление гармонических
колебаний
и монохроматических волн в
комплексном виде
можно выбрать и:
Комплексная амплитуда у
скалярной волны означает
наличие начальной фазы и
медленно-меняющейся фазы.
Комплексное число +
комплексно сопряжённое =
удвоенной действительной
части.
Для всех линейных операций
(суммирование,
интегрирование, вычитание,
дифференцирование,
использование граничных
условий и т. д., но не умножение
и возведение в степень) можно
не писать комплексно
сопряженной части
т.е. вместо действительного
выражения использовать
комплексную запись для поля

E( r ,t)
Достоинство комплексного
представления колебательных и
волновых процессов состоит в
простоте обращения с
показательной функцией по
сравнению с
тригонометрическими
функциями.
Если в конечном результате
отделить действительную часть
(удвоив амплитуду) от мнимой,
то получится тот же результат,
что и при использовании
тригонометрических функций.
Векторный характер
электромагнитных волн
( векторные волны )
Поскольку напряженность
электрического поля - величина
векторная, то и ЭМВ - величина
векторная.

Если A - вещественная
величина, то это уравнение
плоской монохроматической
линейно поляризованной волны.

Если A
-комплексная, то
поляризация эллиптическая.
Математическое отступление
Вектор в прямоугольной
системе координат

a 



ax i  a y j  az k
скалярное произведение
векторов




a  ax i  a y j  az k




b  bx i  b y j  bz k

ab  a x bx  a y b y  a z bz
векторное произведение
 
a b 

i

k

j
a a a
b b b
x
y
z
x
y
z
Определитель матрицы

i

k

j
a a a
b b b
x
y
z
x
y
z
x
33



 ( a y b z  a z b y )i  ( a z b x  a x b z ) j  ( a x b y  a y b x ) k
[] [] []
[] [] []
=
+
-
-
+
[] [] []
[] [] []
[] [] []
[] [] []
-
Ротор

i


rot (V ) 
x

j

y

k

z
V V V
x
y
z
Дивергенция
V x V y V z

div (V ) 


x
y
z
Градиент
U x  U y  U z 
grad (U ) 
i 
j
k
x
y
z
Поперечность ЭМВ.
Ортогональность


E и H
Рассмотрим плоские волны в
диэлектрике:





i ( t  k r )
E  E0 e
H  H0 e

i ( t  k r )
Уравнение Максвелла для
плоских волн:

  E

E


E

E
E x 


y
y
z
x
z
rot E  i 



  j

  k
 z
z 
x 
y 
 y
 x

i

  E

j

k
a a a
b b b
x
y
z
x
y
z



 ( a y b z  a z b y )i  ( a z b x  a x b z ) j  ( a x b y  a y b x ) k
Уравнение Максвелла
 E
rot H 
, divH  0
c t
 H
rot E  
, divE  0
c t
Уравнение Максвелла для
плоских волн:



i


rot x E 
x
Ex
j

y
Ey
k

z
Ez
E z E y



y
z
X

 E z ( ik y )  E y ( ik z )  i( E y k z  E z k y )  i [ E k ] x
E z  E0 z e
 i [ t  ( k x x  k y y  k z z )]
.

  E

E


E

E
E x 


y
y
z
x
z
rot E  i 



  j

  k
 z
z 
x 
y 
 y
 x

  E

 Ex  Ey  Ez
div E 


iE k
x
y
z

т.к.
 Ex
 iE x k x
x
и т.д.
Таким образом


rot E  i [ E k ]
и

div E  i E k

а


E
 i E
t
Уравнения Максвелла имеют
вид:


 
i [ H k ]   i E
c

i H k  0



i [ E k ]   i H
c

k
i E k  0


v
c
n
n 
Уравнения Максвелла имеют
вид:


 
i
 [ H n ]  i E
c
c

Hn 0


[ H n ]   E
Уравнения Максвелла имеют
вид:

 

i
 [ E n ]   i H
c
c



 [E n]    H
En 0
Отсюда следует, что

 
E и, Hn
т.е. перпендикулярны
направлению распространения
волны

 
E и, Hn
Таким образом, ЭМВ - волны поперечные.


Итак, E  H
взаимно перпендикулярные
векторы.
  
n ,E ,H
образуют правовинтовую
систему.
  
n ,E ,H
образуют правовинтовую
систему.
, т.е. отношение
E  H
численных значений векторов

E
и

H
от времени не зависит, т.е. эти
векторы обладают одинаковыми
фазами.
В бегущей ЭМВ векторы


E и H
изменяются синхронно.
Энергия, переносимая ЭМВ
Найдем количество энергии,
которое протекает в 1 сек через
площадку в 1 см, которая
перпендикулярна направлению

распространения волны n . Для
этого построим на площадке
параллелепипед (цилиндр), ось

которого параллельна n .
Тогда количество энергии,
которое протекает через
основание параллелепипеда
(цилиндра) в 1 сек, равно
энергии содержащейся в части
параллелепипеда (цилиндра)
длиной 
Следовательно, поток энергии
S  uv ,
где u  плотность энергии
(энергия в единице объёма).
 E2  E
u

4
4
c
v



H
EH
4

c
c  2
S  uv 
EH 
E
4
4


c 
S  uv n 
[E H]
4
(   1)
Вектор Умова-Пойтинга


S
совпадает с n только в
изотропной среде
c
c
2
2
21
S
 E0 cos (   t  kz ) 
 E0 [ 1  cos 2(   t  kz )]
4
4
2
Вектор Умова-Пойтинга

S
изменяется от значения S min  0
до
S max
c
2

 E0
4
Таким образом, поток энергии
колеблется с удвоенной
частотой по сравнению с


E
и
H
около среднего значения
c
2
S 
 E0
8
принимая положительные
значения (включая
S  0 ).
c
2
S 
 E0
8
Поток энергии пропорционален
квадрату амплитуды поля ЭМВ.
Это общее и очень важное
соотношение, на котором
фактически основывается
возможность регистрации ЭМВ
различными приёмниками.
Практически все приёмники света
в той или иной степени
инерционны.
Поэтому они регистрируют
среднее значение квадрата
амплитуды поля
2
E0
(квадратичный детектор).
Световое давление
Поскольку свет электромагнитная
поперечная волна, то падая на
поверхность проводника (зеркально
отражающего или поглощающего
тела), он должен производить
следующие действия:
электрический вектор, лежащий в
плоскости освещенной
поверхности, вызывает ток в
направлении этого вектора


j  E
магнитное поле световой
волны действует на возникший
ток по закону Ампера (сила
Лоренца) так, что направление
действующей силы совпадает с
направлением
распространения света:
 1 
  

Fл  [ j H ]Fл  [ EH ], Fл
c
c


S
Таким образом, взаимодействие
между светом и отражающим
или поглощающим его телом
приводит к возникновению
давления на тело. Сила давления
зависит от интенсивности света.
Для случая, когда световые лучи
образуют параллельный пучок,
давление p по вычислению
Максвелла равняется плотности
световой энергии u (тело
поглощает всю энергию,
абсолютно чёрное тело)
pu
Если часть энергии отражается, то
давление увеличивается в
(1 R) раз, так как при отражении

света, вектор E снова вызывает

ток, а вектор H действует на ток и
появляется сила, направленная в ту
же сторону (так как при отражении
вектора развернулись)
p  u( 1  R )

где R  коэффициент отражения
тела,
для идеального зеркала
R=1  p=2u
Примеры
• 1. Для силы, с которой солнечные лучи в яркий
день давят на чёрной поверхности, Максвелл
вычислил величину
0,4 мГ.
• 2. Опыты П. Н. Лебедева (18991900 гг.). Он с
точностью порядка 20% измерил величину,
рассчитанную Максвеллом. Он использовал
очень чувствительные крутильные весы в
сосуде с откаченным воздухом. Свет
воспринимался тонкими и лёгкими
крылышками.
Примеры
• 3. Оценим давление света от лазерного
импульса длительностью  u и
мощностью Р=1МВт
Примеры
• 4. Левитация это управление движением
малой частицы с помощью лазерного пучка
вопреки силе тяжести.
Расчет сделан для эритроцита.
полностью поглощается
частицей. В принципе можно
организовать не только
удержание, но и движение
частиц
Лазерный пинцет.