Информационное поле и дестабилизация социальных систем С.Ю.Малков, С.Н.Бухарин

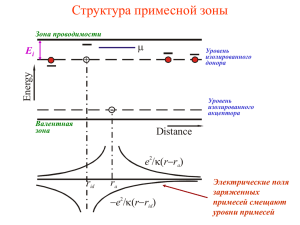
Информационное поле
и дестабилизация социальных систем
С.Ю.Малков, С.Н.Бухарин
Предисловие (1)
Моделирование в социальной сфере нужно для анализа и прогноза
социальных процессов и проектирования социальных систем.
Логично использовать опыт моделирования в естественных науках.
Почему удачен опыт моделирования в физике:
- возможна позиция внешнего наблюдателя (субъект - объект);
- часто можно выделить определяющий фактор (остальные факторы
учитываются как малые добавки);
- часто возможна линеализация модели;
- параметры модели стабильны, существуют законы сохранения;
- возможна проверка (верификация) модели экспериментом,
эксперимент повторяем.
В обществе эти условия не выполняются.
Предисловие (2)
Важная проблема при моделировании социальных процессов: учет
слабоформализуемых факторов. Примеры:
- демография: причины «демографической ямы» в России в 90-х
годах;
- экономика: успешность экономического моделирования в странах
Запада (наличие homo economicus) и неуспешность в странах
Востока;
- политика: слабая предсказательная сила математических моделей.
Попытки учета психологических факторов при моделировании:
- введение в модели поправочных коэффицентов;
- В.А.Лефевр – этические системы;
- теория игр – деонтологические платежные матрицы;
- клеточные автоматы – моделирование коллективного поведения;
- В.Вайдлих – «кооперативное» и «антагонистическое» поведение;
- Д.С.Чернавский – поведенческие функции, условные информации.
Разные основания и предпосылки, фрагментарность рассмотрения.
Предисловие (3)
Чего бы хотелось? – Методического и математического аппарата,
который можно было бы сочетать с отработанными методами
моделирования динамики социальных систем.
X3
dX i
 f i  X i , Y j , ak 
dt
X2
0
X1
Описание динамических систем с помощью дифференциальных
уравнений. Xi – «физические» переменные, Yj – психологические
переменные, ak – параметры.
Предисловие (3)
Чего бы хотелось? – Методического и математического аппарата,
который можно было бы сочетать с отработанными методами
моделирования динамики социальных систем.
X3
dX i
 f i  X i , Y j , ak 
dt
dY j
 g j  X i , Y j , ak 
dt
Y3
X2
Y2
0
X1
0
Y1
Описание динамических систем с помощью дифференциальных
уравнений. Xi – «физические» переменные, Yj – психологические
переменные, ak – параметры.
Попытка формализации:
теория информационного поля (1)
«Информационное поле» задано, если:
А) введена система координат;
Б) задана метрика в фазовом пространстве;
В) определены информационные объекты и законы взаимодействия,
влияющие на динамику их фазовых переменных.
Публикации по тематике «информационного поля»:
Бухарин С.Н., Ковалев В.И., Малков С.Ю. О формализации понятия
информационного поля // Информационные войны, 2009, № 4(12), с.2-9.
Бухарин С.Н., Малков С.Ю. К вопросу о математическом
моделировании информационных взаимодействий // Информационные
войны, 2010, №2(14), с.14-20.
Бухарин С.Н., Малков С.Ю. Информационное поле и проблема выбора
// Информационные войны, 2011, №2(18), с.36-45.
Бухарин С.Н., Малков С.Ю. Эволюция элиты. Материалы и
исследования. - М.: Академический проект; Гаудеамус, 2014.
Попытка формализации:
теория информационного поля (2)
А) Система координат информационного пространства – ценностные
установки субъектов:
ось Y1: положительное направление – «коллективизм», отрицательное
направление – «индивидуализм»;
ось Y2: положительное направление – «примат духовного»,
отрицательное направление – «примат материального»;
ось Y3: положительное направление – «идеал служения», отрицательное
направление – «идеал свободы» и т.п.
Y3
Локализация субъекта Ai в информационном
пространстве – это его «точка зрения»
(самоидентификация).
Б) Метрика.
«Расстояние» в информационном
пространстве между субъектами Ai и Aj:
K
r(Ai, Aj) = rij =
(X
k 1
ik
Аi
rij
Аj
Y2
0
 X jk ) 2
Y1
Попытка формализации:
теория информационного поля (3)
В) Взаимодействие субъектов в информационном поле – гравитационная
аналогия: каждый субъект Ai стремится убедить других субъектов в правоте
своей точки зрения (то есть хочет, чтобы они переместились в точку Ai
информационного пространства).
Сила гравитации: |Fij| = |Fji| = γ∙mi∙mj/rij2 (симметрия).
В информационных взаимодействиях ситуация
сложнее: воздействие и восприятие не равны друг
другу, причем воздействие может быть адресным, а
восприятие – избирательным.
Сила действия Ai на Aj: Fij = k∙qij∙gji∙f(rij),
где Fij – вектор силы, приложенной к объекту Aj и
направленной от Aj к Ai ; коэффициент k отражает
свойства внешней среды; qij характеризует
интенсивность адресного воздействия Ai на Aj; gji
характеризует избирательную восприимчивость Aj к
информационному воздействию со стороны Ai; f(rij) функция информационного расстояния rij между Ai
и Aj (f(r)~1/rs, где s > 1).
Y3
Аi
Аj
Fji
Fij
Y2
0
Y1
Проблема выбора в информационном поле (1)
При принятии решений субъект Ai дает моральную оценку возможным
альтернативам Pn (n=1,..,N). Деонтологическая «полезность» возможных
решений Pn может быть охарактеризована выражением типа:
  R  s

U i ( R)  M i  R  , R  R,
M ,
R  R
 i
где R = R(XРn, Ai) – расстояние в информационном пространстве между точками XРn
и Ai; XРn – локализация решения в ИП; s – параметр, характеризующий степень
уменьшения полезности решения Pn при увеличении значения R (s > 0); Mi –
коэффициент, ΔR – параметр безразличия (он отражает тот факт, что ЛПР при
небольших отклонениях ΔR считает точки Х и Х+ΔR примерно равнозначными).
Чем дальше расположена точка XРn от точки
Ai в информационном пространстве, тем
сильнее моральное неприятие решения Pn
субъектом Ai, тем ниже в его сознании
полезность этого решения, тем с меньшим
желанием он его выберет (даже если оно
будет выгодным по утилитарным
соображениям).
Y3
Аi
R
XPn
Y2
Y1
0
Проблема выбора в информационном поле (2)
Если ЛПР примет решение Рn и последствия этого выбора его удовлетворят
(полученный эффект окажется для него положительным), то произойдет
закрепление осознания полезности такого типа решений и точка
самоидентификации ЛПР Ai сместится в сторону ХPn. Степень смещения зависит от
того, насколько крепок ЛПР в своих убеждениях и не склонен их изменять. Степень
приверженности своим убеждениям зависит от предыдущего опыта ЛПР, от того,
какие «шишки» он набивает на своем жизненном пути. Таким образом, точка
самоидентификации личности Ai не зафиксирована в ИП раз и навсегда. Она
постепенно «дрейфует», отражая накапливаемый жизненный опыт (то есть
Mi(t+1)=Mi(t)+∆m).
Y3
Эволюция субъектов в ИП (сюжеты):
Аi(t)
1) влияние среды;
2) самоидентификакция: индивид –
социальная группа – народ;
Y2
3) влияние возраста на динамику Ai(t);
Y1 0
4) элита – народ, X – Y.
Возможности:
- количественный анализ действия рекламы, СМИ, пропаганды;
- использование в СППР: мониторинг – анализ ситуации – оценка
эффективности мер (бюджетирование) – определение критических состояний.
Политическая стабилизация/дестабилизация (1)
Постановка проблемы:
- различие субъектов в информационном поле есть всегда: rij > 0 (это
следствие различающихся условий жизни);
- как влияет это различие на функционирование социальной системы?
- каковы пороги устойчивости функционирования социальной системы?
Существующие подходы:
dN i
 f i N i , N j , ak  . Проблема: не ясны
• электоральные предпочтения:
dt
пороги устойчивости системы;
• модель борьбы условных информаций (Д.С.Чернавский):
du1
 a1u1  b1u12  c1u1u2 Режим сосуществования и1 и и2 – при b1b2>c1c2.
dt
Невозможность сосуществования и1 и и2 – при b1b2<c1c2.
du 2
 a2u2  b2u 22  c2u1u 2
dt
Проблемы:
а) и1 и и2 всегда конфликтуют. Могут ли они сотрудничать?
б) и1 и и2 антагонистичны (бинарная логика, нет меры близости и1 и и2 .
Ср. ислам в РФ и Афганистане у талибов)
Политическая стабилизация/дестабилизация (2)
Постановка задачи:
при какой структуре и интенсивности взаимных влияний субъектов возникает
согласованность их решений и действий (но не мнений: rij > 0), социальная система
функционирует устойчиво?
Показатели:
индекс рассогласованности мнений Sмij (ИРМ) – всегда больше нуля;
индекс рассогласованности решений Sрij (ИРР) – может быть больше нуля;
индекс рассогласованности действий Sдij (ИРД) – должен быть близок к нулю.
Пример: ИРМ – мнения фракций КПРФ и ЕР,
ИРР – голосование фракций КПРФ и ЕР в Думе,
ИРД – выполнение членами фракций КПРФ и ЕР принятых законов.
0.15
0.15
0.1
0.1
0.05
0.05
0
0
0
20
40
ИРМ
60
80
100
0
20
40
ИРР
60
80
100
Политическая стабилизация/дестабилизация (3)
Аналогия: синхронизация связанных нелинейных динамических систем с
дискретным временем (А.С.Дмитриев).
Пример: синхронизация трех связанных подсистем,
динамика которых описывается дискретным
отображением F(x(t)) с показателем Ляпунова λ >0 (λ ~ rij).
x1(t+1)= F((1-a21-a31)∙x1(t)+ a21∙x2(t)+ a31∙x1(t))
x2(t+1)= F(a12∙x1(t)+ (1-a12-a32)∙x2(t)+ a32∙x1(t))
x3(t+1)= F(a13∙x1(t)+ a23∙x2(t)+ (1-a13-a23)∙x1(t)).
Х1
31
12
13
2
1
Х3
32
23
Х2
Выводы:
- синхронизация может наступить только при превышении интенсивностью связей
определенного порогового значения a' ("порог синхронизации"). При этом, чем более
хаотизированы системы , тем выше значение a' и тем более сильными должны быть связи aij
для того, чтобы предотвратить десинхронизацию систем (aij – это связь между системами);
- в целом при увеличении количества связей порог синхронизации снижается. Однако
возможны ситуации, когда введение новых связей в дополнение к имеющимся не улучшает,
а ухудшает синхронизацию динамики систем. Связи не равнозначны и результат их
взаимодействия существенным образом зависит от общей структуры связей в системе и от
значения λ;
- при опеделенной структуре связей путем увеличения их интенсивности можно
добиться синхронизации при любом значении λ. Однако возможны ситуации, когда при
достаточно больших значениях λ синхронизация не достижима ни при каких
интенсивностях aij .
Системы управления с высокой эффективностью
X1
X1
12
X3
23
13
X2
Вариант 1: жесткая директивная система управления
Особенности: жесткая вертикаль управления,
обратные связи слабые или отсутствуют. Порог
синхронизации высокий.
Примеры: абсолютная монархия, восточная деспотия,
диктатура, тоталитарный режим
Порог синхронизации системы:
'= 12 + 23= 2  (1- exp(-)),
где  - показатель внутренней нестабильности
X3
31
21
12
32
X2
23
Вариант 2: адаптивная система управления
Особенности: задействованы
синхронизации низкий.
все
связи.
Порог
Примеры: демократический режим, парламентская
республика.
Порог синхронизации системы:
' = 12+ 13+ 21+ 23 = 4 ·  = 4 · (1- exp(-))/3,
где  - показатель внутренней нестабильности
X1 – центральная власть, X2 – местные органы управления, X3 – объект управления
Варианты систем управления с пониженной эффективностью
X1
X1
31
12
12
32
X3
X2
23
Вариант 3: директивная система управления с
дополнительной обратной связью 32
\Особенности:
в
дополнение
к
жесткой
управленческой вертикали введена частичная
хозяйственная самостоятельность на местах и
элементы самоуправления. Порог синхронизации
увеличивается
по
сравнению
с
исходной
директивной системой:
 '  12   23  2  1  exp     2  1  exp     23
Для сохранения управляемости необходимо усиление
управляющих воздействий.
X3
X2
23
Вариант 4: директивная система управления с
дополнительной обратной связью 31
Особенности: осуществление непосредственного
влияния народа на центральные органы власти через
выборы, манифестации и т.п. Порог синхронизации
уменьшается, если хаотичность системы низкая, и
увеличивается, если хаотичность системы высокая. В
первом случае управляемость улучшается. Во втором
случае – ухудшается и возможна полная потеря
управляемости вне зависимости от интенсивности
управляющих воздействий 12 и 23
Выводы: - в авторитарных системах необходимо снижать rij (важная роль идеологии, религии):
- переход от авторитарной к адаптивной системе управления (имитационные демократии)
сопровождается остаблением режима;
- это обусловливает эффективность использования «мягкой силы» («цветные революции» и т.п.).
Выводы: - в авторитарных системах необходимо снижать rij (важная роль идеологии,
религии):
- переход от авторитарной к адаптивной системе управления (имитационные
демократии) сопровождается остаблением режима;
- это обусловливает эффективность использования «мягкой силы» («цветные
революции» и т.п.);
- может быть предложен рациональный путь перехода от директивной системы
управления к адаптивной системе управления:
Х1
Х1

Х3

Х2
Х3
Х2
Х1
Х1

Х3

Х2
Х3
Х2
Сюжеты
Пример Квебека
Х2
Х1
Х1 - Квебек; Х2 - федеральные власти Канады
Х3
Х3
Пример Украины

Х2
Х1
Х2
Х1 - Украина; Х2 - Россия; Х3 – США, ЕС
Х1
Публикации по тематике синхронизации/десинхронизации:
Дмитриев А.С., Старков С.О., Широков М.Е. Синхронизация ансамблей
связанных отображений // Известия вузов. Прикладная нелинейная динамика,
1996, т.4, № 4-5, с.40.
Малков С.Ю. Политика с точки зрения синергетики // Стратегическая
стабильность, 1998, №3, с.90-99.
Малков С.Ю. Динамика политических систем: моделирование
устойчивости и дестабилизации // Информационные войны, 2007, №2, с.11-20.
Малков С.Ю. Социальная самоорганизация и исторический процесс:
Возможности математического моделирования. – М.: Книжный дом
«ЛИБРОКОМ», 2009.
Спасибо за внимание
s@malkov.org