ОТЦ Тема 5 Гарм. функции 25.05.2014 18

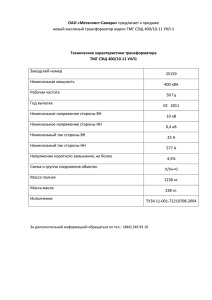
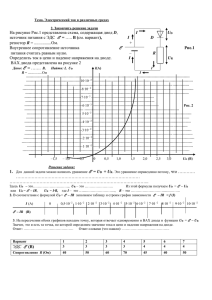
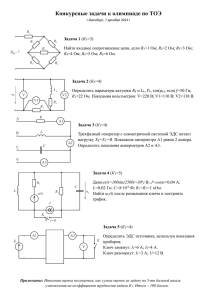
Гарм. величины (ЭДС, напряжение ток). Слайд 1. Всего 18
Тема
ГАРМОНИЧЕСКИЕ ФУНКЦИИ
(ЭДС, НАПРЯЖЕНИЕ, ТОК)
План темы
1. Способы отображения величин, гармонически изменяющихся
во времени.
2. Амплитуда.
3. Период и частота.
4. Способ отображения вращающимся в комплексной плоскости
радиус вектором.
5. Начальная фаза..
6. Сдвиг фаз.
Автор Останин Б.П.
Гарм. величины (ЭДС, напряжение ток). Слайд 2. Всего 18
СПОСОБЫ ОТОБРАЖЕНИЯ ВЕЛИЧИН,
ГАРМОНИЧЕСКИ ИЗМЕНЯЮЩИХСЯ
ВО ВРЕМЕНИ
ИХ ВСЕГО 3
1. Аналитический способ (формулой)
2. Графический способ (графиком во времени)
3. Вращающимся в плоскости радиус вектором
Автор Останин Б.П.
Гарм. величины (ЭДС, напряжение ток). Слайд 3. Всего 18
Аналитический способ
В качестве примера ниже записано
гармонически изменяющееся напряжение u
u  U m sin( t  U )
u – мгновенное (текущее) значение напряжения,
Um – амплитуда напряжения,
 - угловая частота,
t – время,
U – начальная фаза
Начальная фаза может быть отрицательной (u < 0).
Тогда:
u  U m sin( t  U )
Автор Останин Б.П.
Гарм. величины (ЭДС, напряжение ток). Слайд 4. Всего 18
Аналогично можно записать выражения для гармонически
изменяющихся тока i и эдс e
i  I m sin( t  I )
e  Em sin( t  E )
Если начальные фазы отрицательные, то:
i  I m sin( t  I )
e  Em sin( t  E )
Автор Останин Б.П.
Гарм. величины (ЭДС, напряжение ток). Слайд 5. Всего 18
Графический способ
u
+Um
0
t
-Um
T
T – период (время за которое совершается одно полное
колебание периодической величины).
Частота f показывает сколько колебаний совершается за одну
секунду:
f 
Автор Останин Б.П.
1
T
Гарм. величины (ЭДС, напряжение ток). Слайд 6. Всего 18
Графический способ
Обычно на графиках откладывается не время t, а величина t, где
 - угловая частота. Угловая частота , как и частота в герцах f
имеет размерность с-1 (радиан/с () или градус/с (f)). Горизонтальная
координата (t) в этом случае приобретает размерность угла
(измеряется или в радианах, или в градусах). Действительно:
t 
радиан
 с  радиан
с
или
t 
градус
 с  градус.
с
Соотношение угловой частоты и частоты в герцах:
  2 f ,
где f – частота в Гц.
Автор Останин Б.П.
Гарм. величины (ЭДС, напряжение ток). Слайд 7. Всего 18
Ниже показаны графики при t, измеряемой в радианах и в
градусах.
u
+Um
0
-Um
t
-Um
t
T=2
u
+Um
0
T=360
Автор Останин Б.П.
Гарм. величины (ЭДС, напряжение ток). Слайд 8. Всего 18
Далеко не всегда отсчёт t начинается с начала синусоиды.
Угол от начала положительной полуволны синусоиды до нуля
называется начальной фазой и обозначается буквой . Отсчёт
угла до величины  (или до 180) обычно ведут слева направо от
начала ближайшей положительной полуволны (угол 
положительный). При углах больше  (или больше 180) отсчёт
можно вести от начала следующей положительной полуволны
синусоиды. В этом случае угол  будет отрицательным.
u
u
Начальная
фаза нулевая
0
0

Автор Останин Б.П.
u
Начальная фаза
положительная
Начальная фаза
отрицательная
t
0
-
Гарм. величины (ЭДС, напряжение ток). Слайд 9. Всего 18
Способ отображения гармонически изменяющейся
величины вращающимся в комплексной плоскости
радиус вектором
На следующем слайде при последовательном щёлканьи мышкой
будет поворачиваться против часовой стрелки (так принято в теории
цепей) вектор напряжения. Длина вектора меняться не будет.
Справа на графике мгновенных значений будут отображаться точки,
соответствующие текущему положению вектора напряжения. Для
простоты начальная фаза вектора напряжения принята равной нулю
(вектор
расположен
по
положительному
направлению
действительной оси). За один период конец вектора опишет
окружность, а синусоида начертит один период. Следовательно,
один оборот вектора соответствует одному периоду. Например, если
частота напряжения равна 1000 Гц, то вектор должен за одну
секунду совершить 1000 оборотов (и накрутить угол 2000 или
360000), а на графике мгновенных значений должно появиться
1000 синусоид.
Аналогично можно отображать токи и ЭДС.
Автор Останин Б.П.
Гарм. величины (ЭДС, напряжение ток). Слайд 10. Всего 18
Изображение гармонически изменяющегося напряжения
радиус вектором, вращающимся в комплексной плоскости.
Для простоты пусть начальная фаза будет нулевая (u = 0).
Далее щёлкайте мышкой.
u
+j
t2
t1 Um
-1
0
+1
0
t1 t2
t
-j
Автор Останин Б.П.
t
Гарм. величины (ЭДС, напряжение ток). Слайд 11. Всего 18
Чем быстрее вращается вектор (чем больше частота напряжения
), тем больше будет получено синусоид за один и тот же
промежуток времени, например за одну секунду.
Автор Останин Б.П.
Гарм. величины (ЭДС, напряжение ток). Слайд 12. Всего 18
Радиус- вектор. Начальная фаза положительная (u > 0).
Суммарный угол равен t + u
Автор Останин Б.П.
Гарм. величины (ЭДС, напряжение ток). Слайд 13. Всего 18
Радиус- вектор. Начальная фаза отрицательная (u < 0).
Суммарный угол равен t - u
Автор Останин Б.П.
Гарм. величины (ЭДС, напряжение ток). Слайд 14. Всего 18
Сдвиг фаз равен нулю
Автор Останин Б.П.
Гарм. величины (ЭДС, напряжение ток). Слайд 15. Всего 18
Сдвиг фаз равен 30°
Автор Останин Б.П.
Гарм. величины (ЭДС, напряжение ток). Слайд 16. Всего 18
Сдвиг фаз равен 90° (/2)
Автор Останин Б.П.
Гарм. величины (ЭДС, напряжение ток). Слайд 17. Всего 18
Контрольные вопросы 1
1. Перечислите способы отображения гармонически изменяющихся
величин.
2. Поясните аналитический способ отображения гармонически
изменяющихся величин.
3. Поясните графический
изменяющихся величин.
способ
отображения
гармонически
4. Поясните способ отображения гармонически изменяющихся величин
с помощью вращающегося в плоскости радиус-вектора.
5. Укажите размерность произведения ωt.
6. Начертите график гармонической величины с отрицательной
начальной фазой.
7. Начертите график гармонической величины с положительной
начальной фазой.
8. Начертите на комплексной плоскости вектор с положительной
начальной фазой.
Автор Останин Б.П.
Гарм. величины (ЭДС, напряжение ток). Слайд 18. Всего 18
Контрольные вопросы 2
9. Начертите на комплексной плоскости вектор с отрицательной
начальной фазой.
10. Начертите на комплексной плоскости
напряжения с отрицательным сдвигом фаз.
векторы
тока
и
11. Начертите на комплексной плоскости
напряжения с положительным сдвигом фаз.
векторы
тока
и
12. Частота напряжения равна 100 Гц. Укажите угол, который
накрутит вектор, отображающий это напряжение, за одну секунду 1.
в радианах и 2. в градусах.
Автор Останин Б.П.