практика 7 ЭЛЕКТРОМАГНИТНЫЕ КОЛЕБАНИЯ 2015
реклама

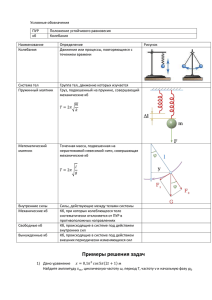
Электромагнитные колебания • • • • Параметры колебательных систем Уравнения колебаний Затухающие колебания Переменный ток Основные формулы T 2 LC Q Qm cos(0t ) dQ I Q 0Qm sin(0t ) I m cos 0t dt 2 Q Qm UC cos(0t ) U m cos(0t ) C C 1 R2 2 LC 4 L Q Qme t cos(t ) Qm Q Qm cos(t ) T Q 1 L R C Um 1 R 2 L C Основные формулы рез 2 1 R 02 22 2 LC 2 L (Qm ) рез Um L 2 02 2 X L L 1 XC C 1 L C tg R 1 X X L X C L C 2 1 2 2 2 Z R L R ( R R ) L C C рез 0 ( I m ) рез Um R 1 LC 1 P I mU m cos 2 cos R 1 2 R L C 2 1. Логарифмический декремент затухания тела, колеблющегося с частотой 50 Гц, равен 0.01. Определить 1) время, за которое амплитуда колебаний уменьшиться в е раз. 2) число полных колебаний тела, чтобы произошло подобное уменьшение амплитуды. Решение: A( t ) sin t A( t ) A0 e t A( t ) A0 e t T A0 t ln A 1 t N e t T 1.1 Начальная амплитуда затухающих колебаний A0. По истечении секунд A0/3. Определить время, по истечении которого амплитуда станет равной A0/10 2. Колебательный контур состоит из катушки индуктивности L, конденсатора C и резистора. Определить сопротивление резистора, если известно, что амплитуда силы тока в контуре уменьшилась в е раз за n полных колебаний. Решение: n T T 1 2L n R 0 1 2 02 2 R 2L LC 1 R2 2 LC 4 L 1 2 2 4L 1 2 RC L R2 C 1 4 2 n 2 3. Колебательный контур состоит из катушки индуктивности L, конденсатора C и резистора R. Определить как измениться добротность контура, если индуктивность увеличить в 2 раза, а емкость уменьшить в 4 раза . Решение: 1 L Q1 R C Q2 1 2L 1 L 8 2 2Q1 R C/4 R C 4. Гармонические колебания напряжения на конденсаторе описываются уравнением U 0.01cos(4 t 8 ) , В. Определите 1) амплитуду колебаний; 2) циклическую частоту; 3) период колебаний; 4) частоту колебаний; 5) начальную фазу колебаний, напряжение через четверть периода. Решение: A 0.01 B U 0.01cos 4 t 8 4 0 8 2 2 1 T сек 4 2 T 1 t сек 4 8 1 5 U 0.01cos 4 0.01cos 8 8 8 5. Колебательный контур состоит из конденсатора емкостью С =100 пФ, катушки индуктивностью L = 0,01 Гн и резистора сопротивлением R = 20 Ом. Определите: добротность контура, период затухающих колебаний; через сколько полных колебаний амплитуда тока в контуре уменьшится в 3e раз. Решение: 1 L Q R C t 1 A0 N ln T A T 2 1 LC 2 R2 2 4L t T A0 1 N ln T A R 2L 2 L A0 2 L N ln ln 3 RT A RT 1 ln A0 A 6. Запишите уравнение затухающих колебаний, если максимальная величина заряда q0 составляет 10 нКл, период затухающих колебаний T = 3 с, логарифмический декремент затухания θ=0,03, начальная фаза колебаний равна 30 градусов. Решение: 0.03 0.01 с 1 T 3 2 2 T 3 q q0e t cos t 0 q 10 e 0.01t 2 cos t 6 3 6.1 Запишите уравнение затухающих колебаний, если максимальная величина заряда q0 составляет 100 нКл, период затухающих колебаний T = 5 с, время релаксации 0,03 сек, начальная фаза колебаний равна 60 градусов. 7. По графику зависимости напряжения от времени на резисторе сопротивлением 100 Ом найти максимальное значение напряжения и силы тока на резисторе, среднюю мощность, выделяемую током на резисторе. Написать уравнения зависимости напряжения и силы тока от времени на резисторе. Решение: U m 50 В T 0.8 c Um Im 0.5 A R P I дU д I mU m U m2 P 12.5 Вт 2 2R 2 2 2.5 с 1 T 0.8 u U m cos t 50cos 2.5 t i I m cos t 0.5cos 2.5 t 8. В цепи, показанной на рисунке, конденсатор емкостью С1 = 10−5 Ф вначале заряжен до напряжения U1 = 200 В, а конденсатор емкостью С2 = 10−6 Ф разряжен. До какого максимального напряжения U2max может зарядиться конденсатор С2 в процессе колебаний, возникающих в цепи после замыкания ключа? Потерями в соединительных проводах и в катушке индуктивности пренебречь. Решение: C1U1 q C1U q2 2 2C1 2C2 2 2 1 2U1C1C2 q C1 C2 U 2 max q U2 C2 2U1C1 364 В C1 C2 9. В цепи переменного тока с частотой 50 Гц и действующим напряжением 300 В последовательно включены конденсатор, резистор 50 Ом и катушка 0.1 Гн. Падения напряжения U1/U2 как ½. Определить электроемкость и действующее значение силы тока Im Решение: Im U m1 R2 1 C 1 R 2 L 2 2 1 2 3R 2 42L 2 Im R 2 L 1 C U m2 Im C Um 30 мкФ Um R 2 L 1 C 2 3.3 мА 2 10. Найти формулы для полного сопротивления цепи Z и сдвига фаз между напряжением и током φ при различных включениях сопротивления R, емкости C и индуктивности L : 1) R и С включены последовательно, 2) R и С включены параллельно, 3) L и С включены последовательно, 4) L и С включены параллельно, 5) R , L и С включены последовательно Решение: Z R L 1 C 2 Im Um 2 Im UC cos t С 2 U L I mL cos t 2 2 U R I m R cost R L 1 C 2 1 L C tg R U R U C U L U m cos t 10.1) R и С включены последовательно L=0 Im Um R 1 C 2 2 1 tg CR 10.2) R и С включены параллельно – две параллельных цепи в которых только R и C соответственно 1 1 2 C 2 Z R IС U mС IR Um Z R 1 R 2 2C 2 IС tg RC IR R 10.3) R и L включены последовательно C=0 Im L tg R Um R L 2 2 10.4) R и L включены параллельно – две параллельных цепи в которых только R и L соответственно 1 Z IR Um R IL Um L 1 1 2 R L 2 Z R L R 2 2 L2 IL R tg IR L 10.5) R , L и С включены последовательно Im Um 1 R L C 2 tg L R 1 C 2 11. Для схемы определить ток в цепи, коэффициент мощности, активную и реактивную и полную мощность и построить векторную диаграмму Решение: 1. импеданс 2. Полный ток в цепи U I 5А Z 4. Полная мощность Z r1 r2 r3 X L X C 2 2 20Ом 3. Коэффициент мощности цепи r1 r2 r3 cos 0.8 Z 5. Активная мощность 37 6. Реактивная мощность S UI 500ВА P S cos 400 Вт Q S sin 300 Вар S I Z 500 ВА 2 P I 2 r1 r2 r3 400Вт X L XC sin 0.6 Z 12. В колебательном контуре, содержащем катушку индуктивности L и конденсатор C и резистор R, поддерживаются незатухающие гармонические колебания. Определить амплитудное значение напряжения на конденсаторе UmC, если средняя мощность, потребляемая колебательным контуром, составляет Pср. Решение: Pср 2 m I R Pср 2 I m CU mC 0 1 LC 2 CU mC 2 R C 2U mC 2R 2 2 2 CU mC R Pср 2L U mC 2 LPср RC 3.1 Колебательный контур состоит из конденсатора емкостью С, катушки индуктивности L и сопротивления R. Какую среднюю мощность должен потреблять контур, чтобы в нем поддерживались незатухающие колебания с амплитудным значением напряжения на конденсаторе U0 13. Определить характер нагрузки, полную, активную и реактивную мощности цепи, в которой мгновенные значения напряжения и тока составляют U=282sin(ωt+60°); I=141sin(ωt+30°) Решение: 1 60о 2 30о 1 2 30о - активно-индуктивный характер S IU Im Um 2 141 282 20 103 В А 2 2 2 P S cos 17,3 103 Вт Q S sin 103 вар 14. Колебательный контур состоит из конденсатора емкостью С, катушки индуктивности L и сопротивления R. Какую среднюю мощность должен потреблять контур, чтобы в нем поддерживались незатухающие колебания с амплитудным значением напряжения на конденсаторе U0 Решение: 0 1 LC Q Q N t T U U 0 sin 0t t T dq dU C Q I Rdt I dt dt t 2 I СU 00 cos0t t T 2 2 2 RС U 0 0 T 2 2 2 2 Q RС U 0 0 cos 0t dt 2 t RС 2U 0202 N 2 08.В 1колебательном последовательном контуре происходят вынужденные LC U гармонические колебания. При частотах вынуждающей ЭДС I =C 300 с-1 и 01 0 2 = 600 амплитуда силы тока составляет половину своего максимального значения. Определить частоту собственных колебаний и резонансную частоту вынуждающей ЭДС. с-1 Решение: U0 002 2 0 4 2 р 2 2 0 0 2 I0 2 0 L 02 12 4 212 0 4L L 02 2 4 2 2 0 I 0 ,max 2L 2 00 0 L 02 22 4 222 0 4L 0 0 2 2 2 2 L 0 2 4 2 4 L 0 0 2 2 2 2 L 4 4L 0 1 1 L L 0 2 2 4 2 2 2 0 0 1 1 2 0 2 4 2 0 4L 0 4L 2 2 0 2 4 2 16 2 2 2 2 0 2 2 4 16 1 1 02 12 2 2 2 0 12 1 1 2 1 2 1 2 0 2 0 0 1 2 0 424с 1 02 1 12 1 2 1 12 р 02 2 2 р 406с 1 2 0 1.3 Существенное отличие резонансной частоты от собственной частоты свидетельствует о быстром затухании колебаний – большом логарифмическом декременте затухания ВОПРОСЫ К КОЛЛОКВИУМУ № 2 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. Две формы уравнения колебаний, примеры колебательных систем Параметры колебательных систем. Энергия при колебательном движении. Затухающие колебания Вынужденные колебания Резонанс, автоколебания и другие виды колебательных движений Метод векторных диаграмм. Пример. Сложение колебаний одинакового направления Сложение взаимно-перпендикулярных колебаний Примеры колебательных систем. Параметры систем. Физический маятник. Приведенная длина. Гармонические электромагнитные колебания Затухающие электромагнитные колебания. Вынужденные электромагнитные колебания. Резонанс в различных контурах. Метод диаграмм. Переменный ток. Закон Ома. Импеданс. Переменный ток . Мощность.