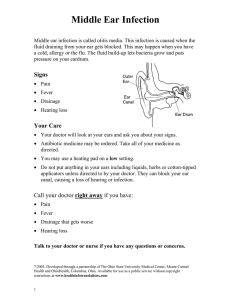
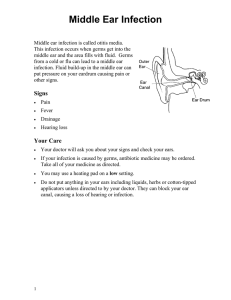
Фундаментальные физиологические механизмы в моделях

Basic physiological mechanisms and
mathematical models of infection diseases
Romanyukha A A
INM RAN Moscow
Main items
• Indexes of disease’s dangerous and maintenance
of internal environment homeostasis
• Models of infection diseases and physiological
adaptation
Laboratory index (viral hepatitis)
•
•
•
•
b – bilirubin 1 concentration (sign of liver damage )
B – bilirubin 2 concentration (sign of liver damage )
- reduced bilirubin
f – the enzyme concentration in blood (sign of liver cell
destruction)
• β – concentration in blood the species produced in liver
under stress (sign of liver disfunction)
b  K1 ( p)[1 ( p  p0 )   2 ( f  f 0 )   3 (   0 )] 
4 b  B
 K 2 ( p)[ 
]

f
Laboratory index dynamics during viral hepatitis
natural course
b
3
2
1
5
10
15
20
t (days)
Normalized laboratory index dynamics
during viral hepatitis course
b
1
5
10
15
20
t (days)
Dotted lines stand out trajectories with high rate of favorable
disease outcome
Index of Inflammation (viral infection)
The aim – estimation of defense reaction magnitude and
its concordance with clinical state (index)
• T – body temperature; H – heart rate; AD – arterial
pressure T0 , H0, AD0 – normal values
IV = 0.1(T-T0)+0.05(H-H0)+0.6(AD-AD0)
• But the index says nothing about mechanism(s)
determined unfavorable disease outcomes.
From indexes of disease dangerous
to models of infection diseases
• The design of all indexes based on estimation
of deviation from normal state of homeostasis.
• But the index says nothing about mechanism(s)
determined unfavorable disease outcomes.
Basic model of infection disease. Marchuk , 1973
The state of health


C
if V  0 (means health), then C  C , F 
, m  0.
F


• To ill or not to ill depends from inequality:
• State of health is unstable
• State of health is stable
if    F * then VTo  0.
if    F * then VTo  0
• That mechanism determined value of C*?
Energy cost of immune defense
• Е0 – energy cost of immune defense include two
components:
Е1 – energy cost of immune system maintenance
during health and
Е2 – energy cost of infection disease itself, then
Е0=Е1+Е2
Estimation of energy cost of immune defense
• Е1 energy cost of health: cost of immune cells maintenance and
renewing – approx – 2 – 2.5 W (permanent, running cost)
•
Energy cost of diseases : cost of inflammation, immune
response, regeneration…. (25 – 150 W during several days of
acute disease) multiply on number of diseases.
• Assume that in normal organism E1  E2
• Why?
Relations between E1 and E2
Immune system adaptation to increase of antigenic
load
Е2
1
2
B
C
M2
M1
D
Е1
Energy cost of immune defense change with aging
Е2
Death
Senior
weak IS
Child
Adult
normal IS
Reproductive period
Non-reproductive period
strong IS
Е1
Characteristic property of model
• The design of model permit estimate of defense
effectivity (target organ damage, inflammation,
homeostasis disturbance….)
• This allow to describe immune system adaptation
and possible cause of immune suppression.
Публикации
1.
Romanyukha, A.A., S.G. Rudnev, I.A. Sidorov. 2006. Energy cost of
infection burden: An approach to understanding the dynamics of host–
pathogen interactions. J Theor. Biology v 241, pp. 1-13
2.
3.
4.
Романюха, А.А., Руднев. С.Г. 2001 О применении одного вариационного
принципа в задачах исследования противоинфекционного иммунитета
на примере математической модели пневмонии. Математическое
моделирование, т.13, №8, с.65-84
Marchuk, G. I., & Romanyukha, A. A. (2010). Mathematical modelling and
the homeostatic function of the immune system. Russian Journal of Numerical
Analysis and Mathematical Modelling, 25(6), 563-580.
Романюха АА Иммунная система, норма и адаптация. Иммунология.
2009 №1 стр.7-13