panfilova gazovie zakoni

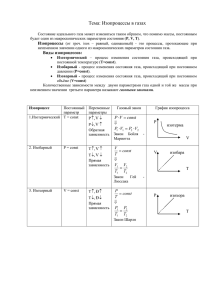
Всероссийский интернет – конкурс педагогического творчества
(2015-2016 учебный год)
Номинация конкурса: педагогические идеи и технологии среднее образование
Название работы: Урок физики «Изопроцессы. Газовые законы. Решение задач» (10
класс)
Автор: Панфилова Татьяна Львовна, учитель физики средней школы №88
г.Ярославля
План-конспект урока по физике «Изопроцессы. Газовые законы.
Решение задач» (10 класс)
Цели:


Сформировать понятие об изотермическом, изобарном и изохорном процессах.
Познакомить учащихся с практическим применением газовых законов
Продолжить развитие умений
 работать с различными источниками информации,
 анализировать явления,
 использовать приобретенные знания в жизни.
Ход урока
I.
II.
Организационный момент (2 мин)
Актуализация опорных знаний(5 мин)
Класс - фронтально повторение изученного ранее, 2 чел к доске- разбор
домашних задач №495 и 500 (Рымкевич)
- Что такое идеальный газ?
Это газ, взаимодействие между молекулами которого пренебрежимо мало
- Что такое макроскопические параметры?
Величины, характеризующие состояние макроскопических тел без учета их
молекулярного строения (p,V,t), называют макроскопическими
параметрами.
- Запишите уравнение, связывающее макроскопические параметры
𝑝𝑉 =
𝑚
𝑇
ℳ
- Как называется данное уравнение?
Уравнение состояния или уравнение Менделеева-Клапейрона
- Как выглядит данное уравнение в форме, предложенной Клапейроном?
𝑝𝑉
= 𝑐𝑜𝑛𝑠𝑡
𝑇
- На какие вопросы можно дать ответ , используя уравнение состояния?
1. Уравнение позволяет определить одну из макроскопических величин, если
известны две другие.
2. Используя уравнение состояния, можно сказать, как протекают в
системе различные процессы при определенных внешних условиях.
3. Используя уравнение состояния, можно определить, как меняется
состояние системы, если она совершает работу или получает теплоту от
окружающих тел.
Разбор домашних задач №495 и 500 (Рымкевич) – комментарии учащихся,
работающих у доски
III.
Изучение нового материала(15 мин)
Рассмотрим процессы, протекающие с неизменной массой газа и неизменным
одним из макроскопических параметров.
Количественные зависимости между двумя параметрами газа при фиксированном
значении третьего называют газовыми законами (запись в тетеради).
Процессы, протекающие при неизменном значении одного из параметров без
изменения массы газа, называют изопроцессам (запись в тетради).
Изопроцесс - идеализированная модель реального процесса, которая только
приближенно отражает действительность. Только в лабораторных условиях можно
поддерживать постоянство того или иного макроскопического параметра с высокой
точностью, в действующих технических устройствах и природе это практически
невозможно.
Параметры
сравнения
Изотермический
процесс
Определение
Изопроцесс,
Изопроцесс,
протекающий
при протекающий при
постоянной
постоянном давлении,
температуре,
называется
называется
изотермическим
изотермическим
процессом
процессом
m=const, T=const
m=const, p=const
Постоянные
величины
Вывод
газового
закона
𝑝𝑉
= 𝑐𝑜𝑛𝑠𝑡
𝑇
Изобарный
процесс
𝑝𝑉
= 𝑐𝑜𝑛𝑠𝑡
𝑇
Газ из состояния с Газ из состояния с
параметрами
параметрами (p,V1,T1)
(p1,V1,T) переходит в переходит в состояние
состояние
с с
параметрами
параметрами
(p,V2,T2), тогда
(p2,V2,T), тогда
p ∗ V1 p ∗ V2
=
p1 ∗ V1 p2 ∗ V2
𝑇1
𝑇2
=
𝑇
𝑇
Изохорный
процесс
Изопроцесс,
протекающий при
постоянном объеме,
называется
изотермическим
процессом
m=const, V=const
𝑝𝑉
= 𝑐𝑜𝑛𝑠𝑡
𝑇
Газ из состояния с
параметрами (p1,V,T1)
переходит в состояние
с
параметрами
(p2,V,T2), тогда
p1 ∗ V p2 ∗ V
=
𝑇1
𝑇2
следовательно,
p1*V1=p2*V2
Формулировка
закона
Графическое
изображение
процесса
следовательно,
следовательно,
p ∗ V1 p ∗ V2
p1 ∗ V p2 ∗ V
=
=
𝑇1
𝑇2
𝑇1
𝑇2
pV=const
–закон 𝑉 = 𝑐𝑜𝑛𝑠𝑡- закон Гей- 𝑝 = 𝑐𝑜𝑛𝑠𝑡- закон Шарля
𝑇
𝑇
Бойля –Мариотта.
Люссака
Для данной массы газа
Для данной массы
Для данной массы при постоянном объеме
газа при постоянной
давления
газа при постоянном отношение
температуре
газа
к
его
температуре
давлении отношение
произведение
объема газа к его постоянно.
давления газа на его
температуре
объем постоянно.
Закон
постоянно.
экспериментально
Закон
открыт в 1787 году
Закон
экспериментально
Ж.Шарлем
экспериментально
открыт Р.Бойлем и
открыт в 1802 году
несколько
позже
Ж.Гей-Люссаком
Э.Мариоттом
Зависимость
Зависимость объема Зависимость давления
давления газа от газа от температуры газа от температуры
объема
при при
постоянной при
постоянной
постоянной
температуре
температуре
температуре
графически
графически
графически
изображают кривой, изображают
кривой,
изображают кривой, которую
называют которую
называют
которую называют изобарой
изохорой
изотермой.
V1 𝑇1
p1 𝑇1
=
=
p1 V2
𝑉2 𝑇2
𝑝2 𝑇2
=
𝑝2 𝑉1
Для того,
обеспечить
постоянство
чтобы Изобарным
можно Изохорный
процесс
считать расширение используется в газовых
(сжатие) газа при его термометрах
температуры,
нагревании
постоянного объема
необходимо, чтобы (охлаждении)
в
сжатие
или цилиндре
с
расширение
подвижным поршнем,
происходило очень если
внешнее
медленно
давление постоянно
IV.
Первичное закрепление(15 мин)
Решение расчетных задач - можно параллельно решать на доске для экономии
времени с последующей проверкой( одна задача вслух, вторая-четвертая самостоятельно)
№516 (изотермический процесс),
№527 (изобарный процесс)
№539 (изохорный процесс)
№520
V.Решение графических задач
Изучение нового материала (8+5 мин)
Задача 1.
Изобразить данный процесс в координатах (pT) и (VT)
p
4
1
3
2
V
Алгоритм решения:
1. В каждом процессе определить, есть ли неизменный мкроскопический
параметр и как изменяются два другие (если необходимо, применить
газовые законы)
2. В данных осях изобразить точку 1 и начать построение процессов,
используя шифровку.
1-2:изохорный, V=const, p↓, по закону Шарля T ↓
2-3: изобарный, p=const, V↓, по закону Гей Люссака T↓
3-4: изохорный, V=const, p↑, по закону Шарля T ↑
2-3: изобарный, p=const, V↑, по закону Гей Люссака T ↑
p
1
4
V
3
1
2
3
2
4
T
T
Задача 2. №543 (Рымкевич)
V
2
1
V1
V2
T
T0
Алгоритм решения:
1. Через точки 1 и 2 проводим изо- (термы, бары, хоры – в зависимости от
координатных осей)
2. Фиксирует один из параметров
3. На второй оси отмечаем точки, получившиеся при пересечении
построений из п.1 и п.2
4. Применяем уравнение состояния и делаем вывод об изменении искомого
параметра
Через т.1. и т.2 проведем изобары
Зафиксируем температуру, проведя перпендикуляр к соответствующей оси
Перенесем на ось V получившиеся значения V1 и V2, сравним их.
Применим уравнение состояния для полученных точек
p1 ∗ V1 p2 ∗ V2
=
𝑇0
𝑇0
p1 V2
=
𝑝2 𝑉1
V1 > V2, следовательно p1 < p2, т.е. давление увеличивается.
VI.
Закрепление (20мин)
Решение задачи №542, 544,545(А.П.Рымкевич. Задачник для 10-11 классов)
у доски
VII.
Самостоятельная работа (15 мин)
1 вариант
1. Изобразить процесс в осях (pV) и
(pT)
V
2 вариант
1. Изобразить процесс в осях (pV) и
(VT)
p
2
1
2
1
3
3
T
2.Упражнение 13 (6)
VIII. Итог урока, рефлексия (5 мин)
T
IX.
Домашнее задание – №517, 529, 538, индивидуальные графические задачи
Информационные источники
1) А.П.Рымкевич Физика. Задачник. 10-11 класс. Пособие для общеобразовательных
заведений – М., Дрофа, 2010
2) Г.Я.Мякишев, Б.Б.Буховцев, Н.Н.Сотский; под ред. В.И.Николаева Физика 10
класс: учебник для общеобразовательных учреждений (базовый и профильный
уровни) М., Просвещение, 2010 г.