6565
реклама

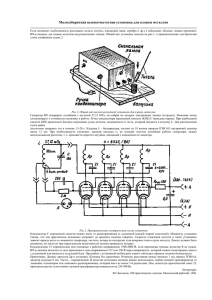
6565. На цилиндрическую часть катушки радиусом r = 10 см, лежащей на столе, намотана легкая нерастяжимая нить, отрезок АВ которой горизонтален (см. рисунок). В момент времени t = 0 точку нити A начинают тянуть с постоянным горизонтальным ускорением a, модуль которого равен 4 см/с2. При этом катушка начинает двигаться без проскальзывания так, что ее ось не изменяет своей ориентации. Через какое время τ длина горизонтального участка нити изменится в n=2 раза, если длина отрезка АВ была равна L0 = 1 м, а внешний радиус катушки равен R = 20 см? Дано: L0=1 м; n=2; R=0,20 м;r =0,10 м; a=4 м/с2. Найти: τ=? Решение. По условию задачи при перемещении точки нити A катушка движется по плоскости, сохраняя ориентацию своей оси. Следовательно, считая катушку твердым телом, ее движение можно представить как сумму поступательного движения со скоростью v0, равной скорости движения оси катушки, и вращения с угловой скоростью ω вокруг этой оси. Поскольку качение катушки происходит без проскальзывания, то 𝑣0 𝝎= . 𝑅 Из сказанного следует, что в тот момент, когда скорость оси катушки равна ω, скорость точки B должна быть равна (𝑅 − 𝑟) ∙ 𝑣0 𝑣𝐵 = 𝑣0 − 𝜔 ∙ 𝑟 = , 𝑅 а потому при движении катушки с течением времени длина отрезка нерастяжимой нити AB должна уменьшаться. Учитывая, что по условию задачи отрезок нити АВ остается горизонтальным, а первоначально покоившуюся точку A перемещают с постоянным ускорением a, коллинеарным нити, искомый промежуток временит должен удовлетворять уравнению (𝑎0 − 𝑎) ∙ 𝜏 2 𝐿0 𝐿(𝜏) = = 𝐿0 − , 𝑛 2 где 𝑎∙𝑅 𝑎0 = 𝑅−𝑟 - ускорение центра катушки. Из этих уравнений следует, что 𝑎 ∙ 𝑛 ∙ 𝑟 ∙ 𝜏 2 = 2 ∙ 𝐿0 ∙ (𝑛 − 1) ∙ (𝑅 − 𝑟), и с учетом условия 0≤𝜏 интересующий промежуток времени равен 2 ∙ 𝐿0 ∙ (𝑛 − 1) ∙ (𝑅 − 𝑟) 𝜏=√ . 𝑎∙𝑛∙𝑟 Вычисления в СИ: 2 ∙ 1 ∙ (2 − 1) ∙ (0,2 − 0,1) 𝜏=√ 𝑐 = 0,5 𝑐. 4 ∙ 2 ∙ 0,1 Ответ. 𝝉=√ 𝟐 ∙ 𝑳𝟎 ∙ (𝒏 − 𝟏) ∙ (𝑹 − 𝒓) , 𝝉 = 𝟎, 𝟓 𝒄. 𝒂∙𝒏∙𝒓