Институт страхового и инвестиционного бизнеса ФИО: Вебинар

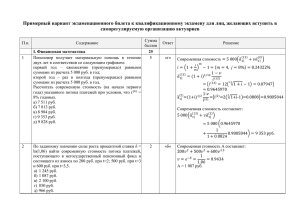
Институт страхового
и инвестиционного бизнеса
ФИО:
Вебинар
17 сентября 2015 г.
Условие задачи
Ваш
ответ
Начисляем
балл
1. Вычислить
, используя
иллюстративные основную и селективную таблицы
смертности и предполагая равномерное распределение
смертей внутри года.
а) 10,2
б) 13,4
в) 17,7
г) 25,3
д) 32,4
6 баллов
2. Рассматривается договор смешанного страхования жизни
на срок 10 лет с выплатой страховой суммы в конце года
смерти или по окончанию срока страхования. Вы
располагаете следующей информацией:
Определите
.
а)
Менее 70
б)
Не менее 70, но менее 72
в)
Не менее 72, но менее 74
г)
Не менее 74, но менее 76
д)
Не менее 76
5 баллов
3. Компания по страхованию жизни заключила договор
пожизненного страхования с застрахованным лицом в
возрасте x = 47 лет. Договором предусмотрена выплата
страховой суммы S = 10 000 рублей в конце года смерти.
Брутто-премия P = 265 рублей уплачивается ежегодно в
начале очередного года страхования. При расчете бруттопремии были сделаны следующие предположения:
Таблица смертности: Актуарная иллюстративная таблица
смертности (основная).
1
Процентная ставка: i = 5% годовых.
Комиссия второго и последующих лет: c% от годовой премии.
Расходы второго и последующих лет: D = 75 рублей за год в
начале второго и последующих годов страхования.
Расходы при выплате страхового обеспечения: e = 1% от
страховой суммы.
Брутто-резерв по полису на конец 14-го года страхования
равен 651,83 рублей.
Определите, какую комиссию (в % от годовой премии)
уплачивает компания агенту, если известно, что брутторезерв по договору на конец 15-го года страхования составил
774,67 рублей.
а)
2,50%
б)
3,00%
в)
3,50%
г)
4,00%
д)
4,50%
5 баллов
4. Для пожизненного страхования лица в возрасте 50 лет,
оплачиваемого ежегодными премиями G, вносимыми в
начале очередного года страхования в течение всего срока
договора, дано:
1) Выплата на случай смерти составляет 3000 рублей в
течение первых 8 лет страхования и 6000 рублей в
последующие годы и производится в конце соответствующего
года страхования.
2) Расходы, выплачиваемые в начале года, равны 200 рублей
в первый год страхования и 20 рублей, начиная со второго
года.
3) π – размер ежегодной брутто-премии, определяемый с
использованием принципа эквивалентности.
4)
– размер ежегодной брутто-премии, указанной
в договоре.
5) Смертность определяется на основе Актуарной
иллюстративной таблицы смертности (основной).
6) Процентная ставка: 6% годовых.
7)
Рассчитайте брутто-резерв по договору на конец первого года
его действия, исходя из премии, указанной в договоре.
а) -138,53
б) -143,29
в) -149,66
г) -154,75
д) -160,02
5 баллов
5. Кумулятивный треугольник развития убытков имеет вид:
2
Число поданных исков:
Вычислите резерв неоплаченных убытков методом средней
стоимости.
а) 13630
б) 13850
в) 13960
г) 14110
д) 14350
6 баллов
6. У страховой компании есть два портфеля независимых
полисов, в которых страховые случае происходят в
соответствии с законом распределения Пуассона. В первом
портфеле все страховые случаи имеют фиксированный
размер 5 000 руб. и ожидаемое число убытков за год
составляет 10 случаев. Для второго портфеля убытки
распределены по экспоненциальному закону, средняя
выплата составляет 4 000 руб. и ожидается 30 страховых
случаев за год. Обозначим через S совокупный убыток по
двум портфелям. Страховщик включает в премии нагрузку
10% для всех полисов.
Используя аппроксимацию распределения S нормальным
распределением рассчитайте начальный капитал u,
обеспечивающий вероятность разорения компании к концу
первого года на уровне 0.01
а)
;
б) 85645;
в)520;
г)170000;
д) 65000
5 баллов
7. Страховщик хочет оценить ожидаемое количество убытков,
λ, для определенного типа полисов. Априорно известно, что λ
имеет Гамма распределение с плотностью
3
где параметры α=2 и β=0.5.
Пусть d означает оценку λ, определим функцию потерь как
определить оптимальную оценку для λ.
а) 0.5;
б) 1.0;
в) 2.0;
г) 4.0;
д) 8.0
7 баллов
8. Случайная переменная X имеет экспоненциальное
распределение с математическим ожиданием 1000.
Индивидуальные размеры убытков определенного типа
страховых договоров, Y, таковы, что
Y=X для 0 < X < 2000
и P(Y=2000)=P(X≥2000) .
Страховщик применяет франшизу величины 100 для убытков
этого типа договоров. Вычислите математическое ожидание
распределения индивидуальных убытков, оплаченных
страховщиком.
а)620,3
б)911,1
в) 769,5
г)317,8
д)199,4
4 балла
9. Вычислите современную стоимость годового аннуитета
пренумерандо на 10 лет так, что размер первого платежа
равен 12, далее 11 и.т.д.
а) 63,78
б) 63,94
в) 64,06
г) 64,23
д) 64,50
3 балла
10. Ожидаемая доходность рыночного портфеля 20%, ставка без
риска 10% годовых. Коэффициент бета акции относительно
рыночного портфеля равен 1,3. Цена акции 15 руб. Инвестор
ожидает, что через год цена акции составит 17,2 руб., и на акцию
будет выплачен дивиденд в 1 руб. Определить, стоит ли инвестору
купить акцию.
а) не стоит покупать
б) стоит купить
в) не имеет значения
3 балла
Всего 49 баллов
Набрано баллов
Процент
4