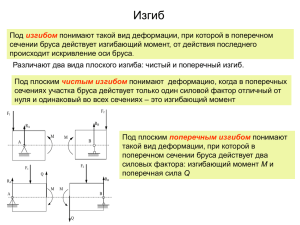
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ 3 Построение эпюр перерезывающих сил и изгибающих
реклама

Прикладная механика Практическое занятие 3 1 ПРАКТИЧЕСКОЕ ЗАНЯТИЕ 3 Построение эпюр перерезывающих сил и изгибающих моментов при изгибе балок Задача 3.1 Построить эпюры перерезывающих сил Q и изгибающих моментов М от сосредоточенных сил F. Проверить дифференцально-интегрвльную зависимость между Q и М. RA F a a a F A a RB B FC Рис. 3.1 Расчётная схема Решение 1. FC F 1) Определяем реакции опор a) MB 0 n Given F a FC 2a F 3a RA 4a Итак, 0 Find RA substituteF C F F 2 1 RA (F) F 2 б) Так как нагружение балки симметричное, то, очевидно, RB (F) RA (F) 2) Строим эпюру поперечных сил Q и эпюру изгибащих моментов М, делая обход балки от опоры слева и справа (рис. 3.2): Прикладная механика RA a Практическое занятие 3 P a a P a A 2 RB B Q 1 P 2 1 P 2 1 Pa 2 1 P 2 1 P 2 M 1 Pa 2 Рис. 3.2 Эпюры поперечных сил и изгибающих моментов ( FÑ 1 F) 2 2. FC 2F 1) Определяем реакции опор a) Given MB n 0 F a FC 2a F 3a RA 4a 0 Find RA substituteF C 2F 0 б) Так как нагружение балки симметричное, то, очевидно, RB (F) RA (F) 2) Строим эпюру поперечных сил Q и эпюру изгибащих моментов М, делая обход балки от опоры слева и справа (рис. 3.3): Нетрудно проверить выполнение дифференциальных зависимостей для балок рис. 3.2 и 3.3 - производная от перерезывающей силы равна величине распределённой нагрузки (она равна нулю и в перевом и во втором случаях), а производная от изгибающего момента по длине балки равна поперечной силе. Прикладная механика RA a F Практическое занятие 3 a F a a A 3 RB B Q 2F F F M Fa Рис. 3.3 Эпюры поперечных сил и изгибающих моментов ( FÑ 2F) Задача 3.2 Построить эпюры перерезывающих сил Q и изгибающих моментов М от сосредоточенных сил F. Проверить дифференцально-интегрвльную зависимость между Q и М. RA F 2F 3F RB a a a a A B Рис. 3.4 Расчётная схема 1. Определяем реакции опор Given 3F a 2F 2a F 3a RA 4a Итак, RA (F) 2.5F Given F a 2F 2a 3F 3a RB 4a RB (F) 3.5F Итак, Решение a) MB n 0 б) Find RA substituteF C MÀ n 0 0 0 7 F Find RB 2 F 5 F 2 Прикладная механика в) Проверка Практическое занятие 3 4 RA (F) RB (F) F 2F 3F 3.5 F 6 F 2.5 F 2) Строим эпюру поперечных сил Q и эпюру изгибащих моментов М, делая обход балки от опоры слева и справа (рис. 3.5): 2.5F a F a 2F a 3F a A 3.5F B 2.5F Q 1.5F 0.5F 3.5F 4Fa 2.5Fa M 3.5Fa Рис. 3.5 Эпюры поперечных сил и изгибающих моментов Задача 3.3 Построить эпюры перерезывающих сил Q и изгибающих моментов М от сосредоточенных сил F. Проверить дифференцально-интегрвльную зависимость между Q и М. F a a a F F Рис. 3.6 Расчётная схема Прикладная механика Практическое занятие 3 5 Решение 1. Для консольной балки можно строить эпюры без определения рекций в заделке. При этом строить эпюры нужно совершая обход балки со свободного (незаделанного) конца балки. Строим эпюры (рис. 3.6): F a F a a Q F F F M 2Fa Fa Рис. 3.7 Эпюры поперечных сил и изгибающих моментов Задача 3.4 Построить эпюры перерезывающих сил Q и изгибающих моментов М для êÍ данной балки (рис. 3.8), если F 60êÍ , M0 50êÍ ì , q 10 , a 2ì . ì Проверить дифференцально-интегрвльную зависимость между Q и М. RA a F a a q RB a В A M0 Рис. 3.8 Расчётная схема Решение Прикладная механика Практическое занятие 3 1. Определяем реакции опор RA 10êÍ a) Given F 2a q 2a 2a M0 RA 3a Итак, MB n 6 0 RA Find RA 0 RA 21.667êÍ RB 10êÍ Given б) F a q 2a a M0 RB 3a MÀ n 0 RB Find RB 0 RB 1.667êÍ в) Проверка RA RB F q 2a 0êÍ Итак, 2) Строим эпюру поперечных сил Q и эпюру изгибащих моментов М, делая обход балки от опоры слева и справа (рис. 3.9): 21.7 кН 2м 60 кН 2м 1.7 кН 2м 2м 10 кН/м В A 50 кНм 60 Q кН 18.3 21.7 1.7 40 41.7 120 M кНм 46.8 50 63.4 80 86.8 Рис. 3.9 Эпюры поперечных сил и изгибающих моментов