КОНВЕКЦИЯ В ПОРИСТОЙ СРЕДЕ ПРИ БОКОВОМ ПРОСАЧИВАНИИ И МОДУЛЯЦИИ СИЛЫ ТЯЖЕСТИ
реклама

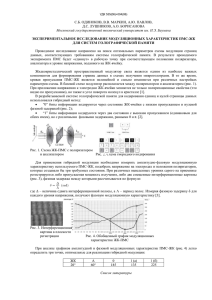
КОНВЕКЦИЯ В ПОРИСТОЙ СРЕДЕ ПРИ БОКОВОМ ПРОСАЧИВАНИИ И МОДУЛЯЦИИ СИЛЫ ТЯЖЕСТИ 1 Д.В. Любимов1, Т.П. Любимова2, Б.С. Марышев2 Пермский государственный национальный исследовательский университет, Пермь 2 Институт механики сплошных сред УрО РАН, Пермь Рассматривается задача о конвекции однокомпонентной жидкости в бесконечном горизонтальном цилиндре прямоугольного сечения, заполненном пористой средой, при подогреве снизу и модуляции силы тяжести. Границы цилиндра считаются идеально теплопроводными, через боковые стенки осуществляется однородное горизонтальное просачивание жидкости. Проводится линейный анализ устойчивости режима однородного горизонтального просачивания по отношению к пространственным возмущениям, слабонелинейный анализ двумерных надкритических режимов. Для случая, когда модуляция отсутствует, обнаружены два типа неустойчивости: монотонная и колебательная. Колебательная неустойчивость реализуется для длинноволновых возмущений, монотонная – для конечных длин волн. В длинноволновом приближении для малых амплитуд модуляции тяжести и скоростей просачивания исследован параметрический резонанс. Найдены границы неустойчивости по отношению к синхронным и субгармоническим возмущениям. Исследование неустойчивости по отношению к возмущениям с конечной длиной волны показало, что при малых амплитудах модуляции наиболее опасными являются пространственные синхронные возмущения с длиной волны порядка нескольких характерных линейных размеров сечения цилиндра. При больших амплитудах модуляции потеря устойчивости при любых значениях волнового числа происходит синхронным образом, причем наиболее опасными являются плоские возмущения. В коротких областях при любых значениях параметров наиболее опасными являются плоские возмущения. Для плоского случая проведен также слабонелинейный анализ. Получена неавтономная двумерная нелинейная система, описывающая динамику конвективного течения. Рис. 1 Характерный вид фазовых портретов двумерной нелинейной системы, описывающей динамику конвективного течения В работе [1] обнаружено, что в случае, когда модуляция и просачивание отсутствуют (Рис. 1а) в системе наблюдается однопараметрическое семейство стационарных решений (каждая фазовая траектория приходит в стационарную точку, принадлежащую окружности). Просачивание приводит к исчезновению стационарных режимов, в фазовом пространстве появляется притягивающий цикл (Рис. 1б) [2]. При наличии просачивания и модуляции тяжести система демонстрирует динамику на торе (Рис.1в). Возникновение тора в расширенном фазовом пространстве обусловлено совокупностью двух причин: наличием собственных колебаний, возникающих при просачивании жидкости, и наличием модуляции. Существование тора обеспечивает условия для синхронизации собственных колебаний с внешней модуляцией (Рис. 1г, случай замкнутой фазовой траектории). Синхронизация исследована с помощью аппарата чисел вращения, получены области синхронизации в пространстве параметров. Найдено, что при отношении высоты поперечного сечения канала к его ширине, кратном 2 4 , в системе наступает вырождение. В этом случае сосуществуют различные устойчивые периодические режимы, образующие однопараметрическое семейство. Реализация того или иного режима происходит в зависимости от начальных условий (на Рис. 1г показана пара периодических режимов, принадлежащих семейству). ЛИТЕРАТУРА. 1. Любимов Д.В., О конвективных движениях в пористой среде, подогреваемой снизу, ПМТФ, 1975, № 2, 131-137 2. Lyubimov D.V., Properties of Thermal Convection in Porous Medium. Instabilities in Multiphase Flows, Plenum Publishing Co., London, 1993