Метод Мора
реклама
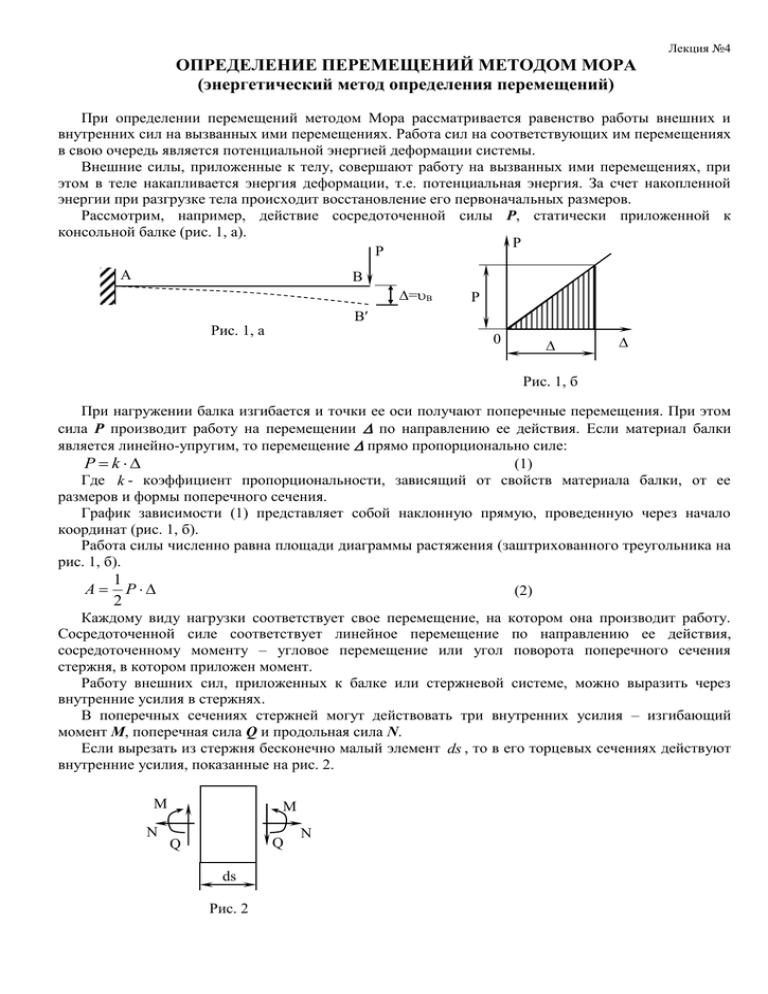
Лекция №4 ОПРЕДЕЛЕНИЕ ПЕРЕМЕЩЕНИЙ МЕТОДОМ МОРА (энергетический метод определения перемещений) При определении перемещений методом Мора рассматривается равенство работы внешних и внутренних сил на вызванных ими перемещениях. Работа сил на соответствующих им перемещениях в свою очередь является потенциальной энергией деформации системы. Внешние силы, приложенные к телу, совершают работу на вызванных ими перемещениях, при этом в теле накапливается энергия деформации, т.е. потенциальная энергия. За счет накопленной энергии при разгрузке тела происходит восстановление его первоначальных размеров. Рассмотрим, например, действие сосредоточенной силы Р, статически приложенной к консольной балке (рис. 1, а). Р Р А В =В Р В Рис. 1, а 0 Рис. 1, б При нагружении балка изгибается и точки ее оси получают поперечные перемещения. При этом сила Р производит работу на перемещении по направлению ее действия. Если материал балки является линейно-упругим, то перемещение прямо пропорционально силе: (1) P k Где k - коэффициент пропорциональности, зависящий от свойств материала балки, от ее размеров и формы поперечного сечения. График зависимости (1) представляет собой наклонную прямую, проведенную через начало координат (рис. 1, б). Работа силы численно равна площади диаграммы растяжения (заштрихованного треугольника на рис. 1, б). A 1 P 2 (2) Каждому виду нагрузки соответствует свое перемещение, на котором она производит работу. Сосредоточенной силе соответствует линейное перемещение по направлению ее действия, сосредоточенному моменту – угловое перемещение или угол поворота поперечного сечения стержня, в котором приложен момент. Работу внешних сил, приложенных к балке или стержневой системе, можно выразить через внутренние усилия в стержнях. В поперечных сечениях стержней могут действовать три внутренних усилия – изгибающий момент М, поперечная сила Q и продольная сила N. Если вырезать из стержня бесконечно малый элемент ds , то в его торцевых сечениях действуют внутренние усилия, показанные на рис. 2. M N M Q Q ds Рис. 2 N Лекция №4 Для каждого элемента внутренние усилия можно рассматривать как внешние нагрузки, производящие работу на соответствующих деформациях элемента. Рассмотрим балку, находящуюся под действием произвольных нагрузок (рис. 3, а). q P А а) С c 1 p P1 1 А б) B B С ℓ Рис. 3 Состояние балки под действием заданных нагрузок назовем грузовым или действительным состоянием. Допустим, требуется определить прогиб балки в некоторой точке С. Приложим в этой точке по направлению искомого перемещения единичную силу P1 1 , т.е. создадим единичное или вспомогательное состояние (рис.3, б). В поперечных сечениях балки действует три внутренних усилия – изгибающий момент М, поперечная сила Q и продольная сила N. Вырежем из балки бесконечно малый элемент ds и рассмотрим действующие в его торцевых сечениях внутренние усилия (рис. 2). Воспользуемся принципом независимости действия сил и вычислим раздельно работу каждого усилия. Введем обозначения: Q p , N p , M p - внешние силы по отношению к элементу ds ; Q1 , N1 , M 1 - внутренние силы по отношению к элементу ds . 1. Продольные силы вызывают взаимные осевые перемещения поперечных сечений (рис. 4), величина которых равна удлинению (укорочению) элемента. ds + d(s) N p – нормальная сила в сечении S, вызванная внешними Nр N1 N1 Nр нагрузками, соответствующими грузовому состоянию системы; d ( s ) – удлинение элемента; N1 – внутреннее продольное усилие в сечении S, вызванное действием единичной силы P1 1 . ds Рис. 4 По закону Гука: d (s) N p ds . EF Работа продольной силы N1 на перемещении d ( s ) равна Лекция №4 AN N1 d (s) N1 N p ds EF E F - жёсткость при растяжении/ сжатии. 0 (3) 0 2. Изгибающие моменты вызывают взаимный поворот поперечных сечений элемента (рис. 5). O M p - изгибающий момент в сечении S, вызванный внешними нагрузками, соответствующими грузовому состоянию системы; M1 - внутренний момент в сечении S, вызванный действием единичной силы P1 1 ; d p - угол взаимного поворота сечений под действием внешних нагрузок, соответствующих грузовому Mр состоянию системы; p - радиус кривизны оси балки под действием внешних нагрузок; O - центр кривизны. dр p Mр M1 M1 ds Рис. 5 Учитывая, что при изгибе балки его нейтральный слой сохраняет свою первоначальную длину, и используя выражение для кривизны изогнутой оси балки (без учета знака) Mp 1 , p E I умножив обе части которого на ds , получим величину угла взаимного поворота сечений ds M p ds d p p EI Работа момента M1 на угловом перемещении d p равна AM M1 d p M1 M p ds EI E I - жесткость при изгибе. 0 (4) 0 3. Поперечные силы вызывают взаимный сдвиг поперечных сечений элемента (рис. 6). dy Q p - поперечная сила в сечении S, вызванная внешними Qр Q1 Q1 Qр нагрузками, соответствующими грузовому состоянию системы; Q1 - внутренне поперечное усилие в сечении S, вызванное действием единичной силы P1 1 ; dy - деформация сдвига. ds Рис. 6 Аналогично выводу формулы (3) получим выражение для определения работы поперечной силы на деформациях сдвига: Лекция №4 AQ k Q1 Qp ds (5) GF где G - модуль упругости материала балки при сдвиге; G F - жёсткость при сдвиге; k - безразмерный коэффициент, зависящий от формы сечения балки и учитывающий неравномерность распределения касательных напряжений по высоте поперечного сечения изгибаемой балки. Например, для прямоугольного сечения k6 5 для круглого сечения k 10 9 для двутаврового сечения k 1 f стенки 0 k 1 ВСЕГДА! 4. Работа внешней единичной силы P1 1 на вызванном ею перемещении 1 p равна A1 p P1 1 p 1 1 p 1 p (6) Применив вариационный принцип Лагранжа (если упругая система находится в равновесии, то суммарная работа всех внешних и внутренних сил на любых малых возможных перемещениях равна нулю), получим A1 p AN AM AQ (7) Подставив выражения (3), (4), (5) и (6) в выражение (7), получим N N M Mp Q Q (8) 1 p 1 p ds 1 ds k 1 p ds EF EI GF 0 0 0 В общем виде выражение (8) будет иметь вид n n n N N M Mp Q Q (9) ip i p dx i dx k i p dx EI GF j 1 0 E F j 1 0 j 1 0 Формула (9) называется формулой Мора. В формуле (9) j 1,2,3...n - номер стержня; - длина стержня; Ni , M i , Qi - внутренние усилия в стержнях, вызванные действием единичной силы Pi 1 или единичного момента M i 1 , прикладываемых по направлению искомого перемещения. В первом случае ip является линейным, а во втором – угловым. усилия в стержнях, соответствующих грузовому состоянию. N p , M p , Qp - возникающие под действием внешних нагрузок, Таким образом, для определения с помощью формулы Мора перемещений в балке или стержневой системе от действия заданных нагрузок производится расчет системы на действие заданных нагрузок и определяются усилия N p , M p , Q p грузового состояния. Затем по направлению искомого перемещения прикладывается единичная сила или единичный момент и определяются вызываемые их действием внутренние усилия Ni , M i , Qi . После чего, выражения для усилий подставляются в формулу (9) и производится интегрирование в пределах длины стержня и суммирование результатов интегрирования по всем стержням системы. Лекция №4 Если в результате вычислений величина ip оказалась положительной, то направление перемещения совпадает с направлением действия единичной нагрузки, а если отрицательной – то оно противоположно этому направлению. АНАЛИЗ МЕТОДА МОРА Для шарнирно-стержневых систем, стержни которых работают на растяжение или сжатие (например, для ферм), отличено от нуля только одно слагаемое формулы Мора: n N N ip i p dx j 1 0 E F При расчете балок и стержневых систем, работающих в основном на изгиб (например, рам), можно с достаточной степенью точности использовать только слагаемое, содержащее изгибающие моменты: n M M p ip i dx EI j 1 0 Для стержней с криволинейной осью интегрирование в формуле Мора должно производиться по длине дуги оси стержня. ВЫЧИСЛЕНИЕ ИНТЕГРАЛА МОРА ПЕРЕМНОЖЕНИЕМ ЭПЮР ПО ПРАВИЛУ А.К. ВЕРЕЩАГИНА Для балок и стержневых систем, состоящих из прямых стержней, внутренние усилия единичных состояний Ni , M i , Qi являются линейными функциями или на протяжении каждого стержня или на его отдельных участках. Внутренние усилия грузового состояния N p , M p , Q p могут иметь произвольные законы изменения по длине стержней. Если балки и стержни имеют при этом постоянные или ступенчато постоянные жесткости E F , E I , G F , то вычисление интегралов в формуле Мора может быть произведено с помощью эпюр внутренних усилий. Рассмотрим, например, эпюры изгибающих моментов M p и M i в прямом стержне постоянной жесткости (рис. 7). y d ( x) dx (x) Грузовая эпюра С x функция, а единичная является линейной. dx xc 0 с ℓ a b Рис. 7 M p (x) - (x) x произвольная эпюра M i (x) Лекция №4 b ip a Mi M p EI b dx ( x) ( x)dx (10) a АЛГОРИТМ ВЫВОДА 1. Строим графики функций (x ) и (x) . 2. На графике функции (x ) выделим элементарную полоску d , площадь которой будет равна ( x) dx . 3. На графике функции (x) покажем ординату c , расположенную под центром тяжести фигуры, образованной функцией (x ) , горизонтальной осью и прямыми x a и x b . Если функция (x) имеет вид ( x) mx n , то c mxc n 4. Подставим в выражение (10) выражение ( x) mx n и получим b b b b b a a a a a ip [mx n] ( x)dx m ( x) x dx n ( x)dx m xd n d m S y n Таким образом, получили ip m S y n Так как S y xc , то ip m S y n m xc n (m xc n) c Т.е. ip c . Таким образом, интеграл от произведения двух функций равен произведению площади криволинейной эпюры и ординаты прямолинейной, расположенной под центром тяжести криволинейной эпюры. Результат «перемножения» однозначных эпюр является положительным, а разнозначных – отрицательным. При использовании правила А.К. Верещагина сложные эпюры необходимо разбить на простые фигуры, у которых известны площадь и положение центра тяжести. Результат «перемножения» двух трапеций (рис.8) можно представить в виде следующей формулы: (2ac 2bd ad bc) . 6 b a c d ℓ Рис. 8 Правило Верещагина нельзя применять в случае, когда обе эпюры являются нелинейными (например, для стержней с криволинейной осью). В этом случае при определении перемещений методом Мора производится аналитическое или численное вычисление интегралов в формуле (9). Лекция №4 ПРИМЕР РАСЧЕТА ПЕРЕМЕЩЕНИЙ МЕТОДОМ МОРА Дано: q A B ℓ q 2 2 1 q 2 q 3 3 2 6 Mp Найти: 1. Определить вертикальные перемещения точки В. 2. Определить угловое перемещение (угол поворота) в точке В. Используемые обозначения: M1 - момент от единичной безразмерной силы; Mp - момент от нагрузки (грузовой момент); 1 p - вертикальное перемещение в точке В; 2 p - угол поворота в точке В. X1 1 3 4 ℓ M1 4 X2 1 1 1 M2 1 p M1 M p dx EI 1 q 2 q 3 - площадь криволинейной эпюры 3 2 6 3 B - ордината прямолинейной эпюры. 4 Значит q 3 3 q 4 1 p B 6 4 8 M Mp 2 p 2 dx EI 2 p B q 3 q 3 1 6 6


