ФМЭ 1 курс магистратуры, 2010-2011 Микро-3
реклама

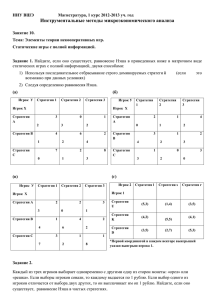
ФМЭ 1 курс магистратуры, 2010-2011 Микро-3 Семинар 19. Тема. Теория игр. Олигополия. Задача 1. Матрица игры имеет следующий вид: Игрок 1 Стратегия 1 Игрок 2 Стратегия А 2, 3 Стратегия В 1, 4 Стратегия С 0, 7 Стратегия 2 3, 0 2, 6 1, 2 Стратегия 3 2, 1 4, 2 3, 8 Найдите равновесие по Нэшу путем последовательного исключения строго доминируемых стратегий. Задача 2. В игре участвуют пешеход и автомобилист. Каждый из игроков имеет две стратегии: проявлять осторожность и не проявлять осторожности. От выбранных стратегий зависит вероятность дорожно-транспортного происшествия (автомобилист собьет пешехода). Если оба ведут себя неосторожно, то вероятность происшествия равна 1/2, если только один ведет себя неосторожно, то вероятность равна 1/10, а если оба осторожны, то вероятность равна 1/100. В случае, если произойдет столкновение, то ущерб пешехода в неких условных единицах составит 1000, а ущерб автомобилиста—200. Кроме того, осторожное поведение на дороге связано для обоих игроков с издержками, равными 100. (а) Запишите игру в нормальной форме; (б) Найдите равновесие по Нэшу. Задача 3. Заполните пропущенные выигрыши в следующей таблице так, чтобы в получившейся игре: а) не было ни одного равновесия Нэша, 1\2 L R б) было одно равновесие Нэша, T ?, 1 2, ? в) было два равновесия Нэша, M 4, ? ?, 0 г) было три равновесия Нэша, д) было четыре равновесия Нэша. Задача 4. Рассмотрите отрасль, в которой N фирм, производящих однородную продукцию, конкурируют по Курно. Предположим, что все фирмы имеют одинаковые постоянные предельные издержки c 0 . Обратная функция совокупного спроса на продукцию отрасли имеет вид: p (Q ) a bQ , причем a c , b 0 . Предположим, в отрасли вводится налог на производство каждой единицы продукции, равный t , причём a c t . Как изменится равновесная цена продукции в результате введения налога? Задача 5. Рыночная функция спроса (обратная) задана P 70 Q , где Q - агрегированный выпуск продукции. Две фирмы, производящие однородный товар, имеют равные предельные издержки $10. 1) Найдите равновесие Курно на этом рынке. Каковы прибыли фирм? Рассмотрите также вариант, когда по каким-либо причинам выпуск второй фирмой снижается до 10 единиц продукции. найдите цену продукции и прибыли фирм. 2)Будет ли равновесие Курно устойчивым? ФМЭ 1 курс магистратуры, 2010-2011 Микро-3 Семинар 19. Тема. Теория игр. Олигополия. Задача 1. Матрица игры имеет следующий вид: Игрок 1 Стратегия 1 Игрок 2 Стратегия А 2, 3 Стратегия В 1, 4 Стратегия С 0, 7 Стратегия 2 3, 0 2, 6 1, 2 Стратегия 3 2, 1 4, 2 3, 8 Найдите равновесие по Нэшу путем последовательного исключения строго доминируемых стратегий. Задача 2. В игре участвуют пешеход и автомобилист. Каждый из игроков имеет две стратегии: проявлять осторожность и не проявлять осторожности. От выбранных стратегий зависит вероятность дорожно-транспортного происшествия (автомобилист собьет пешехода). Если оба ведут себя неосторожно, то вероятность происшествия равна 1/2, если только один ведет себя неосторожно, то вероятность равна 1/10, а если оба осторожны, то вероятность равна 1/100. В случае, если произойдет столкновение, то ущерб пешехода в неких условных единицах составит 1000, а ущерб автомобилиста—200. Кроме того, осторожное поведение на дороге связано для обоих игроков с издержками, равными 100. (а) Запишите игру в нормальной форме; (б) Найдите равновесие по Нэшу. Задача 3. Заполните пропущенные выигрыши в следующей таблице так, чтобы в получившейся игре: а) не было ни одного равновесия Нэша, 1\2 L R б) было одно равновесие Нэша, T ?, 1 2, ? в) было два равновесия Нэша, M 4, ? ?, 0 г) было три равновесия Нэша, д) было четыре равновесия Нэша. Задача 4. Рассмотрите отрасль, в которой N фирм, производящих однородную продукцию, конкурируют по Курно. Предположим, что все фирмы имеют одинаковые постоянные предельные издержки c 0 . Обратная функция совокупного спроса на продукцию отрасли имеет вид: p (Q ) a bQ , причем a c , b 0 . Предположим, в отрасли вводится налог на производство каждой единицы продукции, равный t , причём a c t . Как изменится равновесная цена продукции в результате введения налога? Задача 5. Рыночная функция спроса (обратная) задана P 70 Q , где Q - агрегированный выпуск продукции. Две фирмы, производящие однородный товар, имеют равные предельные издержки $10. 1) Найдите равновесие Курно на этом рынке. Каковы прибыли фирм? Рассмотрите также вариант, когда по каким-либо причинам выпуск второй фирмой снижается до 10 единиц продукции. найдите цену продукции и прибыли фирм. 2)Будет ли равновесие Курно устойчивым?