Лабораторная работа №2 "
реклама
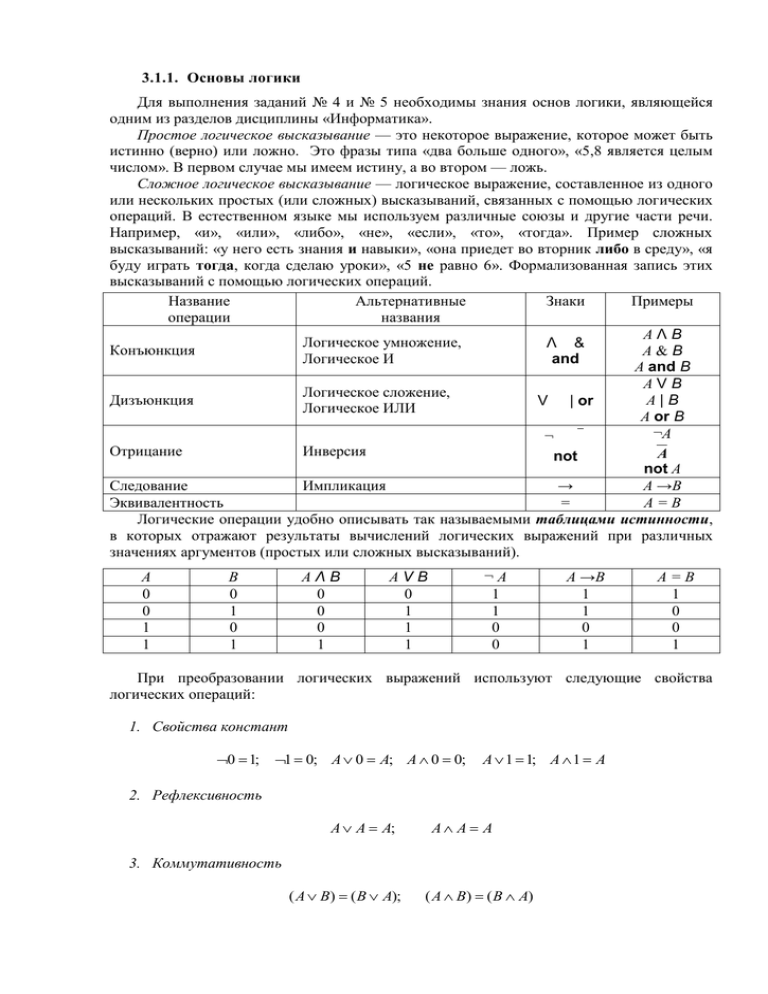
3.1.1. Основы логики Для выполнения заданий № 4 и № 5 необходимы знания основ логики, являющейся одним из разделов дисциплины «Информатика». Простое логическое высказывание — это некоторое выражение, которое может быть истинно (верно) или ложно. Это фразы типа «два больше одного», «5,8 является целым числом». В первом случае мы имеем истину, а во втором — ложь. Сложное логическое высказывание — логическое выражение, составленное из одного или нескольких простых (или сложных) высказываний, связанных с помощью логических операций. В естественном языке мы используем различные союзы и другие части речи. Например, «и», «или», «либо», «не», «если», «то», «тогда». Пример сложных высказываний: «у него есть знания и навыки», «она приедет во вторник либо в среду», «я буду играть тогда, когда сделаю уроки», «5 не равно 6». Формализованная запись этих высказываний с помощью логических операций. Название Альтернативные Знаки Примеры операции названия AΛB Логическое умножение, Λ & Конъюнкция A&B Логическое И and A and B AVB Логическое сложение, Дизъюнкция A|B V | or Логическое ИЛИ A or B ¬A ¬ Отрицание Инверсия A not not A Следование Импликация → A →B Эквивалентность = A=B Логические операции удобно описывать так называемыми таблицами истинности, в которых отражают результаты вычислений логических выражений при различных значениях аргументов (простых или сложных высказываний). A 0 0 1 1 AΛB 0 0 0 1 B 0 1 0 1 AVB 0 1 1 1 ¬A 1 1 0 0 A →B 1 1 0 1 A=B 1 0 0 1 При преобразовании логических выражений используют следующие свойства логических операций: 1. Свойства констант 0 1; 1 0; A 0 A; A 0 0; A 1 1; A 1 A 2. Рефлексивность A A A; A A A 3. Коммутативность ( A B) ( B A); ( A B) ( B A) 4. Ассоциативность ( A B) С A ( B C ); ( A B) C A ( B C ) 5. Дистрибутивность ( A ( B С ) ( A B) ( A C ); A ( B C ) ( A B) ( А C ) 6. Закон отрицания (двойного отрицания) (A) A 7. Законы де Моргана ( A B) A B; ( A B) A B 8. Законы поглощения A ( A B) A; A ( A B) A Также вводятся дополнительные операции: импликация: A → B = (¬A V B); эквивалентность: (A = B) = (A Λ B) V (¬A Λ ¬B). 3.1.2. Примеры решения логических задач 1) Запишите интервал значений X, для которых истинно высказывание: (( X 5)) ( X 6)) РЕШЕНИЕ Введем обозначения: A = X > 5; B = X > 6. Тогда высказывание примет вид ¬ (A → B). Составим для этого высказывания таблицу истинности: A B A→B ¬ (A → B) 0 0 1 0 0 1 1 0 0 1 0 1 1 1 1 0 Высказывание истинно, если A истинно, а B ложно. Следовательно, если рассматривать действительные числа, то интервал значений Х равен: 5 X 6 . Для целых чисел: Х=6. 2) Укажите, какое логическое выражение равносильно выражению A (B C ) . 1) A B C 2) A B C 3) A B C 4) A B C РЕШЕНИЕ Преобразуем исходное выражение A (B C ) : а) применив закон де Моргана к выражению в скобках, получаем: A ( B C ) б) используя закон двойного отрицания, получаем: A ( B C ) Следовательно, ответ: 3. 3) На числовой прямой даны два отрезка: P = [2, 10] и Q = [6, 14]. Выберите такой отрезок A, что формула ( (x А) → (x P) ) \/ (x Q) тождественно истинна, то есть принимает значение 1 при любом значении переменной х. 1) [0, 3] 2) [3, 11] 3) [11, 15] 4) [15, 17] РЕШЕНИЕ 1) Введем обозначение: A: x А, P: x P, Q: x Q. Тогда высказывание примет вид: Z = (A→P) \/ Q 2) Представим импликацию A → P через операции «\/» и «»: (A→P) =A \/ P. В результате получаем Z = A \/ P \/ Q. Выражение Z истинно во всех случаях, кроме одного, когда все аргументы ложны. Следовательно, выражение Z = A \/ P \/ Q ложно при A = 1, P = 0, Q = 0. Поэтому если область истинности A выйдет за пределы отрезка [2,14], где одновременно ложны P и Q, то Z = (A→P) \/ Q будет ложно. Это значит, что A может быть истинно только внутри отрезка [2,14]. Из всех отрезков, приведенных в условии, только отрезок [3,11] (вариант 2) находится целиком внутри отрезка [2,14], это и есть правильный ответ. 3) Ответ: 2. 3.1.3. Задания 1. Каково наибольшее целое число X, при котором истинно высказывание (50 < X·X) → (50 > (X+1) ∙ (X+1))? 2. Для какого из указанных значений числа X истинно высказывание ((X < 5)→(X < 3)) ((X < 2)→(X < 1)) 1) 1 2) 2 3) 3 4) 4 3. Для какого числа X истинно высказывание ((X > 3)(X < 3)) →(X < 1) 1) 1 2) 2 3) 3 4) 4 4. Для какого числа X истинно высказывание X > 1 ((X < 5)→(X < 3)) 1) 1 2) 2 3) 3 4) 4 5. Для какого имени истинно высказывание ¬ (Первая буква имени гласная → Четвертая буква имени согласная)? 1) ЕЛЕНА 2) ВАДИМ 3) АНТОН 4) ФЕДОР 6. Для какого символьного выражения неверно высказывание: Первая буква гласная → ¬ (Третья буква согласная)? 1) abedc 2) becde 3) babas 7. Для какого числа X истинно высказывание 4) abcab (X > 2)(X > 5)→(X < 3) 1) 5 2) 2 3) 3 4) 4 8. Для какого из значений числа Z высказывание ((Z > 2)(Z > 4)) →(Z > 3) будет ложным? 1) 1 2) 2 3) 3 4) 4 9. Для какого имени истинно высказывание: ¬ (Первая буква имени согласная → Третья буква имени гласная)? 1) ЮЛИЯ 2) ПЕТР 3) АЛЕКСЕЙ 4) КСЕНИЯ 10. На числовой прямой даны два отрезка: P = [2, 20] и Q = [15, 25]. Выберите такой отрезок A, что формула ( (x А) → (x P) ) \/ (x Q) тождественно истинна, то есть принимает значение 1 при любом значении переменной х. 1) [0, 15] 2) [10, 25] 3) [2, 10] 4) [15, 20] 11. На числовой прямой даны три отрезка: P = [10, 25], Q = [15, 30] и R=[25,40]. Выберите такой отрезок A, что формула ( (x Q) → (x R) ) /\ (x A) /\ (x P) тождественно ложна, то есть принимает значение 0 при любом значении переменной х. 1) [0, 15] 2) [10, 40] 3) [25, 35] 4) [15, 25] 12. На числовой прямой даны два отрезка: P = [5, 15] и Q = [12, 18]. Выберите такой отрезок A, что формула ( (x А) → (x P) ) \/ (x Q) тождественно истинна, то есть принимает значение 1 при любом значении переменной х. 1) [3, 11] 2) [2, 21] 3) [10, 17] 4) [15, 20] 13. На числовой прямой даны два отрезка: P = [5, 10] и Q = [15, 18]. Выберите такой отрезок A, что формула ( (x А) → (x P) ) \/ (x Q) тождественно истинна, то есть принимает значение 1 при любом значении переменной х. 1) [3, 11] 2) [6, 10] 3) [8, 16] 4) [17, 23] 14. На числовой прямой даны два отрезка: P = [25, 30] и Q = [15, 20]. Выберите такой отрезок A, что формула ( (x А) → (x P) ) \/ (x Q) тождественно истинна, то есть принимает значение 1 при любом значении переменной х. 1) [10, 15] 2) [12, 30] 3) [20, 25] 4) [26, 28] 15. На числовой прямой даны два отрезка: P = [2, 20] и Q = [15, 30]. Выберите такой отрезок A, что формула ( (x А) → (x P) ) \/ (x Q) тождественно истинна, то есть принимает значение 1 при любом значении переменной х. 1) [0, 15] 2) [3, 20] 3) [10, 25] 4) [25, 40]






