Концепция функции полезности

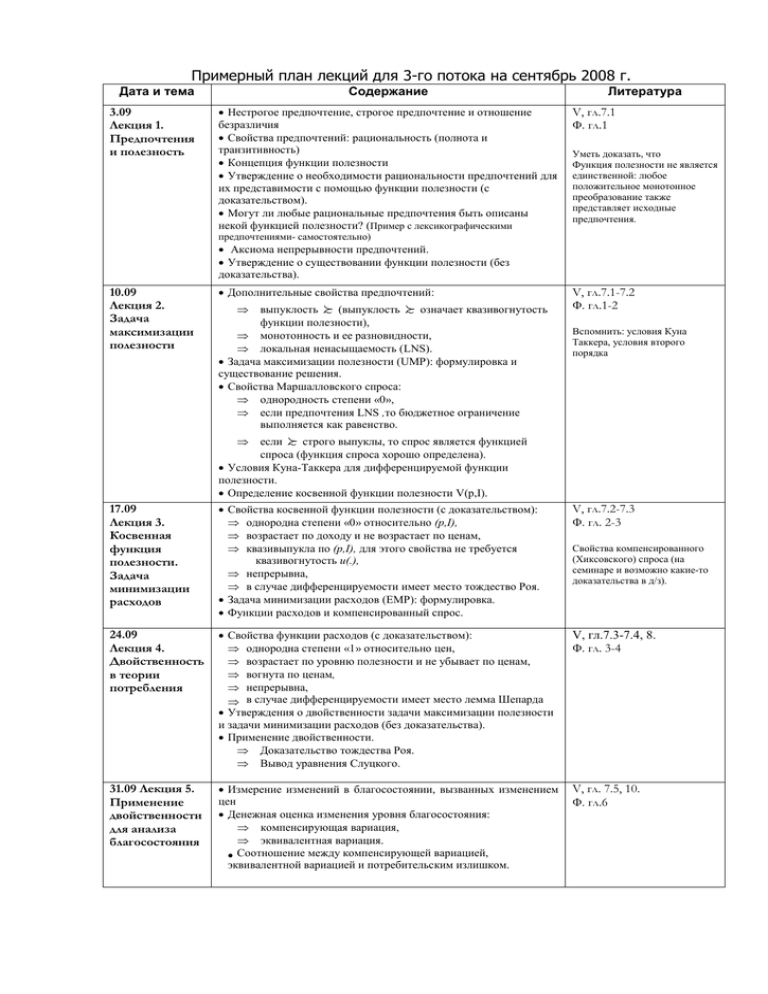
Примерный план лекций для 3-го потока на сентябрь 2008 г.
Дата и тема
3.09
Лекция 1.
Предпочтения
и полезность
Содержание
 Нестрогое предпочтение, строгое предпочтение и отношение
безразличия
 Свойства предпочтений: рациональность (полнота и
транзитивность)
 Концепция функции полезности
 Утверждение о необходимости рациональности предпочтений для
их представимости с помощью функции полезности (с
доказательством).
 Могут ли любые рациональные предпочтения быть описаны
некой функцией полезности? (Пример с лексикографическими
Литература
V, гл.7.1
Ф. гл.1
Уметь доказать, что
Функция полезности не является
единственной: любое
положительное монотонное
преобразование также
представляет исходные
предпочтения.
предпочтениями- самостоятельно)
 Аксиома непрерывности предпочтений.
 Утверждение о существовании функции полезности (без
доказательства).
10.09
Лекция 2.
Задача
максимизации
полезности
 Дополнительные свойства предпочтений:
выпуклость ~
 (выпуклость ~
 означает квазивогнутость
функции полезности),
 монотонность и ее разновидности,
 локальная ненасыщаемость (LNS).
 Задача максимизации полезности (UMP): формулировка и
существование решения.
 Свойства Маршалловского спроса:
 однородность степени «0»,
 если предпочтения LNS ,то бюджетное ограничение
выполняется как равенство.

V, гл.7.1-7.2
Ф. гл.1-2
Вспомнить: условия Куна
Таккера, условия второго
порядка
если ~
 строго выпуклы, то спрос является функцией
спроса (функция спроса хорошо определена).
 Условия Куна-Таккера для дифференцируемой функции
полезности.
 Определение косвенной функции полезности V(p,I).

17.09
Лекция 3.
Косвенная
функция
полезности.
Задача
минимизации
расходов
 Свойства косвенной функции полезности (с доказательством):
 однородна степени «0» относительно (p,I),
 возрастает по доходу и не возрастает по ценам,
 квазивыпукла по (p,I), для этого свойства не требуется
квазивогнутость u(.),
 непрерывна,
 в случае дифференцируемости имеет место тождество Роя.
 Задача минимизации расходов (EMP): формулировка.
 Функции расходов и компенсированный спрос.
V, гл.7.2-7.3
Ф. гл. 2-3
24.09
Лекция 4.
Двойственность
в теории
потребления
 Свойства функции расходов (с доказательством):
 однородна степени «1» относительно цен,
 возрастает по уровню полезности и не убывает по ценам,
 вогнута по ценам,
 непрерывна,
 в случае дифференцируемости имеет место лемма Шепарда
 Утверждения о двойственности задачи максимизации полезности
и задачи минимизации расходов (без доказательства).
 Применение двойственности.
 Доказательство тождества Роя.
 Вывод уравнения Слуцкого.
V, гл.7.3-7.4, 8.
Ф. гл. 3-4
31.09 Лекция 5.
Применение
двойственности
для анализа
благосостояния
 Измерение изменений в благосостоянии, вызванных изменением
цен
 Денежная оценка изменения уровня благосостояния:
 компенсирующая вариация,
 эквивалентная вариация.
 Соотношение между компенсирующей вариацией,
эквивалентной вариацией и потребительским излишком.
V, гл. 7.5, 10.
Ф. гл.6
Свойства компенсированного
(Хиксовского) спроса (на
семинаре и возможно какие-то
доказательства в д/з).