Тема 8: Теория выбора в условиях неопределенности

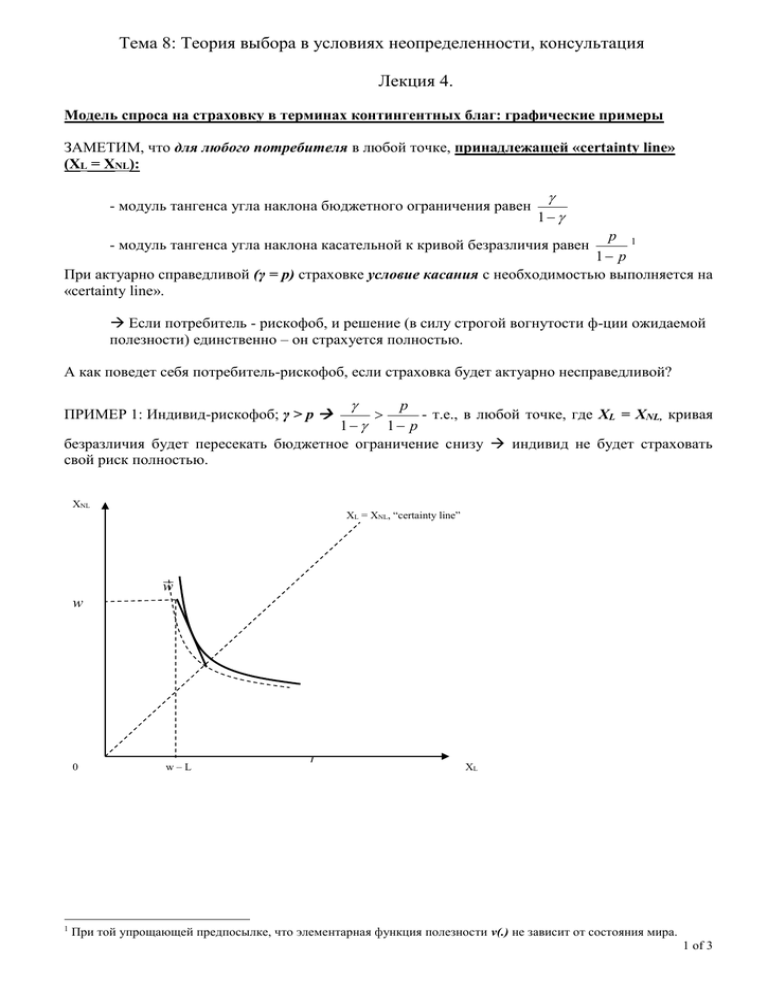
Тема 8: Теория выбора в условиях неопределенности, консультация
Лекция 4.
Модель спроса на страховку в терминах контингентных благ: графические примеры
ЗАМЕТИМ, что для любого потребителя в любой точке, принадлежащей «certainty line»
(XL = XNL):
- модуль тангенса угла наклона бюджетного ограничения равен

1 
p 1
1 p
При актуарно справедливой (γ = p) страховке условие касания с необходимостью выполняется на
«certainty line».
- модуль тангенса угла наклона касательной к кривой безразличия равен
 Если потребитель - рискофоб, и решение (в силу строгой вогнутости ф-ции ожидаемой
полезности) единственно – он страхуется полностью.
А как поведет себя потребитель-рискофоб, если страховка будет актуарно несправедливой?

p
- т.е., в любой точке, где XL = XNL, кривая
1  1 p
безразличия будет пересекать бюджетное ограничение снизу  индивид не будет страховать
свой риск полностью.
ПРИМЕР 1: Индивид-рискофоб; γ > p 

XNL
XL = XNL, “certainty line”
w
w
0
1
w–L
XL
При той упрощающей предпосылке, что элементарная функция полезности v(.) не зависит от состояния мира.
1 of 3
ПРИМЕР 2: Индивид-рискофил; страховка актуарно справедлива:
XNL
XL = XNL, “certainty line”
w
w
w–L
0
XL
ПРИМЕР 3: Индивид – риск-нейтрал, страховка актуарно несправедлива (γ > p)
XNL
XL = XNL, “certainty line”
w
w
U  pv( X L )  (1  p)v( X NL )
0
w–L
XL
Контингентные блага: спрос на рисковый актив
- индивид-рискофоб, предпочтения описываются функцией ожидаемой
элементарная функция полезности v(.) не зависит от состояния мира
- возможны два состояния мира:
- с вероятностью p  (0; 1) наступает экономический рост (B, boom)
- с вероятностью (1 – p) наступает экономический кризис (S, slump)
полезности,
- первоначальное богатство индивида составляет w
- индивиду доступны 2 актива:
- актив 1 (безрисковый): вложив а, вы получаете a в любом состоянии мира
- актив 2 (рисковый): вложив a, вы получаете:
- аc > a
в состоянии мира B
- аd < a,
в состоянии мира S
2 of 3
Предположим, индивид вкладывает a долларов в рисковый актив. В терминах контингентных
благ его бюджетное ограничение описывается следующей системой уравнений:
X B  ac  w  a 
 X S (c  1)  X B (1  d )  w(c  1)  w(1  d )



X

ad

w

a
 S
Задача потребителя:
max pv( X B )  (1  p)v( X S )
XB ,XS
s.t.
X S (c  1)  X B (1  d )  w(c  1)  w(1  d )
Учитывая, что функция полезности рискофоба строго вогнута, задача потребителя может иметь 3
типа решений. Проиллюстрируем их графически:
XB
Угловые решения
XB = XS, “risk-free line”
Внутреннее решение
wc
w
w
0
wd
w
XS
Угловое решение (w; w) соответствует ситуации, когда потребитель вкладывает все свое богатство в
безрисковый актив. И наоборот, угловое решение (wc; wd) соответствует ситуации, когда потребитель
вкладывает все свое богатство в рисковый актив
(тогда в благоприятном состоянии мира он получает wc > w, а в неблагоприятном: wd < w).
? При каких условиях рискофоб будет инвестировать положительную сумму в рисковый актив?
Для этого кривая безразличия, проходящая через точку w , должна иметь в этой точке меньший
наклон, чем бюджетное ограничение, то есть:
MRS XS , XB
XS  XB  w

(1  p )v' ( w) (1  p ) c  1
(1  p ) c  1




 1  d  p  pd  pc  p 
pv' ( w)
p
1 d
p
1 d
 1  pc  (1  p )d
Последнее неравенство означает, что ожидаемый доход на 1 доллар, вложенный в рисковый
актив, должен превышать ожидаемый доход на 1 доллар, вложенный в безрисковый актив.
3 of 3