11 класс.
реклама
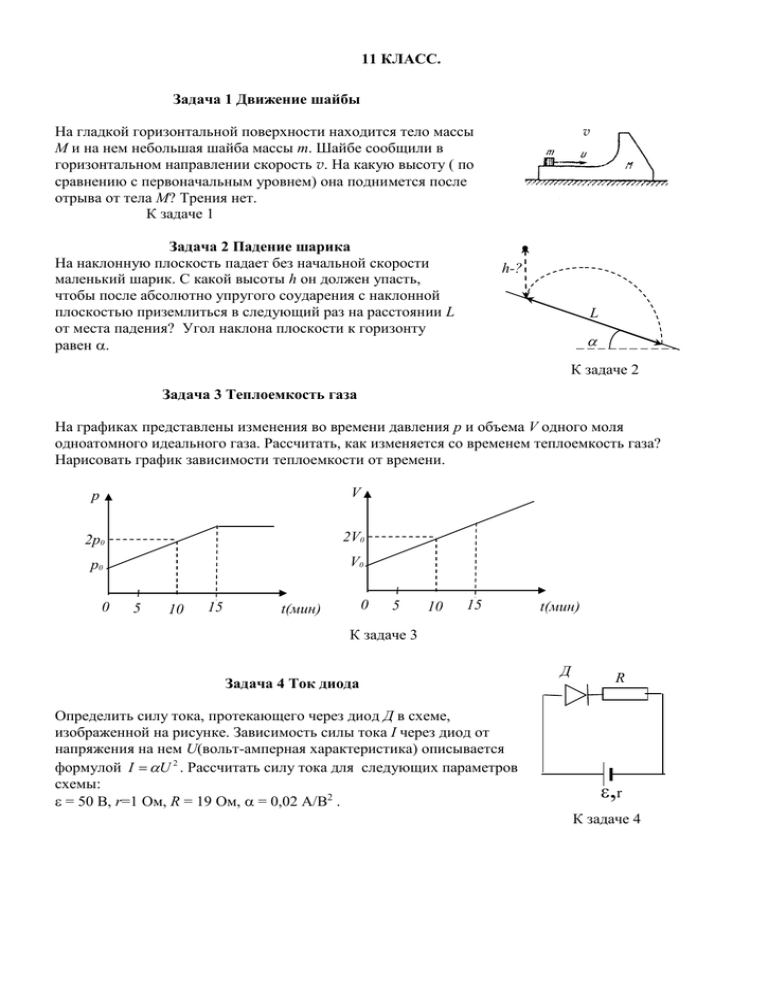
11 КЛАСС. Задача 1 Движение шайбы v На гладкой горизонтальной поверхности находится тело массы М и на нем небольшая шайба массы m. Шайбе сообщили в горизонтальном направлении скорость v. На какую высоту ( по сравнению с первоначальным уровнем) она поднимется после отрыва от тела М? Трения нет. К задаче 1 h-? Задача 2 Падение шарика На наклонную плоскость падает без начальной скорости маленький шарик. С какой высоты h он должен упасть, чтобы после абсолютно упругого соударения с наклонной плоскостью приземлиться в следующий раз на расстоянии L от места падения? Угол наклона плоскости к горизонту равен . L К задаче 2 Задача 3 Теплоемкость газа На графиках представлены изменения во времени давления p и объема V одного моля одноатомного идеального газа. Рассчитать, как изменяется со временем теплоемкость газа? Нарисовать график зависимости теплоемкости от времени. p V 2p0 2V0 p0 V0 0 5 10 15 0 t(мин) 5 10 15 t(мин) К задаче 3 Задача 4 Ток диода Определить силу тока, протекающего через диод Д в схеме, изображенной на рисунке. Зависимость силы тока I через диод от напряжения на нем U(вольт-амперная характеристика) описывается формулой I U 2 . Рассчитать силу тока для следующих параметров схемы: = 50 В, r=1 Ом, R = 19 Ом, = 0,02 А/В2 . Д R ,r К задаче 4 Решения. Задача 1 Движение шайбы 1. В горизонтальном направлении на систему внешние силы не действуют, следовательно, сохраняется горизонтальная проекция импульса: mv = (M + m)u 2. Трения нет, значит, сохраняется полная механическая энергия системы: 2 mv 2 M m u mgh 2 2 3. Решая совместно оба уравнения, получим: v2 M h 2g M m Критерии оценивания 1. Закон сохранения горизонтальной проекции импульса: 2. Закон сохранения энергии 3. Решение системы, вывод результата 3 3 4 Задача 2 Падение шарика 1. Скорость шарика в момент первого столкновения с плоскостью v0 2gh 2. Дальнейшее движение шарика есть движение тела, брошенного под углом =/2 - 2 к горизонту, т.к. угол падения при абсолютно упругом соударении равен углу отражения. 3. Выберем начало системы координат в точке первого столкновения. Тогда уравнение gx 2 траектории шарика: y x tg . 2v0 cos 2 4. Координаты точки при втором столкновении x L cos ; y L sin . 5. Тогда уравнение траектории дает L sin L cos ctg 2 gL2 2v0 sin 2 2 gL cos 2 2sin 2 2 ctg 2 cos sin 7. Выражая из последнего уравнения h и преобразуя тригонометрическое выражение, L получаем h 8sin 6. Откуда v02 2 gh Критерии оценивания 1.Скорость в конце свободного падения 2. Определение угла отскока к горизонту шарика 3. Написано уравнение траектории (или правильно написаны законы движения по осям) с указанием координат конечной точки) 4. Получено выражение для v02 или h (без преобразований) (пункт 6) 5. Получен окончательный ответ (пункт 7) 1 1 4 1 3 Задача 3 Теплоемкость газа 1. В интервале от 0 до 15 минут газ участвует в процессе, при котором p p0 V V0 2. По первому закону термодинамики p 2 p0 3 Q C T U A 2 p0 2V0 p0V0 0 2V0 V0 6 p0V0 2 2 3. Из уравнения Менделеева-Клапейрона 2 p0 2V0 p0V0 3 p0V0 RT 4. Тогда теплоемкость газа в интервале от 0 до 15 минут C 2R 5 5. В дальнейшем – процесс изобарический и C R 2 Критерии оценивания 1.Получено уравнение процесса (пункт 1) 2. Определено изменение внутренней энергии 3. Рассчитана работа газа 4. Вычислена теплоемкость на первом этапе 5. Теплоемкость при изобарическом процессе 6. График С(t) 2 2 2 2 1 1 Задача 4 Ток диода 1. Закон Ома I R r U U 2 R r U 2. Решение квадратного уравнения 1 1 4 ( R r ) U 5B 2 ( R r ) (отрицательный знак перед корнем смысла не имеет) 3.Тогда сила тока равна I U 2 0.5 A Критерии оценивания 1. Закон Ома с подставленным значением тока 2. Решение квадратного уравнения 1) 3. Отбрасывание знака «минус» перед корнем 4. Вычислено значение U 5. Найдена величина тока в цепи 2 4 1 2 1



