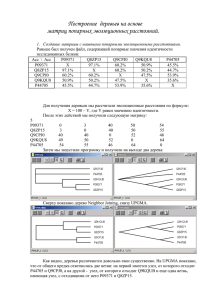
16. Операции вставки/удаления в дереве. Вставка:
реклама
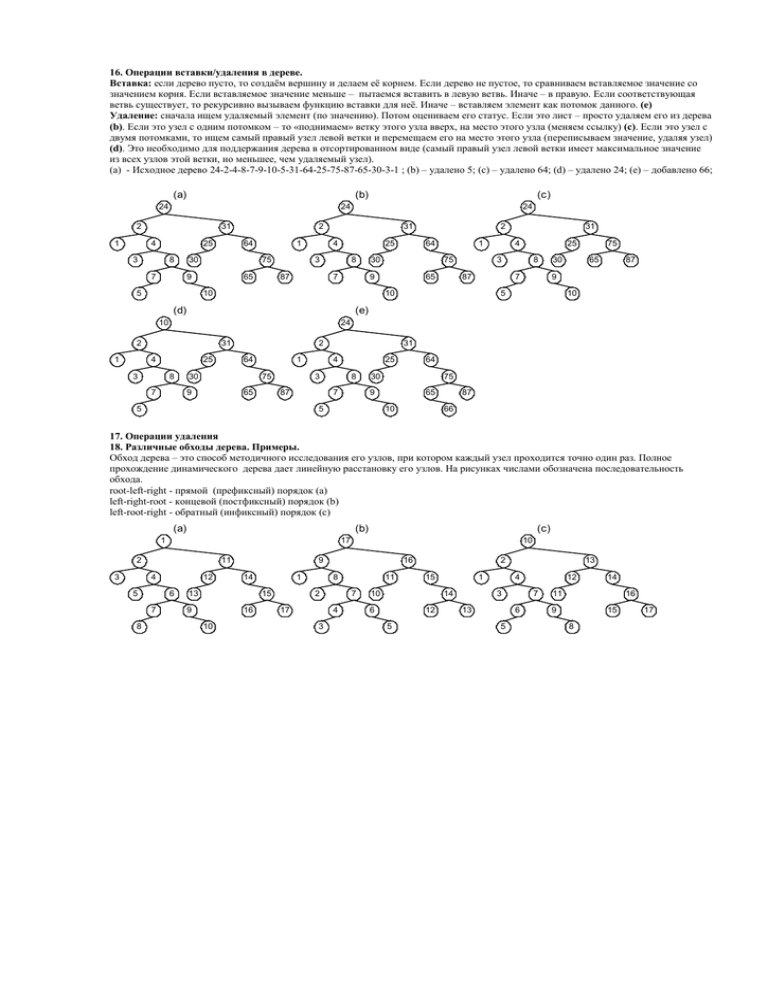
16. Операции вставки/удаления в дереве. Вставка: если дерево пусто, то создаём вершину и делаем её корнем. Если дерево не пустое, то сравниваем вставляемое значение со значением корня. Если вставляемое значение меньше – пытаемся вставить в левую ветвь. Иначе – в правую. Если соответствующая ветвь существует, то рекурсивно вызываем функцию вставки для неё. Иначе – вставляем элемент как потомок данного. (e) Удаление: сначала ищем удаляемый элемент (по значению). Потом оцениваем его статус. Если это лист – просто удаляем его из дерева (b). Если это узел с одним потомком – то «поднимаем» ветку этого узла вверх, на место этого узла (меняем ссылку) (c). Если это узел с двумя потомками, то ищем самый правый узел левой ветки и перемещаем его на место этого узла (переписываем значение, удаляя узел) (d). Это необходимо для поддержания дерева в отсортированном виде (самый правый узел левой ветки имеет максимальное значение из всех узлов этой ветки, но меньшее, чем удаляемый узел). (a) - Исходное дерево 24-2-4-8-7-9-10-5-31-64-25-75-87-65-30-3-1 ; (b) – удалено 5; (c) – удалено 64; (d) – удалено 24; (e) – добавлено 66; (a) (b) 24 2 1 31 4 25 3 8 7 64 1 75 9 24 2 30 5 65 31 4 25 3 87 8 7 64 1 75 9 65 31 4 25 3 87 8 7 10 (d) 30 75 65 87 9 5 10 (e) 24 2 31 4 25 3 2 30 10 10 1 (c) 24 8 7 2 64 30 1 75 9 65 31 4 25 3 87 8 7 5 64 30 75 9 5 65 10 87 66 17. Операции удаления 18. Различные обходы дерева. Примеры. Обход дерева – это способ методичного исследования его узлов, при котором каждый узел проходится точно один раз. Полное прохождение динамического дерева дает линейную расстановку его узлов. На рисунках числами обозначена последовательность обхода. root-left-right - прямой (префиксный) порядок (a) left-right-root - концевой (постфиксный) порядок (b) left-root-right - обратный (инфиксный) порядок (c) (a) (b) 1 2 3 11 4 5 8 12 6 7 (c) 17 9 14 13 1 15 9 16 10 10 16 8 2 17 7 4 3 11 2 15 10 1 14 6 12 5 13 4 3 13 7 6 5 12 14 11 16 9 15 8 17