ФВ и законы Излуч
реклама
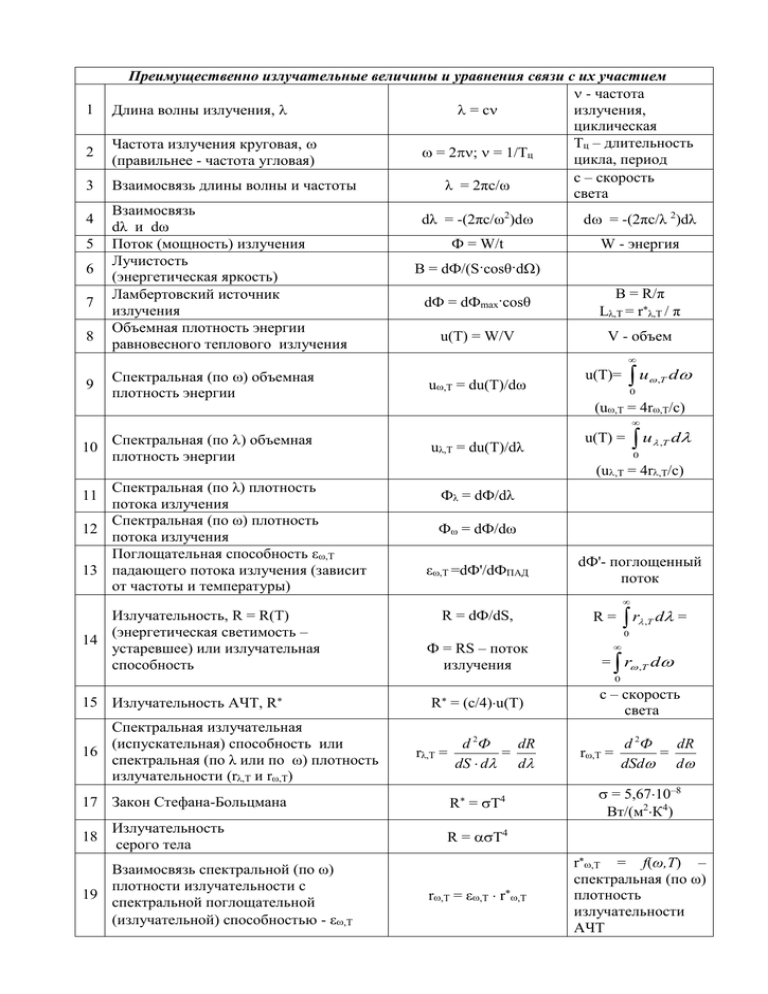
1 2 3 4 5 6 7 8 Преимущественно излучательные величины и уравнения связи с их участием - частота излучения, Длина волны излучения, = с циклическая Тц – длительность Частота излучения круговая, = 2; = 1/Тц цикла, период (правильнее - частота угловая) с – скорость Взаимосвязь длины волны и частоты λ = 2πс/ω света Взаимосвязь dλ = -(2πс/ω2)d d = -(2πс/λ 2)dλ dλ и dω Поток (мощность) излучения Ф = W/t W - энергия Лучистость B = dФ/(S·cosθ·dΩ) (энергетическая яркость) B = R/π Ламбертовский источник dФ = dФmax·cosθ излучения Lλ,T = rλ,T / π Объемная плотность энергии u(T) = W/V V - объем равновесного теплового излучения 9 Спектральная (по ) объемная плотность энергии u,T = du(T)/dω u u(T)= ,T d 0 (u,T = 4r,T/c) 10 Спектральная (по ) объемная плотность энергии uλ,T = du(T)/dλ u(T) = u ,T d 0 (u,T = 4r,T/c) Спектральная (по λ) плотность потока излучения Спектральная (по ω) плотность 12 потока излучения Поглощательная способность εω,Т 13 падающего потока излучения (зависит от частоты и температуры) 11 Фλ = dФ/dλ Фω = dФ/dω εω,Т =dФ'/dФПАД dФ'- поглощенный поток Излучательность, R = R(T) (энергетическая светимость – 14 устаревшее) или излучательная способность R = dФ/dS, r R= ,T d = 0 Ф = RS – поток излучения = r ,T d R = (c/4)u(T) с – скорость света 0 15 Излучательность АЧТ, R Спектральная излучательная (испускательная) способность или 16 спектральная (по λ или по ω) плотность излучательности (rλ,T и rω,T) 17 Закон Стефана-Больцмана 18 Излучательность серого тела Взаимосвязь спектральной (по ω) плотности излучательности с 19 спектральной поглощательной (излучательной) способностью - ε,T rλ,T = dR d 2Ф = dS d d R = T4 rω,T = dR d 2Ф = dSd d = 5,6710–8 Вт/(м2К4) R = T4 r,T = ε,T r,T r,T = f(ω,T) – спектральная (по ω) плотность излучательности АЧТ Взаимосвязь спектральной (по λ) плотности излучательности с 20 спектральной (по λ) поглощательной способностью - ελ,T rλ,T = ελ,T rλ,T Соотношение спектральных плотностей 21 излучательности по и по r,T = r,T d/d Закон Кирхгофа. 22 φ(λ,T) и f(ω,T) - универсальные функции Кирхгофа r ,T ,T r*,T ( , T ); 1 i r ,T r f ( , T ) 1 ,T i * ,T rλ,T = φ(λ,T) – спектральная (по λ) плотность излучательности АЧТ r,T = r,T 2c/2 = = r,T·(ω/λ) (r,T = ε,T r,T) (для АЧТ ε,T = 1) r,T = r,T = ω · f(/T); 3 23 Формулы Вина для малых частот излучения (больших длин волн) Формулы Релея - Джинса для больших 24 частот излучения (малых длин волн) 25 26 27 28 29 30 31 32 rλ,T = r,T 5 2 с f Т 2 = 2 2 kT ; 4 c rλ,T = 2πckT λ–4 Формула Планка (выражение через ω,T) r,T = f(ω,T) = 3 1 = 2 2 4 c exp 1 kT Формула Планка (выражение через λ,T) rλ,T = φ(λ,T) = 2hc 2 1 = 5 hc exp 1 kT Закон смещения (первый закон Вина) Второй закон Вина (для rmax,T) Функция F(/T) Функция (T) Энергия фотона Интегральная плотность энергии излучения фотонного газа 33 Давление фотонного газа 34 2 с 4 Теплоемкость фотонного газа при постоянном объеме h h exp kT 2 rλ,T = r,T · r,T = kT 2 (rλ,T = r,T · ) r,T = kT 1 = 2 h exp 1 kT rλ,T = kT 1 2 h exp 1 kT m = b1/T b1 = 2,89810–3 мК rmax,T = b2T5 b2 = 1,28710–5 Вт/(м3К5) F(/T) = r*,T/3 (T) = r*,T5 Eф = h 4 4 T u(T) = с 4 4 T p= 3с 16 3 T V CV = с 1 p u (T ) 3 d u (T ) V СV dT 35 Энтропия фотонного газа 36 37 38 39 40 41 S= 16 3 T V 3с Уравнение Эйнштейна для внешнего h = AB + EК фотоэффекта Уравнения де Бройля E = ; p k Момент импульса (момент количества L = mvr = Wt = nh движения). (Действие актуальное) ([Wt] = C = S) Действие потенциальное П = FS = Wl Импульс (количество движения) Pф = h/ Объемная плотность импульса P = P/V -23 Постоянная Больцмана k R / N A = 1.380658*10 Дж К-1 dS dU pdV T [П] = hc b1k P = mv = Ft







