Уроки повторения 11 класс по теме Функция

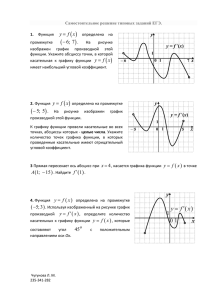
Уроки итогового повторения в 11 классе
Уроки итогового повторения имеют своей целью не только восстановление
в памяти учащихся основного материала, но и обобщение, уточнение и
систематизацию их знаний по алгебре и началам анализа за курс средней
школы.
Тематическое планирование уроков итогового повторения может быть
организовано разными путями по усмотрению учителя. Приведу один из
возможных вариантов планирования, в котором повторение учебного
материала объединено основными линиями курса алгебры и начал анализа. При
этом повторение начинается с обобщения знаний учащихся по теме «Функция»
(полученных ими в процессе изучения курса алгебры средней школы, где
функциональными отношениями завершалось формирование основных
понятий, и начал математического анализа). Повторение и закрепление свойств
основных элементарных функций будет продолжено при рассмотрении тем
«Уравнения и системы уравнений» и «Неравенства и системы неравенств».
Завершается обзорное повторение темой «Числа и алгебраические
преобразования». При этом учащиеся возвращаются к основным определениям
и понятиям курса алгебры. Поскольку элементарные функции и их свойства
уже повторены, то можно использовать тождественные преобразования для
упрощения выражений, уравнений и неравенств, содержащих эти функции, что
позволит закрепить знания учащихся по всем рассмотренным четырём темам.
При проведении уроков итогового повторения предполагается широкое
использование и комбинирование различных видов уроков (лекций, семинаров,
практикумов, медиауроков) с целью быстрого охвата большого по объёму
материала.
Необходимым элементом на уроках итогового повторения должна быть
самостоятельная работа учащихся. Она полезна как самим учащимся, так и
учителю для осуществления обратной связи. Задания для самостоятельной
работы должны быть иногда общими для всех учащихся класса (в двух
вариантах) и носить проверочный характер. А иногда дифференцироваться по
уровню трудности и быть индивидуальными.
Методика организации урока может быть самой разнообразной и
определяется учителем, исходя из специфики класса. Набор упражнений и
порядок их расположения позволяют в процессе решения этих задач повторить
и выстроить в систему основной теоретический материал урока.
Тема «Функция» (4 часа)
Н а п е р в о м (из двух) сдвоенных у р о к ов рассматриваются основные
понятия и свойства, связанные с функцией.
На предыдущем уроке учащиеся получили задание повторить, используя схемы
и алгоритмы справочника (у каждого ученика есть справочник по основным
вопросам курса «Алгебра и основы математического анализа»): общую схему
исследования функции и связанные с этой схемой свойства функции.
1. В ходе работы с тренажером «Чтение графиков функций»(слайды со 2 по 21)
повторяются следующие свойства функции: область определения,
множество значений, непрерывность (по графику), четность и нечетность,
геометрический смысл производной функции в точке, нули функции,
наибольшее и наименьшее значения, точки экстремума, экстремумы (диск с
тренажером прилагается)
№
слай
да
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
Задание
Ответ
Указать область определения функции
Указать множество значений функции
Указать область значений функции
Указать область определения функции
Указать множество значений функции
Указать наибольшее значение функции
Указать график чётной функции
Указать график нечётной функции
Найти значение производной в точке
Найти значение производной в точке
Найти значение производной в точке
Указать точку, в которой производная равна 0
2
3
4
2
2
2
4
3
4
1
1
2
Найти значение производной в точке
2
Указать, в какой точке значение производной
отрицательно.
Указать промежуток, которому принадлежит один
нуль функции
Указать промежуток, которому принадлежат два нуля
функции
Указать промежуток, которому принадлежат все нули
функции
Указать промежуток, которому принадлежит один
экстремум функции
Указать расстояние между точками экстремума
функции
[-5;5)
(-5;7)
(-2;6]
(-2;5]
[0;+∞)
4
4
3
Не существует
x=-1
=0
4
3
(-3;-1]
1
(1;4]
1
[-3;4]
1
[-2;2]
3
4
21.
Указать точку максимума
3
x=1
В ходе этой работы учащиеся, ответившие на 3-4 вопроса и подтвердившие
свои ответы знанием теоретического материала, получают отметки.
2. Основные функциональные умения могут быть продемонстрированы
учащимися при выполнении следующего задания:
Дана функция
, определённая на отрезке
. Исследуйте функцию.
Укажите:
множество значений функции;
координаты пересечения графика с осями координат;
промежутки знакопостоянства;
промежутки монотонности (промежутки убывания и возрастания);
точки, в которых производная равна нулю;
точки экстремума, вид экстремума, экстремумы;
точки, в которых функция принимает максимальное значение, чему оно
равно;
8. точки, в которых функция принимает минимальное значение. Чему оно
равно;
9. наибольшее и наименьшее значения функции на [ -2; 4 ];
10.является ли функция чётной или нечётной.
1.
2.
3.
4.
5.
6.
7.
Каждому ученику (в классе 17 человек) предоставляется схема
исследования функции и свой график функции. Выполненная работа
оценивается с выставлением отметок к следующему уроку (графики
функций прилагаются)
На в т о р о м у р о к е полезно отметить связь между постоянством
знака производной функции и её монотонностью на некотором
интервале, вспомнить алгоритмы решения задач на геометрический
смысл производной, на нахождение наибольшего (наименьшего)
значения функции на отрезке.
1. В ходе работы с тренажером «Чтение графиков функций» (слайды с 22
по 25) повторяются свойства функции, определяемые по заданному
графику её производной: монотонность функции, точки экстремума,
экстремумы.
№
слай
да
22.
Задание
Ответ
На рисунке изображен график производной функции у =f
(x),заданной на промежутке [-5;5]. Исследуйте функцию у =f
(x) на монотонность и укажите число промежутков убывания.
23. На рисунке изображен график производной функции у =f /(x),
заданной на промежутке [-5;5]. Исследуйте функцию у =f (x)
на монотонность и укажите число точек минимума .
24.
На рисунке изображен график производной функции у =f
/
(x),заданной на промежутке [-5;5]. Исследуйте функцию у =f
(x) на монотонность и укажите наибольшую точку максимума.
25.
Функция y = f(x) задана на промежутке (-5; 5).
График её производной y = f /(x) изображен на рисунке.
Определите значение х, в котором функция у = f(x) принимает
наименьшее значение на промежутке ( -5; 5).
/
2
3
2
3
2
3
1
2
2.С помощью диска «Виртуальный наставник , Алгебра, 10-11класс», в теме
«Применение производной» (диск прилагается) рассмотреть решение
следующих задач:
№1. Найти свободный член в уравнении касательной к графику функции
f(x )= 6x - x2 - 11 в точке х0 = -2
Уравнение касательной: y =
(x)= 6 - 2x;
x-
) ( y = kx +b)
= 10; y = 10x - 7;
Ответ: b= -7.
№2. Найти угловой коэффициент касательной, проведённой к графику
функции f(x)= 7 - 3x - 2x2 + 5x4 в точке с абсциссой x0= -2.
(x)= -3 - 4x + 20x3
(x0)= -155.
Ответ: k= -155.
№3. Найти сумму координат точки на графике функции f(x)=5x2 - 9x + 3,
обладающую тем свойством, что угол между касательной, проведённой к
графику в этой точке, и положительным направлением оси абсцисс равен
450.
(x)= 10x – 9;
10x0 – 9 = 1;
x0= 1;
y0 = -1.
Ответ: x0 + y0= 0
№4. Найти координаты точки на графике функции
f(x) = e4x + 3, если
касательная, проведённая к графику функции в этой точке, параллельна
прямой y = 4x + 6.
(x) =4e4x;
(
4
)=4
=4
=1
4
=0
= 0; y0 = 4
Ответ: (0; 4)
№6. Функция y = f(x) определена на промежутке (-6; 5). На рисунке
изображён график её производной. Найти длину промежутка убывания
этой функции.
(x)  0 при x (2; -2)
y = f(x) убывает.
Длина промежутка равна
= 4.
Ответ: 4
№7. Найти наибольшее значение функции f(x) =
1)
(x =
2)
(x) = 0;
=
x2 = 4; x = ± 2
3) x1 = 2 [0; 2]; x2 = -2
4) f ( 2 ) = 1; f( 0 ) = 0
Ответ:
на отрезке [0; 2]
[0; 2]
max f(x) = f(2) = 1
[0; 2]
№8. При каком наименьшем целом положительном значении функция
f (x ) = x 2
x
+
x
+ 5 возрастает на всей области определения?
(x)  0
+ x2
(x) = 2x
+
(x)  0
(2x + x2 +
x2 + 2x +
)0
0
2x2 + 4x + a2  0
= 4 – 2a2
4 – 2a2  0
2a2  4
a2  2
a (- ; -
) (
;
)
a z; a  0  a = 2
Ответ: a = 2.
№9. При каком значении параметра а функция f (x) = log2 (ax2 + 2x+ 3)
имеет в точке х0 = -2 минимум?
(
) = 0;
(x) =
;
(-2) = 0;
=0


 a = 0,5
№10. Число 72 представим в виде суммы двух слагаемых так, что
сумма их квадратов наименьшая. Найти меньшее число.
х – первое число; (72 – х) – второе число;
(x) = 4x – 144;
f (x);
(x) = 0; x = 36;
Ответ: 36
Задачи № 1, № 4, № 7, №10 решаются всеми учащимися при коллективном
обсуждении, задачи № 2, № 3, № 6 можно предложить для самостоятельного
решения с последующей проверкой, задачи № 8,№ 9 решаются всеми
учащимися при коллективном обсуждении с просмотром решения со звуковым
сопровождением.
Домашнее задание задаётся по сборнику «Математика ЕГЭ-2009,тематические
тесты, 10-11 класс, часть II (B4-B8,C1-C2) под редакцией Ф.Ф.Лысенко (у
каждого ученика 2 таких сборника, часть I –A1-A10,B1-B3 и часть II) в
сборниках по 10 вариантов. Варианты закреплены за учащимися с 10 класса
следующим образом: 1-3 варианты -для менее подготовленных учащихся, 4-7
варианты – для учащихся с более высоким уровнем притязаний, 8-10 – для
учащихся, обучающихся только на «4» и «5».
Д/з.1). 5, B5, Геометрический смысл производной.(часть II, с.37)
2). Повторить по справочнику схему исследования функции с
помощью производной.
В вариантах по 8 заданий. Выставляются отметки за верно выполненные:
7-8 заданий – «отлично
5-6 заданий – «хорошо»
1-4 – «удовлетворительно»
На следующих двух уроках нужно: 1).выполнить исследование заданной
функции с помощью производной и построить её график; 2).рассмотреть
первообразные данных функций и геометрический смысл интеграла.
Для работы над этим материалом можно использовать:
1).диск «Виртуальный наставник, Алгебра, 10-11класс», в теме «Интеграл»;
2). медиатеку цифровых ресурсов по всем темам курса «Алгебра и начала
анализа, 10-11 класс», созданной с помощью Единой коллекции цифровых
образовательных ресурсов(school-collection.edu.ru), например:
 папка «Производная», файл №72 «Полная схема исследования функции”,
файл №73 «Исследование дробно-рациональной функции”;
 папка «Интеграл», файл №13 «Решение задач по теме «Площадь
криволинейной трапеции», файл №17 «Вычисление площади с помощью
интеграла» и другие.