МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

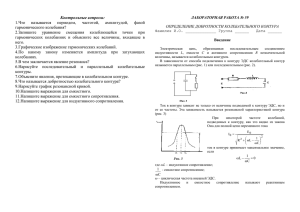
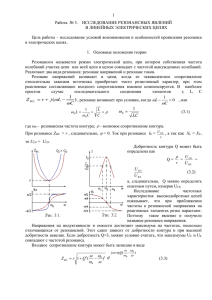
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
«МОСКОВСКИЙ АВИАЦИОННЫЙ ИНСТИТУТ
(национальный исследовательский университет)» (МАИ)
ФИЛИАЛ «ВЗЛЕТ»
кафедра РЭВС ЛА
Нестеров С. В.
ИССЛЕДОВАНИЕ ИЗБИРАТЕЛЬНЫХ СВОЙСТВ
КОЛЕБАТЕЛЬНЫХ КОНТУРОВ
Методическое указание к лабораторным работам по дисциплине
«ОСНОВЫ ТЕОРИИ ЦЕПЕЙ»
Ахтубинск - 2015
ОПИСАНИЕ ЛАБОРАТОРНОЙ УСТАНОВКИ
Исследование избирательных свойств колебательных контуров производится на установке, блок-схема которой указана на рис 0.1.
Рис.0.1 Блок-схема лабораторной установки.
Лабораторная установка состоит из задающего генератора (ГНЧ Г3112), макета, милливольтметра (МВ В3-38В), милливольтметра (МВ В338Б) и магазина сопротивлений (МС).
Задающий генератор (ГНЧ Г3-112) является источником синусоидального напряжения или напряжения прямоугольной формы в зависимости от положения ключа на макете. С выхода генератора сигнал заданной
амплитуды и частоты подается на вход макета.
Лабораторный макет содержит магазины индуктивностей, ёмкостей и
резисторов. Для расширения возможностей к макету подключается внешний магазин сопротивлений (МС). Макет предназначен для сборки исследуемой электрической цепи. Сборка цепи, состоящей из сопротивлений
Z1, Z2, Z3, R, производится с помощью переключателей.
Милливольтметр (МВ В3-38В) предназначен для измерения действующих напряжений на входе и на пассивных элементах исследуемой цепи.
Подключение вольтметра к тому или иному участку цепи производится с
помощью переключателей, установленных на макете.
Милливольтметр (МВ В3-38Б) подключён к задающему генератору
(ГНЧ Г3-112) и предназначен для контроля заданного уровня входного
напряжения.
1. ИССЛЕДОВАНИЕ ЧАСТОТНЫХ ХАРАКТЕРИСТИК ПОСЛЕДОВАТЕЛЬНОГО КОЛЕБАТЕЛЬНОГО КОНТУРА.
Цель работы – исследовать амплитудно-частотные и фазо-частотные
характеристики последовательного контура (рис 1.1).
Рис.1.1 Исследуемая схема с последовательным колебательным контуром.
Основные понятия, расчётные формулы и определения
Амплитудно-частотной характеристикой (АЧХ) цепи называется
частотная зависимость отношения амплитуды гармонического выходного
сигнала к амплитуде гармонического входного сигнала.
Фазочастотной характеристикой (ФЧХ) называется частотная зависимость разности начальных фаз гармонических выходного и входного
сигналов.
В электрических цепях, содержащих индуктивные и емкостные элементы, амплитуда тока может резко изменяться, когда частота внешнего
воздействия достигает некоторого определённого значения. Это явление
называется амплитудным резонансом. В теории цепей под резонансом
понимают фазовый резонанс – такой режим работы электрической цепи,
при котором реактивная составляющая выходного сигнала равна нулю.
Это получается, когда реактивные оставляющие входного сопротивления
и проводимости равны нулю. Простейшей цепью, в которой наблюдается
явление резонанса, является одиночный колебательный контур, представляющий собой цепь, состоящую из конденсатора С и индуктивной катушки L, соединённых последовательно или параллельно.
Последовательный колебательный контур (рис.1.1) представляет
собой цепь, содержащую индуктивную катушку L с потерями r, конденсатор C и резистор R, соединённые последовательно с источником сигнала.
При сопротивлении катушки r, много меньшем сопротивления резистора
R, схема имеет вид, показанный ниже (рис.1.2).
Рис.1.2 Схема с последовательным колебательным контуром при r<<R.
Комплексное входное сопротивление контура
Z(j) = R + jx() = R + j(L – 1/C),
где R - активное сопротивление контура
x() = xL() + xC() = L – 1/C – реактивное сопротивление контура, определяется индуктивностью катушки L и ёмкостью конденсатора C.
 - угловая частота, связанная с циклической частотой f соотношением
Мнимая часть сопротивления зависит от частоты и на определенной
частоте ω0 она может обратиться в ноль
Решая это уравнение, можно определить частоту
, которую назы-
вают резонансной
.
Она определяется параметрами элементов контура L, C.
Модуль входного сопротивления контура (рис.1.3а) минимален на
резонансной частоте.
Ток в контуре на этой частоте достигнет максимальной величины,
которая зависит только от сопротивления нагрузки R и не зависит от сопротивления контура
В радиотехнике такой электрический режим в колебательном контуре называют фазовым резонансом. Это название связано с тем, что разность фаз между током и входным напряжением (рис.1.3б) на резонансной
частоте
равна нулю, а на произвольной частоте определяется выраже-
нием
а)
б)
Рис.1.3 Зависимость сопротивления контура (а) и угла сдвига фаз
(б) от частоты.
Таким образом, условием резонанса в колебательном контуре является x(ω0) = 0.
Резонанс возникнет в том случае, если частота входного сигнала будет равна резонансной частоте контура ω = ω0. .
На резонансной частоте модуль сопротивления емкости равно модулю
сопротивления индуктивности
Эта величина
называется характеристическим или волновым сопротивлением контура.
В реальных контурах оно имеет значение от сотен Ом до десятков
кОм.
Напряжения на реактивных элементах L,C на резонансной частоте
определяется
= jI0ω0L= jI0ρ = j
= jQ
;
=
=Q
;
где
= -jI0ρ = -j
=
=Q
=
= -jQ
;
;
- добротность контура, которая показывает, во сколько раз
амплитуда напряжения на реактивных элементах контура на ω 0 превышает амплитуду напряжения источника питания U1.
Таким образом, напряжение на реактивных элементах в Q раз больше
входного напряжения и равны между собой по модулю, но противоположны по знаку, поэтому резонанс в последовательном колебательном
контуре называют резонансом напряжений.
Значение тока в контуре в зависимости от частоты выражается формулой
,
где Z = R
- модуль комплексного сопротивления,
– расстройка контура.
Коэффициенты передачи напряжений на реактивных элементах контура определяются выражениями:
- коэффициент передачи напряжения на
индуктивности,
– коэффициент передачи напряжения на
ёмкости.
Резонансные характеристики коэффициентов передачи напряжений
на элементах контура приведены на рис.1.4.
Рис.1.4 Зависимость коэффициентов передачи напряжений на реактивных элементах от частоты.
Частоты, на которых напряжения на индуктивности и ёмкости становятся максимальными, зависят от добротности:
,
где d =
,
- затухание контура.
На резонансной частоте в последовательном колебательном контуре
возникает непрерывный процесс колебания энергии между индуктивностью и емкостью без участия внешнего источника энергии.
Энергия электрического поля емкости переходит в энергию магнитного поля индуктивности и наоборот. Поэтому цепь RLC называют последовательным колебательным контуром.
Важнейшей особенностью колебательного контура является способность выделять на резисторе R из суммы гармонических колебаний различных частот входного сигнала только те колебания, частота которых лежит
вблизи резонансной частоты. Это свойство называется избирательностью
цепи.
Принято считать, что контур пропускает сигналы в определенном
диапазоне частот, называемом полосой пропускания. В идеальном случае
выходной сигнал избирательной цепи в пределах полосы пропускания
должен иметь постоянное значение и быть равным нулю за пределами полосы пропускания (рис.1.5, кривая 1).
Амплитудно-частотная характеристика (АЧХ) последовательного колебательного контура определяется выражением
.
АЧХ реальных избирательных цепей (кривая
Кi
2 на рис.1.5) отличаются от прямоугольной фор1
1 ==
2
мы отсутствием резкой границы между диапазоωω
0,7
()
ном пропускаемых и подавляемых частот.
07
Полоса пропускания реальных избиратель ных цепей определяется как диапазон частот S =
  В
В - Н, в пределах которого ток в контуре
н
0
Рис.1.5. Нормированные
АЧХ
н
уменьшается до уровня 1/√2 = 0,707 от максин.
идеальной
–
1;
реальной
–
2
цепи
мальногоρзначения (рис.1.5).
нн
Избирательные
свойства контура определяются формой АЧХ, в частнн
ности, крутизной
склонов АЧХ. Чем ближе она к прямоугольной форме,
нн
нн
тем вышен избирательность (рис.1.5).
Количественно
избирательность можно оценить коэффициентом
Н
прямоугольности
Кп =
,
где S0,1 – полоса пропускания на уровне 0,1 от максимального значении
S0,7 – полоса пропускания на уровне 0,7 от максимального значения
На границах полосы пропускания модуль коэффициента передачи тока колебательного контура K(в,н) = 0,707Ki(0).
Мощность выходного сигнала на границах полосы пропускания составляет половину мощности при резонансе
.
Полоса пропускания контура находится из соотношения:
.
Отсюда верхняя и нижняя границы полосы пропускания:
;
.
Ширина полосы пропускания определяется как разность этих частот и
зависит от параметров контура 0 и Q , и не зависит от емкости C :
.
Чем больше Q, тем уже полоса пропускания.
ДОМАШНЕЕ ЗАДАНИЕ
1. По конспекту лекций или учебнику по курсу ОТЦ, ознакомиться с
основами теории последовательного контура.
2. Нарисовать схему последовательного колебательного контура, содержащую катушку индуктивности с параметрами L,r , ёмкость C и резистор R. Вычислить его резонансную частоту f0, характеристическое сопротивление ρ, сопротивление нагрузки R исходя из заданной добротности Q,
полное активное сопротивление контура R0 по формулам
;
;
;
→
;
.
Параметры элементов контура по вариантам приведены в табл.1.1
ТАБЛИЦА 1.1
вариант
1
2
3
4
C, мкФ
0,05
0,02
0,02
0,25
L, мГн
30
40
40
10
r, Ом
86
110
80
32
Q
3,5
3,37
2,35
1,51
3. Рассчитать частоты, на которых коэффициенты передачи напряжения на катушке индуктивности и ёмкости будут максимальны:
,
,
,
,
где νL ,νC – приведённые частоты.
4. Рассчитать нижнюю и верхнюю границы полосы пропускания, ширину полосы пропускания:
;
,
;
,
.
5. Рассчитать частоты, на которых произведутся измерения напряжений на катушке индуктивности, ёмкости
f=(0,25; 0,5;νн; νс; 1; νL; νв; 1,5; 2; 2,5; 3; 5)f0.
ПОРЯДОК ПРОВЕДЕНИЯ РАБОТЫ
1. Собрать последовательный колебательный контур, для чего к зажимам 1-2 (рис 0.1) подключить катушку индуктивности L,r, к зажимам 2-3 –
конденсатор C, а к зажимам 3-4 - нагрузку R. Зажимы 2-4 оставить свободными от пассивных элементов.
2. С выхода генератора на вход цепи подать сигнал частотой f=0,25f0 и
напряжением U1=5 В, для чего ручкой «рег.вых» генератора добиться показания милливольтметра В3-38Б 5 В.
3. Измерить напряжение на катушке индуктивности, ёмкости, резисторе, т.е поочерёдно подключать милливольтметр В3-38В с помощью переключателей к зажимам 1-2, 2-3, 3-4. Результаты измерений занести в
таблицу 1.2.
4. Продолжить измерения на остальных частотах f, рассчитанных в п.5
домашнего задания, поддерживая входное напряжение U1=5 В.
f,кГц
ТАБЛИЦА 1.2
ν=
Измеренные величины
UL
В
UC
В
U2
В
Вычисленные величины
мА
Ом
0,25
0,5
….
5
I0 – ток на резонансной частоте f0, выбирается из таблицы
5.Обработка результатов измерений. Обработка сводится к выполнению операций, указанных в колонках таблицы 1.2.
6. По результатам измерений построить зависимости Z(f), Кi(f)= ,
,
. Показать на графиках граничные частоты fн, fв.
7. Определить по характеристикам полосу пропускания S0,7 на уровне
0,707Кimax, рассчитать добротность Q.
8. Определить полосу пропускания S0,1 на уровне 0,1Кimax .
9. Оценить избирательность контура по коэффициенту прямоугольности
Кп =
.
Указания к оформлению отчёта
Отчёт должен содержать:
1) Результаты выполнения домашнего задания;
2) Принципиальную схему исследуемой цепи;
3) Результаты измерений, сведённые в таблицу 1.2;
4) Графики частотных характеристик, выполненные на миллиметровке;
5) Выводы и оценку полученных результатов.
Вопросы для самопроверки
1. Дать определение явления резонанса в электрической цепи, запишите
условия возникновения резонанса.
2. Запишите параметры последовательного колебательного контура (f0,
Q, S, Z(f0), ρ, d, ε).
3. Как влияют R, L, C на параметры контура.
4. Как производится расчёт коэффициентов передачи по напряжению последовательного контура? Объясните форму характеристик в области
нижних, средних и верхних частот относительно f0. Показать на графике, как изменяются частотные характеристики при изменении R, L,
C.
5. Как определить параметры контура f0, fн, fв, S, Кп по частотным характеристикам?
6. Определить активную мощность контура на границах полосы пропускания и при резонансе.
2. ИССЛЕДОВАНИЕ ЧАСТОТНЫХ ХАРАКТЕРИСТИК ПАРАЛЛЕЛЬНОГО КОЛЕБАТЕЛЬНОГО КОНТУРА
Цель работы – исследовать амплитудно-частотные и фазо-частотные
характеристики параллельного контура (рис.2.1).
Рис.2.1 Исследуемая схема с параллельным колебательным контуром.
Основные понятия, расчётные формулы и определения
Параллельный колебательный контур – это цепь, составленная из
конденсатора и катушки индуктивности, соединённых параллельно.
Существует несколько схем параллельного колебательного контура:
Рис.2.2 Схемы параллельного колебательного контура.
В данной лабораторной работе рассмотрим параллельный колебательный фильтр 1 вида, используемый как заграждающий или полосовой
фильтр, т.е фильтр который не пропускает в нагрузку сигналы определенной частоты, а остальные сигналы пропускаются без существенного
ослабления.
Комплексная проводимость участка цепи ав
.
Для возникновения резонанса по определению необходимо чтобы
реактивная составляющая контура была равна нулю
.
Следовательно, резонанс можно вызвать в данной цепи либо путём
изменения rLC элементов, либо изменяя ω.
Значит резонанс наступит на частоте
,
где
- волновое сопротивление контура;
- резонансная частота при последовательном обходе
контура (резонансная частота идеального параллельного колебательного
контура, совпадает с резонансной частотой последовательного колебательного контура).
Из данной формулы видно:
1) Что резонансная частота контура с потерями r, меньше резонансной частоты идеального колебательного контура без потерь.
2) Если сопротивление потерь r равно волновому сопротивлению ρ,
резонанс токов возникает на частоте близкой к нулю.
3) Если сопротивление потерь r больше волнового сопротивления ρ,
то резонанс токов не возможен.
Сопротивление потерь в реальных радиотехнических контурах
обычно мало по сравнению с индуктивным сопротивлением r << ωL. Поэтому сопротивление вблизи резонанса можно определить по формуле
,
где
– расстройка контура,
- добротность контура при последовательном обходе.
При резонансе, когда расстройка контура равно нулю, сопротивление
носит чисто активный характер и выражается формулой
Zав (ω=ω0) = Q1ρ .
Полное сопротивление рассматриваемой цепи равно сумме сопротивлений
,
где
,
– добротность параллельного колебательного контура,
φ = arctg βε – arctg Q1ε – сдвиг фаз между током неразветвлённой части цепи и входным напряжением
Модуль входного сопротивления имеет максимум на резонансной
частоте, т.к проводимость контура минимальна на резонансной частоте
(рис.2.3, а).
Угол φ положителен при индуктивном характере цепи (на частотах
меньше резонансной), при этом ток отстаёт по фазе от входного напряжения, и отрицателен при ёмкостном характере цепи (на частотах больше
резонансной), когда ток опережает по фазе входное напряжение. На резонансной частоте сдвиг фаз равен нулю, т.к цепь при этом носит активный
характер (рис.2.3, б).
Комплексное действующее значение тока неразветвлённой части цепи определяют по закону Ома
,
где
- значение тока при резонансе.
Комплексное действующее значение напряжения на участке ав
.
а)
б)
Рис.2.3 Зависимость сопротивление контура (а) и угла сдвига фаз (б) от
частоты.
Комплексные коэффициенты передачи напряжения на участке ав и
на нагрузке:
;
.
Комплексные действующие значения токов в ветвях контура
,
.
Токи через реактивные элементы на резонансной частоте в Q1 раз
превышают ток через неразветвлённый участок цепи. По фазе токи противоположны. Резонанс в параллельном контуре называют резонансом токов.
.
Зависимость токов протекающих в ветвях контура от приведённой частоты и зависимость коэффициентов передачи напряжений от приведённой
частоты представлены на рис.2.4 и рис.2.5
Рис.2.4 Зависимость токов протекающих в ветвях контура от приведённой частоты.
Рис.2.5 Зависимость коэффициентов передачи напряжений от приведённой частоты.
Из графиков видно, что напряжение на нагрузке при резонансе достигает своего минимума. Это означает, что рассматриваемая цепь как и
последовательный колебательный контур обладает избирательностью.
Полоса задерживания – это полоса частот в пределах которой коэффициент передачи напряжения на резисторе R меньше, чем
. Цепь,
обладающая такими свойствами, называется заграждающим фильтром.
Коэффициент передачи напряжения на контуре имеет максимум на
резонансной частоте, на которой
меньше или равно 1. В этом случае
(при снятии напряжения с контура) данную цепь можно рассматривать
как полосовой фильтр, который в полосе пропускания имеет коэффициент передачи напряжения больше, чем
.
Энергетические процессы в цепи при резонансе токов аналогичны
процессам, происходящим при резонансе напряжений.
Реактивная энергия действует внутри контура: в одну часть периода
энергия магнитного поля индуктивности переходит в энергию электрического поля емкости, в следующую часть периода энергия электрического
поля емкости переходит в энергию магнитного поля индуктивности. Обмена реактивной энергией между потребителями цепи и источником
напряжения при резонансе не происходит.
ДОМАШНЕЕ ЗАДАНИЕ
1. По конспекту лекций или учебнику по курсу ОТЦ, ознакомиться с
основами теории параллельного контура.
2. Нарисовать схему параллельного колебательного контура, содержащую катушку индуктивности с параметрами L,r , ёмкость C и резистор R.
Вычислить его резонансную частоту f0, характеристическое сопротивление ρ, добротность контура Q1, Q2 по формулам
;
;
;
;
.
Параметры элементов контура по вариантам приведены в табл.2.1
вариант
1
2
3
4
C, мкФ
0,1
0,1
0,25
0,25
L, мГн
40
50
30
30
ТАБЛИЦА 2.1
R, Ом
870
625
610
534
r, Ом
80
148
60
90
3. Рассчитать частоты, на которых произведутся измерения напряжений на участке ав и нагрузке
f=(0,25; 0,5; 0,75; 1; 1,5; 2; 2,5; 3; 3,5; 4; 4,5; 5)f0 .
4. Рассчитать сопротивление участка цепи Zав и полное сопротивление
цепи Z при резонансе
Zав = Q1ρ ;
Z = R + Zав .
5. Рассчитать ток неразветвлённой части цепи, напряжение участка цепи ав и токи в ветвях при резонансе
;
;
;
.
6. Рассчитать коэффициенты передачи напряжения на участке ав и на
нагрузке при резонансе
;
.
ПОРЯДОК ПРОВЕДЕНИЯ РАБОТЫ
1. Собрать параллельный колебательный контур, для чего к зажимам 12 (рис 0.1) подключить катушку индуктивности L,r, и конденсатор C, а к
зажимам 2-4-сопротивление нагрузки R. Зажимы 2-3 и 3-4 оставить свободными от пассивных элементов.
2. С выхода генератора на вход цепи подать сигнал частотой f=0,25f0 и
напряжением U1=5 В, для чего ручкой «рег.вых» генератора добиться показания милливольтметра В3-38Б 5 В.
3. Измерить напряжение на участке цепи ав и резисторе, т.е поочерёдно подключать милливольтметр В3-38В с помощью переключателей к зажимам 1-2, 2-4. Результаты измерений занести в таблицу 2.2
4. Продолжить измерения на остальных частотах, поддерживая входное
напряжение U1=5 В.
5. Обработка результатов измерений. Обработка сводится к выполнению арифметических операций, указанных в колонках таблицы 2.2 и
определения угла сдвига фаз между входным напряжением и током в цепи
(выходным напряжением) путём построения векторных диаграмм.
ТАБЛИЦА 2.2
Измеренные величины
Uав
В
Вычисленные величины
U2
В
мА
мА
мА
Ом
0,25
0,5
…
5
6. По
результатам
,
измерений построить зависимости Z(f), φ(f),
,
,
(I0 – ток на резонанс-
ной частоте, выбирается из таблицы 2.2)
7. Определить по характеристикам полосу пропускания S0,7 по уровню
0,707Кав мах , рассчитать добротность Q , показать на графиках нижнюю fн
и верхнюю fв границы полосы пропускания.
φ,г
f,кГц
ν=
8. Определить по характеристикам полосу пропускания S0,1 по уровню
0,1Кав мах.
9. Оценить избирательность контура по коэффициенту прямоугольности
.
10. Определить по характеристикам полосу задерживания, показать на
графиках границы полосы задерживания.
Указания к оформлению отчёта
Отчёт должен содержать:
1) Результаты выполнения домашнего задания;
2) Принципиальную схему исследуемой цепи;
3) Результаты измерений, сведённые в таблицу 2.2;
4) Графики частотных характеристик, выполненные на миллиметровке;
5) Выводы и оценку полученных результатов.
Вопросы для самопроверки
1. Дать определение явления резонанса в электрической цепи, запишите
условие возникновения резонанса в параллельном колебательном контуре 1 вида.
2. Как отличается резонансная частота идеального колебательного контура от резонансной частоты контура 1 вида?
3. Запишите параметры параллельного колебательного контура (f0, Q, S,
Z(f0), ρ, d, ε).
4. Как влияют R, L, C на параметры контура.
5. Объясните форму характеристик в области нижних, средних и верхних
частот относительно f0. Показать на графике, как изменяются частотные характеристики при изменении R, L, C.
6. Как определить параметры контура f0, fн, fв, S, Кп по частотным характеристикам?
7. Определить активную мощность, потребляемую контуром на резонансной частоте.
8. В каких случаях исследуемую цепь можно применять в качестве заграждающего фильтра, а в каких в качестве полосового фильтра?
9. Во сколько раз при резонансе ток через индуктивность и ёмкость превышают ток неразветвлённой части цепи?
1.
2.
3.
4.
5.
6.
7.
ЛИТЕРАТУРА
Атабеков Г.И. Основы теории цепей. Учебник для вузов. М., «Энергия»,
1969. 424 с.
Г.В. Зевеке, П.А. Ионкин, А.В. Нетушил, С.В. Страхов. Основы теории
цепей. Учебник для вузов. Изд. 4-е переработанное. М., «Энергия», 1975.
752 с.
Улахович Д.А. Основы теории линейных электрических цепей: Учеб.
Пособие. – СПб.:БХВ-Петербург,2009.-816 с.:Учебная литература для
вузов.
Бессонов Л.А. Теоретические основы электротехники: Электрические
цепи: Учебник для электротехн., энерг., приборостроит. спец. вузов.-8-е
изд., перераб. и доп.-М.: Высш. шк., 1984.-559 с.
Добротворский И.Н. Теория электрических цепей: Учебник для техникумов. - М.: Радио и связь, 1989.-472с.
Нейман Л.Р., Демирчян К.С. Теоретические основы электротехники: В
2-х т. Учебник для вузов. Том 1.-3-е изд., перераб. и доп. - Л.: Энергоиздат. Ленингр. отд-ние, 1981.-536с.
М.Р. Шебес, М.В. Каблукова. Задачник по теории линейных электрических цепей: Учеб. пособ. для электротехнич., радиотехнич., спец вузов.4-е изд., перераб. и доп.-М.: Высш.шк., 1990.-544с.