Конспект урока

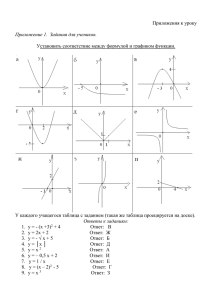
Конспект урока
Тема урока: Способы задания функции
Класс: 9;
Цели урока:
Образовательная: рассмотреть способы задания функции: аналитический, графический, табличный, словесный;
закрепить эти понятия в ходе выполнения упражнений; показать учащимся, что понятия не изолированы друг от друга, а
представляют собой определенную систему, все звенья которой находятся во взаимной связи; формирование умения
анализировать, обобщать, классифицировать.
Воспитательная: формирование качеств личности: самостоятельности, ответственности за принятые решения,
культуры общения.
Развивающая: развивать мыслительную деятельность школьников, математическую речь, память.
Тип урока: урок формирования новых знаний;
Литература: Мордкович, А.Г. Алгебра. 9кл.: В двух частях. Ч.1: Учебник для общеобразовательных учреждений/А.Г.
Мордкович.-6-е изд.-М.: Мнемозина, 2004.-192 с.: ил.
Мордкович, А.Г. Алгебра. 9кл.: В двух частях. Ч.2: Задачник для общеобразовательных учреждений/А.Г. Мордкович,
Т.Н. Мишустина, Е.Е. Тульчинская.-8-е изд., исп.-М.: Мнемозина, 2006.-152с.:ил.
Занина, О.В., Данкова, И.Н. Поурочные разработки по алгебре к учебному комплекту А.Г. Мордковича: 9 класс.- М.:
ВАКО,2007.-496с.- (В помощь школьному учителю).
План.
1.
2.
3.
4.
5.
6.
Организационный момент(1мин.)
Этап постановки цели урока(1 мин.)
Введение новых знаний(25 мин.)
Решение задач(10 мин.)
Подведение итогов урока(5 мин.)
Задание на дом(2 мин.)
Ход урока
Деятельность учителя
I. Учитель отмечает отсутствующих, проверяет
наличие тетрадей.
II. На прошлых уроках мы уже познакомились с
числовыми функциями, областью определения и
областью значений. А сегодня мы познакомимся со
способами задания функции.
III. В первой половине XVII в. В связи с развитием
механики в математику проникают идеи изменения и
движения. В это время начинает складываться
представление о функции как о зависимости одной
переменной величины от другой.
Французский математик Пьер Ферма (1601-1665) и
Рене Декарт (1596-1650) представляли себе функцию
как зависимость ординаты точки кривой от ее
абсциссы.
Английский ученый Исаак Ньютон (1642-1727)
понимал функцию как изменяющуюся в зависимости
Деятельность учащихся
Методы Формы
Рассказ
Фронтальная
от времени координату движущейся точки.
Термин «функция» ( от английского functioисполнение , совершение) впервые ввел немецкий
математик Готфрид Лейбниц (1646-1716) и член
Петербургской Академии знаменитый математик
XVIII в. Леонард Эйлер (1707-1783) рассматривали
функцию как аналитическое выражение.
Функцию как зависимость одной переменной
величины от другой ввел чешский математик
Бернард Больцано (1791-1848).
Что называется функцией?
Что значит задать функцию?
Задать функцию – значит указать правило, которое
позволяет по произвольно выбранному значению х из
D(f) вычислить соответствующее значение у. чаще
всего это правило связано с формулой или
Функция- это «закон», по которому
Опрос
каждому элементу одного множества
(называемому областью определения)
ставится в соответствие некоторый
элемент другого множества
(называемого областью значений).
Если даны числовое множество Х и
правило f, позволяющее поставить в
соответствие каждому элементу х из
множества Х определенное число у,
то говорят, что задана функция y=f(x)
с областью определения Х.
Индивидуальная
Фронтальная
рассказ
несколькими формулами – такой способ задания
функции обычно называют аналитическим. Ранее вы
рассматривали только такой способ задания
функции, но существуют и другие.
Пусть F – некоторая линия на координатной
плоскости и пусть спроецировав эту линию на ось
ОХ, мы получим [a,b]. Возьмем произвольную точку
х из [a,b] и проведем через нее прямую,
параллельную оси ординат. Потребуем
дополнительно , чтобы каждая такая прямая
пересекала линию F только в одной точке. При
пересечении мы получили точку, ордината которой –
это число f(x), соответствующее выбранному
значению х. Тем самым на [a,b] задана функция f(x).
Такой способ задания функции называется
графическим, а линия F- график функции.
Если функция была аналитической и нам удалось
построить график функции, то мы фактически
перешли от аналитического способа задания функции
к графическому. Обратный переход осуществим не
всегда.
Не всякая линия на координатной плоскости может
рассматриваться как график некоторой функции.
Например, окружность, заданная уравнением х2+у2=9
не является графиком функции, поскольку любая
прямая х=а, где |a|<3, пересекает эту линию в двух
точках. В то же время эту окружность можно
разрезать на две части- верхнюю полуокружность и
нижнюю- то каждую из полуокружностей можно
считать графиком некоторой функции, причем в
обоих случаях несложно от графического способа
задания функции перейти к аналитическому.
Кроме аналитического и графического , на практике
применяют табличный способ задания функции. При
этом способе приводится таблица, в которой указаны
значения функции для конечного множества
значений аргумента. Например, квадратов чисел,
кубов чисел, квадратных корней и т.д.
Также в математике используют словесный способ,
когда правило задания функции описывается
словами.
IV. Решение задач на готовых чертежах.
Является ли графиком какой-либо функции фигура,
изображенная на рисунках? Если да, то задайте ее
аналитически.
Учащиеся по цепочке отвечают
является ли графическим заданием
какой – либо функции, изображенная
на рисунках.
А) является;
Б) не является;
В) является;
Г) не является;
Д) является;
А) не является;
Б) не является;
В) является у=х+2;
Г) является у=2|х|-2;
Д) не является;
Устный
опрос
Индивидуальная
Е) является
2, при х<-2;
У= -x, при -2<x<2;
-2, при х>2.
Задайте аналитически функции, графики которых
изображены на рисунках 25-36, если это возможно.
25) у=х2;
26) не является графиком функции;
27) у = √х + 4;
28) у=(х+2)2+4
29) у=-х+1
30) у=(х+2)2-2
31) у=1,5х+2
32) у=(х-2)2+4
33) у=2/х
34) у = −√х + 5 + 2
35) у = √х + 2 − 1
36) у=-3/х
№ 9.7 Функция задана формулой s=90t, где s – путь
(в км) и t – время (в ч) найдите s(1), s(2,5), s(4)
В данной задаче в качестве аргумента
выступает t, а значения функции-s.
Значит s(1)=90*1=90;
S(2,5)=90*2,5=225;
S(4)=90*4=360.
Найдите t, если s=1800 км
t=s/90
t=1800/90
t=20
Найдите s, если t=15мин.
15 мин=0,25 ч.
S=0,25*90=22,5.
Найдите t (в мин), если s=450 м.
t=s/90
t=0,45/90
t=0,005(ч)=0,005*60=0,3(мин)
№9.8 Функция задана формулой t=s/12, где s – путь
(в км) и t – время (в ч) найдите t(36),t(2,7),t(144)
t(36)= 36/12=3(ч);
t(2,7)= 2,7/12=0,225(ч)
t(144)=144/12=12(ч)
Найдите s, если t=4,5 ч.
s=12t=12*4,5=54(км)
Найдите t, если s=150м.
t=s/12=0,15/12=0,0125(ч)
Найдите s(в м), если t=45с.
V. какие способы задания функции вы знаете?
Как определить, является ли графическим заданием
какой – либо функции изображенная фигура?
VI. п. 8 № 8.30, 9.11.
t=1/80(ч)
s=12t=12*1/80=3/20(км)=3/20000(м)
Аналитический, графический,
табличный, словесный способ
задания функции.
Проводим через произвольную точку
кривой прямую, параллельную оси
ординат. Если каждая такая прямая
пересекала линию только в одной
точке, то это график.
опрос
Фронтальная
Решение домашнего задания.
№8.30.
а) у 
х 2  36
х2  х  2
х2-36≥0;
х2-х-2>0;
х1=-2;
х2=3;
х3=-6;
х4=6.
+
-6
+
-2
-
6
3
+
+
D(f)=(-∞;-6]∪[6;+∞).
б) у 
х 2  6х  5
25  х 2
х2-6х+5≥ 0;
25-х2>0;
х1=5;
х2=1;
х3=-5;
х4=5.
+
1
-
5
+
- -5
+
5 -
-
2
+
2 -
D(f)=(-5;1]
в) у 
х2  4
6  х  х2
х2-4≥ 0;
6-х-х2>0;
х1=-2;
х2=2;
х3=-3;
х4=2.
+
- -3
D(f)=(-3;-2]
г) у 
х2  7х  8
9  х2
х2+7х-8≥ 0;
9-х2>0;
-2
+
х1=-8;
х2=1;
х3=-3;
х4=3.
+
-8
- -3
-
1
+
+
3 -
D(f)=[1;3).
№ 9.11. Функция задана формулой s=2t2+4t,где t – время (в ч), s – путь (в км).
a)s(1)=2+4=6
s(2,5)=2*6,25+4*2,5=22,5
s(4)=2*16+4*4=48
б)s=240 км, 2t2+4t=240;
t2+2t-120=0
t1=10
t2=-12/
в)t=45, s=2*452+4*45=4050+180=4230.