Районный конкурс поделок « В мире многогранников» Руководитель: Изъюрова Тамара Александровна
реклама

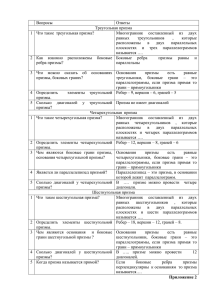
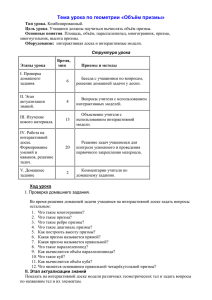
Районный конкурс поделок « В мире многогранников» Авторы: Кашин Петр Андреевич, Никитин Даниил Викторович (ученики 7 класс) Руководитель: Изъюрова Тамара Александровна Образовательная организация: МКОУ Чантырская СОШ Название работы: Замок Кастель-дель- Монте Замок Кастель-дель-Монте (итал. Castel del Monte — «замок на горе») расположен на юге Италии, в городе Андрия (Andria), в провинции Бари, в регионе Апулия. Кастель-дель-Монте — это один из самых выдающихся замков времён императора Фридриха II, который также признан памятником Всемирного наследия ЮНЕСКО. Ещё одно название замка — «Корона Апулии». Император был одним из самых образованных людей своего времени, знал греческий, арабский и латинский языки. При дворе Фридриха устраивались математические состязания, в которых принимал участие Фибоначчи, что возможно, в какой-то мере повлияло и на строгие архитектурные формы Кастель-дельМонте. В Кастель-дель-Монте два этажа с плоской крышей. Снаружи замок представляет собой правильную восьмиугольную призму, сторона основания которой 16,5 метров. На каждом углу здания находится башня, так же имеющая форму правильной восьмиугольной призмы, стороны основания башен - порядка 3,1м. Высота стен – 25м, высота башен – 26м. Конструкция замка имеет следующую особенность – две стороны башни состыкованы с одной из сторон основного восьмиугольника. Строго посередине высоты по всему периметру проходит небольшой карниз, который разделяет этажи друг от друга. Внутренний двор — это также правильный восьмиугольник. Об этом замке мы упоминали в нашей исследовательской работе «Удивительное число Пи», которую мы представили на районной конференции «Шаг в будущее». Поэтому изготовление модели этого замка является продолжением нашей работы. Изображение замка, исторические сведения, размеры мы нашли на сайте http://www.allcastles.ru/italy/castel-del-monte. Модель замка изготовлена нами в масштабе 1:200 из альбомных листов. Для изготовления модели мы сделали 8 правильных восьмиугольных призм (это башни) и одну большую правильную восьмиугольную призму. ПРИЗМА — многогранник, две грани которого (основания) — равные многоугольники, расположенные в параллельных плоскостях, а другие грани (боковые) — параллелограммы. Призма называется прямой, когда боковые ребра призмы перпендикулярны основаниям. Прямая призма называется правильной, если в ее основания лежат правильные многоугольники. Боковые грани призмы — параллелограммы. Параллелепипед - призма, в основании которой находится параллелограмм. Параллелепипеды, как и всякие призмы, могут быть прямые и наклонные. Наклонный параллелепипед - это наклонная призма, в основании которой параллелограмм . Прямой параллелепипед - это прямая призма, в основании которой параллелограмм или параллелепипед, у которого боковое ребро перпендикулярно плоскости основания. Прямоугольный – это прямой параллелепипед, в основании которого прямоугольник (или прямая призма, в основании которой лежит прямоугольник). Основания призмы являются равными многоугольниками. Боковые грани призмы являются параллелограммами. Боковые ребра призмы параллельны и равны Объём призмы равен произведению её высоты на площадь основания: Площадь полной поверхности призмы равна сумме площади её боковой поверхности и удвоенной площади основания. Площадь боковой поверхности произвольной призмы , где — периметр перпендикулярного сечения, — длина бокового ребра. Площадь боковой поверхности прямой призмы , где — периметр основания призмы, — высота призмы. Перпендикулярное сечение перпендикулярно ко всем боковым рёбрам призмы. Углы перпендикулярного сечения — это линейные углы двугранных углов при соответствующих боковых рёбрах. Перпендикулярное сечение перпендикулярно ко всем боковым граням. https://ru.wikipedia.org/wiki/Призма_(геометрия) Предметы, имеющие форму призмы, встречаются в природе (например, пчелиные соты, кристаллы), в архитектуре, в бытовых предметах, в технике(некоторые детали механизмов)