Приложение №2. Решение уравнений (опорный конспект). Вид уравнения,
реклама
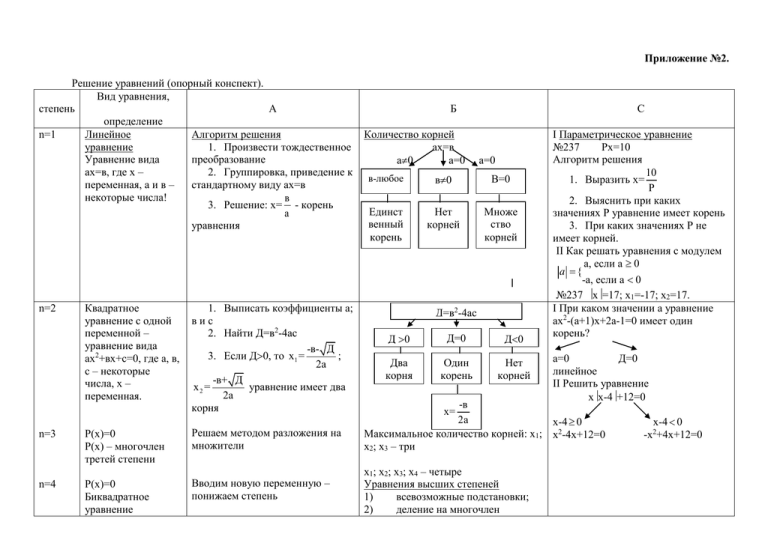
Приложение №2. Решение уравнений (опорный конспект). Вид уравнения, степень А определение n=1 Линейное Алгоритм решения уравнение 1. Произвести тождественное Уравнение вида преобразование ах=в, где х – 2. Группировка, приведение к переменная, а и в – стандартному виду ах=в некоторые числа! в 3. Решение: х= - корень а уравнения n=2 Квадратное уравнение с одной переменной – уравнение вида ах2+вх+с=0, где а, в, с – некоторые числа, х – переменная. 1. Выписать коэффициенты а; вис 2. Найти Д=в2-4ас -в- Д 3. Если Д0, то х1 = ; 2а -в+ Д х2 = уравнение имеет два 2а корня n=3 Р(х)=0 Р(х) – многочлен третей степени Решаем методом разложения на множители n=4 Р(х)=0 Биквадратное уравнение Вводим новую переменную – понижаем степень Б Количество корней ах=в а0 а=0 С а=0 в-любое в0 В=0 Единст венный корень Нет корней Множе ство корней Д=в2-4ас Д 0 Д=0 Д0 Два корня Один корень Нет корней I Параметрическое уравнение №237 Рх=10 Алгоритм решения 10 1. Выразить х= Р 2. Выяснить при каких значениях Р уравнение имеет корень 3. При каких значениях Р не имеет корней. II Как решать уравнения с модулем а, если а 0 а -а, если а 0 №237 х=17; х1=-17; х2=17. I При каком значении а уравнение ах2-(а+1)х+2а-1=0 имеет один корень? а=0 Д=0 линейное II Решить уравнение хх-4+12=0 -в 2а х-4 0 Максимальное количество корней: х1; х2-4х+12=0 х2; х3 – три х= х1; х2; х3; х4 – четыре Уравнения высших степеней 1) всевозможные подстановки; 2) деление на многочлен х-4 0 -х +4х+12=0 2 3) метод неопределённых коэффициентов




