Космические методы определения системы

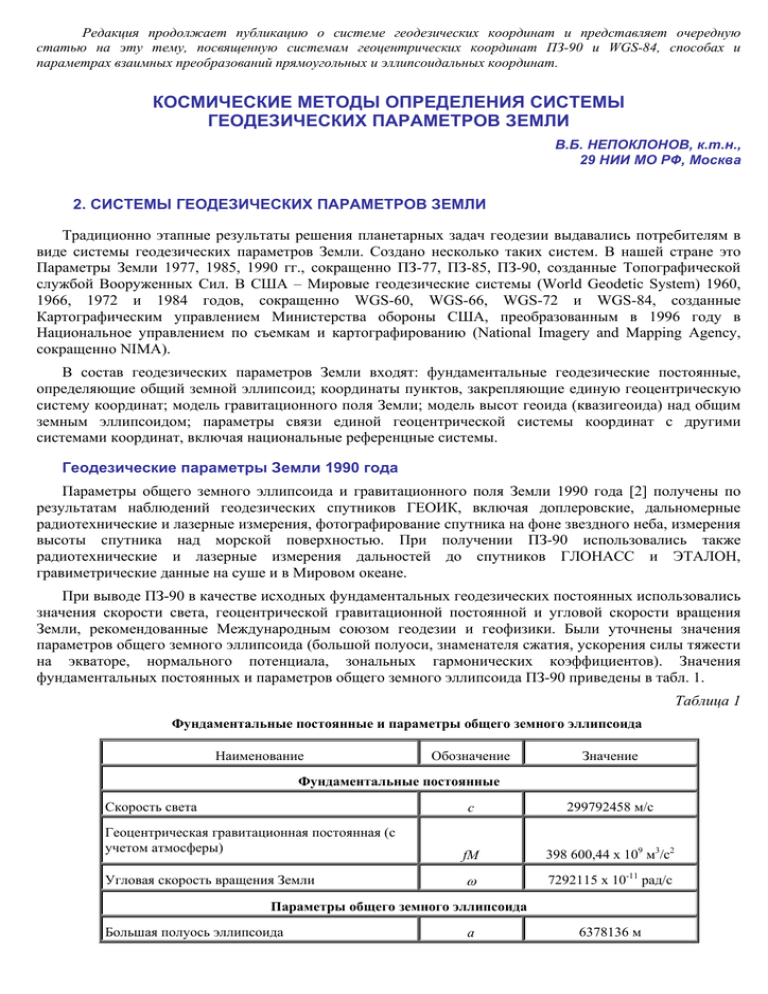
Редакция продолжает публикацию о системе геодезических координат и представляет очередную
статью на эту тему, посвященную системам геоцентрических координат ПЗ-90 и WGS-84, способах и
параметрах взаимных преобразований прямоугольных и эллипсоидальных координат.
КОСМИЧЕСКИЕ МЕТОДЫ ОПРЕДЕЛЕНИЯ СИСТЕМЫ
ГЕОДЕЗИЧЕСКИХ ПАРАМЕТРОВ ЗЕМЛИ
В.Б. НЕПОКЛОНОВ, к.т.н.,
29 НИИ МО РФ, Москва
2. СИСТЕМЫ ГЕОДЕЗИЧЕСКИХ ПАРАМЕТРОВ ЗЕМЛИ
Традиционно этапные результаты решения планетарных задач геодезии выдавались потребителям в
виде системы геодезических параметров Земли. Создано несколько таких систем. В нашей стране это
Параметры Земли 1977, 1985, 1990 гг., сокращенно ПЗ-77, ПЗ-85, ПЗ-90, созданные Топографической
службой Вооруженных Сил. В США – Мировые геодезические системы (World Geodetic System) 1960,
1966, 1972 и 1984 годов, сокращенно WGS-60, WGS-66, WGS-72 и WGS-84, созданные
Картографическим управлением Министерства обороны США, преобразованным в 1996 году в
Национальное управлением по съемкам и картографированию (National Imagery and Mapping Agency,
сокращенно NIMA).
В состав геодезических параметров Земли входят: фундаментальные геодезические постоянные,
определяющие общий земной эллипсоид; координаты пунктов, закрепляющие единую геоцентрическую
систему координат; модель гравитационного поля Земли; модель высот геоида (квазигеоида) над общим
земным эллипсоидом; параметры связи единой геоцентрической системы координат с другими
системами координат, включая национальные референцные системы.
Геодезические параметры Земли 1990 года
Параметры общего земного эллипсоида и гравитационного поля Земли 1990 года [2] получены по
результатам наблюдений геодезических спутников ГЕОИК, включая доплеровские, дальномерные
радиотехнические и лазерные измерения, фотографирование спутника на фоне звездного неба, измерения
высоты спутника над морской поверхностью. При получении ПЗ-90 использовались также
радиотехнические и лазерные измерения дальностей до спутников ГЛОНАСС и ЭТАЛОН,
гравиметрические данные на суше и в Мировом океане.
При выводе ПЗ-90 в качестве исходных фундаментальных геодезических постоянных использовались
значения скорости света, геоцентрической гравитационной постоянной и угловой скорости вращения
Земли, рекомендованные Международным союзом геодезии и геофизики. Были уточнены значения
параметров общего земного эллипсоида (большой полуоси, знаменателя сжатия, ускорения силы тяжести
на экваторе, нормального потенциала, зональных гармонических коэффициентов). Значения
фундаментальных постоянных и параметров общего земного эллипсоида ПЗ-90 приведены в табл. 1.
Таблица 1
Фундаментальные постоянные и параметры общего земного эллипсоида
Наименование
Обозначение
Значение
Фундаментальные постоянные
Скорость света
Геоцентрическая гравитационная постоянная (с
учетом атмосферы)
Угловая скорость вращения Земли
с
299792458 м/c
fM
398 600,44 x 109 м3/с2
ω
7292115 x 10-11 рад/с
Параметры общего земного эллипсоида
Большая полуось эллипсоида
a
6378136 м
Знаменатель сжатия
Ускорение силы тяжести на экваторе
Поправка в ускорение силы тяжести за
притяжение атмосферы на уровне моря
Нормальный потенциал
Зональный гармонический коэффициент второй
степени
Зональный гармонический коэффициент второй
степени
f
298,257839303
γe
978032,8 мГал
δγ a
-0,9 мГал
U0
62636861,074 м2/с2
С20
-484164,953 x 10-9
C40
790,3 x 10-9
Точность отнесения системы координат ПЗ-90 к центру масс Земли характеризуется средними
квадратическими погрешностями 1-2 м. Взаимное положение пунктов в ПЗ-90 определяется с
погрешностью около 0,3 м. Контроль положения пунктов относительно центра масс Земли, выполненный
в 29 НИИ МО РФ с использованием метода Жонголовича, показал, что вероятные линейные смещения
начала системы координат ПЗ-90 относительно центра масс Земли по абсолютной величине не
превышают 1 м. Это согласуется с оценками точности определения геоцентрических координат пунктов
космической геодезической сети. Для контроля точности ориентировки космической геодезической сети
использовались данные регулярных определений координат полюса по информации спутников ГЕОИК.
Полученные результаты подтвердили приведенные выше характеристики точности координат пунктов.
Создание космической геодезической сети и ее объединение с астрономо-геодезической сетью позволило
существенно повысить точность государственной геодезической сети.
Гравитационное поле Земли ПЗ-90 описывается параметрами нормального и аномального
потенциалов.
Нормальный потенциал U представлен двумя способами: с использованием нормированных
гармонических коэффициентов второй и четвертой степени; с использованием системы семи точечных
масс, координаты и значения которых строго согласованы с гармоническими коэффициентами
нормального потенциала.
Аномальный (возмущающий) потенциал представлен в трех вариантах: в форме нормированных
коэффициентов разложения геопотенциала в ряд по сферическим функциям до 36-й степени и порядка; в
форме параметров 60-ти точечных масс; в форме параметров 320-ти точечных масс. В начале 1990-х
годов на основе этих моделей была получена модель аномального гравитационного поля Земли
повышенной точности в виде коэффициентов разложения геопотенциала в ряд по сферическим функциям
до 200-й степени и порядка. Точность представления гравитационного поля коэффициентами до
200-й степени в целом по земному шару характеризуется средней квадратической погрешностью
высот геоида 2 м, коэффициентами до 36-й степени и системой 320 точечных масс – 3 м, системой
60 точечных масс – 4 м.
Разнообразие форм представления гравитационного поля Земли позволяет выбрать потребителю
оптимальный вариант модели для решения конкретной задачи.
Новизна методологий и технологий решения комплекса научно-технических задач, связанных с
определением Параметров Земли 1990 года, состояла в следующем:
1. Реализована оптимальная по затратам программа создания космической геодезической сети –
фундаментальной основы для изучения формы, размеров и гравитационного поля Земли, координатновременного обеспечения решения задач геодезии, навигации, геофизики, океанографии и космической
картографии.
2. Разработаны уникальные по составу, структуре и форме представления модели геодезических
параметров Земли, в максимальной степени ориентированные на потребителя.
3. Разработаны принципиально новые методы и технологии решения фундаментальных задач
геодезии по созданию Единой геоцентрической системы координат, определению планетарных и
детальных характеристик гравитационного поля Земли, в полной мере обеспечивающие реализацию
возможностей отечественного космического геодезического комплекса ГЕОИК.
4. Разработаны методы и технологии эффективного использования геодезических параметров Земли в
системах ракетного оружия и военной техники, космических навигационных, картографических
системах, предназначенных для решения оборонных задач и гражданского использования в различных
отраслях экономики страны.
Параметры Земли 1990 года внедрены в системах управления ракетных комплексов стратегического
назначения морского и наземного базирования; в наземных комплексах управления и программноаппаратных комплексах всех типов аппаратуры потребителя глобальных спутниковых навигационных
систем ГЛОНАСС и «Цикада», в наземном комплексе управления космического комплекса
картографирования; при модернизации государственной геодезической сети России.
Постановлением Правительства Российской Федерации № 568 от 28 июля 2000 года геоцентрическая
система координат «Параметры Земли 1990 года» установлена в качестве единой государственной
системы координат для использования в целях геодезического обеспечения орбитальных полетов и
решения навигационных задач.
По основным параметрам система ПЗ-90 находится на уровне лучшей из аналогичных зарубежных
систем – Мировой геодезической системы 1984 года (WGS-84). Это нашло отражение в рекомендациях
Международной организации гражданской авиации (ICAO) и Международной морской организации
(IMO) использовать ПЗ-90 и WGS-84 в качестве основных геодезических систем в комбинированных на
базе ГЛОНАСС и глобальных спутниковых навигационных GPS-системах.
Мировая геодезическая система 1984 года
Мировая геодезическая система 1984 года (WGS-84) [5], созданная в США по материалам
наблюдений более чем 30-ти ИСЗ, считается лучшей из зарубежных систем геодезических параметров
Земли (с учетом ее модернизаций, проведенных в последние годы). Определяющими фундаментальными
геодезическими постоянными системы WGS-84 являются: большая полуось общего земного эллипсоида
a=6378137,0 м; геоцентрическая гравитационная постоянная fM, значение которой (с учетом атмосферы)
было принято равным 398600,4418x10-9; нормированный второй зональный гармонический коэффициент
С20 = -484164,953x10-9; угловая скорость вращения Земли ω = 7292115.0 x 10-11 рад/с.
Первоначальная реализация WGS-84 основывалась на наблюдениях начала 80-х годов. C развитием
GPS были предложены новые методы определения местоположения, точность которых существенно
превышала точность WGS-84. Исследования, проведенные министерством обороны США, показали, что
благодаря уточнению WGS-84 можно существенно улучшить методику определения орбит спутников
GPS. В 1993-1994 гг. появились новые требования к точности WGS-84 со стороны геодезических
пользователей GPS. Было признано, что создание точной сети геодезических контрольных станций
поможет выполнению указанных требований. По этой причине Картографическое управление МО США
систематизировало все требования к повышению точности WGS-84 и в середине 1993 года осуществило
специальную программу, имеющую целью улучшение WGS-84. В июне 1994 г. была введена новая
версия WGS-84, получившая наименование WGS-84 (G730). В этой версии используются уточненные
координаты пунктов слежения МО США за спутниками GPS, что привело к согласию системы координат
WGS-84 с системой ITRF на уровне 10 см. Картографическое управление МО США приступило также к
работе по уточнению модели гравитационного поля Земли и геоида. Последняя из модификаций WGS-84
характеризуется ошибкой отнесения системы координат к центру масс Земли 1-2 метра, взаимного
положения геодезических пунктов 0,1 м. Особенностью современной версии WGS-84 является
включение в состав этой системы новой глобальной модели гравитационного поля Земли EGM-96
повышенной точности и пространственного разрешения, созданной совместными усилиями
Национального управления США по съемкам и картографированию, Годдардовского центра
космических полетов НАСА и Университета штата Огайо. Модель EGM-96 представляет полный набор
коэффициентов разложения геопотенциала в ряд сферических функций до 360-й степени. В усеченном
(до 70-й степени) виде данная модель рекомендуется для использования в высокоточных орбитальных
определениях. Кроме этого, гравитационное поле представлено глобальной цифровой моделью высот
геоида на сетке 15'×15'. Современный уровень точности определения высот геоида в целом по земному
шару характеризуется средними квадратическими погрешностями, лежащими в диапазоне от 0,5 до 1
метра.
Связь систем координат ПЗ-90 и WGS-84
При выполнении геодезических, навигационных, картографических работ с использованием
аппаратуры потребителей радионавигационных систем ГЛОНАСС и GPS возникает необходимость
преобразования координат и их приращений из одной системы (ПЗ-90, WGS-84) в другую. Методы
преобразований координат и их приращений из одной системы в другую, а также порядок использования
численных значений элементов трансформирования систем координат установлены ГОСТом P 51794 –
2001 «Аппаратура радионавигационная глобальной навигационной спутниковой системы и глобальной
системы позиционирования. Системы координат. Методы преобразований координат определяемых
точек».
Преобразование пространственных прямоугольных координат X, Y, Z из системы I в систему J
описывается формулой Гельмерта:
()
⎛ 1
X
⎜
Y
= (1 + m) ⎜ −ω
Z
⎜
Z J
⎜ω
⎝ Y
где
()
−ω Y ⎞ X
⎟
ωX ⎟ Y +
⎟
1 ⎟ Z I
⎠
ωZ
1
−ω X
⎛ ∆x ⎞
⎜∆y⎟ ,
⎜ ⎟
⎜ ∆z ⎟
⎝ ⎠
(1)
∆x, ∆y, ∆z – линейные элементы трансформирования;
ωx, ωy, ωz – угловые элементы трансформирования;
m – дифференциальное различие масштабов систем координат.
Формула обратного преобразования имеет вид:
()
⎛ 1
X
⎜
= (1 − m) ⎜ ω
Y
⎜ Z
Z I
⎜ −ω
⎝ Y
()
ωY ⎞ X
⎟
−ω Z
⎛ ∆x ⎞
.
− ⎜∆y ⎟
−ω X ⎟ Y
⎜
⎟
⎟
⎜ ⎟
1 ⎟ Z J ⎝ ∆z ⎠
⎠
1
ωX
(2)
Прямое и обратное преобразование геодезических координат В, L, H выполняют по формулам:
BI + ∆ B ⎫
⎪⎪
LJ = LI + ∆ L ⎬ ,
⎪
H J = H I + ∆ H ⎪⎭
BJ
где
∆B, ∆L, ∆H –
=
(3)
поправки к соответствующим координатам.
Поправки ∆B, ∆L, ∆H в (3) получают из выражений:
∆B =
⎛N
N 2
e sin B cos B∆a + ⎜ 2
[
(M + H ) a
⎞
∆e 2
+ 1 ⎟ N sin B cos B
−
2
⎝a
⎠
2
ρ ′′
]
−( ∆ x cos L + ∆ y sin L)sin B + ∆ z cos B −
(
)
(
)
−ω x sin L 1 + e 2 cos 2 B + ω y cos L 1 + e 2 cos 2 B − ρ me 2 sin B cos B;
∆L =
ρ ′′
( N + H ) cos B
( − ∆ x sin L + ∆ y cos L) + tgB (1 − e 2 )(ω x cos L +
(4)
+ω y sin L) − ω z ;
∆H = −
a
∆e 2
+ ( ∆ x cos L + ∆ y sin L) cos B + ∆ z sin B −
∆a + N sin 2 B
N
2
− Ne 2 sin B cos B (
ωy
⎛ a2
⎞
ωx
sin L −
cos L) + ⎜ + H ⎟ m;
ρ
ρ
⎝N
⎠
∆a = a J − a I ; ∆e2 = eJ2 − eI2 ; a =
(
)
1
1
( aJ + aI ) ; e = eJ2 + eI2 ;
2
2
M=
где
(
a 1 − e2
(1 − e
2
)
sin 2 B
)
3
; N=
,
a
2
2
1 − e sin B
B, L, H – геодезические координаты (широта, долгота, высота);
aI , aJ – большие полуоси эллипсоидов в системах координат I, J;
eI2 , eJ2 – квадраты эксцентриситетов эллипсоидов в системах координат I, J;
М, N – радиусы кривизны меридианального сечения и первого вертикала
эллипсоида;
ρ" – число угловых секунд в одном радиане (ρ" = 206264,8062").
Формулы (4) обеспечивают получение поправок к геодезическим координатам с погрешностью, не
превышающей 0,3 м. Второе приближение при:
B = BI + ∆ B / 2
(5)
⎫
⎪⎪
L = LI + ∆ L / 2 ⎬
⎪
H = H I + ∆ H / 2⎪⎭
позволяет уменьшить погрешность преобразования (3) до 0,001 м.
Альтернативный способ предполагает получение геодезических координат через пространственные
прямоугольные координаты.
При этом сначала переходят от геодезических координат к прямоугольным координатам в исходной
системе по формулам:
X = ( N + H ) cos B cos L ⎫
⎪
Y = ( N + H ) cos B sin L ⎬ ,
⎪
Z = [(1 − e2 ) N + H ]sin B ⎭
где
X, Y, Z –
(6)
прямоугольные координаты;
B, L, H – геодезические координаты (широта, долгота, высота);
N – радиус кривизны первого вертикала;
e – эксцентриситет эллипсоида.
Затем выполняют преобразование прямоугольных координат в другую систему по формулам (1),
после чего осуществляют обратный переход от полученных прямоугольных координат к геодезическим
координатам.
Пространственные прямоугольные координаты X , Y , Z могут быть преобразованы в геодезические
координаты B, L, H с использованием следующего алгоритма.
Вычисляют вспомогательную величину:
(7)
D = X 2 +Y 2 .
В случае D=0 полагают:
⎧π
⎪⎪ , если Z > 0,
B = ⎨2
⎪ − π , если Z < 0;
⎪⎩ 2
L = 0;
H = Z sin B − a 1 − e2 sin 2 B .
В случае D>0 долготу получают как:
(8)
⎧ L ',
⎪ 2π − L ',
⎪
L=⎨
⎪π − L ',
⎪⎩π + L ',
если X > 0, Y > 0,
если X > 0, Y < 0,
(9)
если X < 0, Y > 0,
если X < 0, Y < 0,
где L ' = arcsin ⎛⎜ Y ⎞⎟ ,
⎝D⎠
(10)
а для определения широты и высоты анализируют значение Z.
Если Z=0, полагают:
B = 0; H = D − a.
(11)
В остальных случаях широту получают итеративным путем по формулам:
⎛Z⎞
Bi = arcsin ⎜ ⎟ + δ Bi ;
⎝r⎠
⎛
(12)
⎞
⎟;
⎜ r 1 − e2 sin 2 B ⎟
i ⎠
⎝
δ Bi +1 = arcsin ⎜
ae2 sin 2 Bi
r = X 2 +Y 2 + Z2.
Где i –
номер приближения (i = 0, 1, …).
Вычисления по формулам (12) начинают при δ B = 0 и повторяют до выполнения условия
Bi +1 − Bi < ε , где ε – установленный допуск (ε=0,0001"). Окончательно:
B = Bi ;
(13)
H = D cos B + Z sin B − a 1 − e2 sin 2 B ,
причем погрешность вычисления высоты не превышает 0,003 м.
Реализация формул преобразования координат предполагает, что известны семь элементов
трансформирования ∆x, ∆y , ∆z, ω X , ωY , ω Z , m . Определение этих параметров представляет собой
отдельную задачу, решение которой получают следующим способом.
Из соотношений (1) следует, что разности координат пунктов в различных системах выражаются в
виде:
⎛ ∆X ⎞ ⎛ 1 0 0 X
⎜ ∆Y ⎟ = ⎜ 0 1 0 Y
⎜
⎟ ⎜
⎜
⎟ ⎜
⎝ ∆Z ⎠ ⎝ 0 0 1 Z
0
Z
−Y
−Z
0
X
⎛ ∆x
⎜ ∆y
⎜
Y ⎞ ⎜ ∆z
⎜
−X ⎟⎜m
⎟
0 ⎠⎟ ⎜ ω X
⎜
⎜ ωY
⎜ω
⎝ Z
⎞
⎟
⎟
⎟.
⎟
⎟
⎟
⎟
⎟
⎟
⎠
(14)
Элементы трансформирования могут быть получены из решения системы уравнений вида (14) для
достаточного набора пунктов по методу наименьших квадратов с учетом матрицы весов,
характеризующей точность знания координат пунктов в обеих системах.
Надежность определения параметров связи систем координат WGS-84 и ПЗ-90 указанным способом
зависит от двух основных факторов.
Одним из них является число и оптимальность географического расположения исходных пунктов.
Для глобального распространения элементов связи географическое распределение исходных пунктов
также должно быть глобальным.
Вторым условием является обеспечение точного определения координат исходных пунктов в двух
названных системах. В каждой системе координат имеются так называемые опорные пункты,
координаты которых определяют наилучшим образом из обработки достаточно больших объемов
высокоточной спутниковой траекторной информации за продолжительный период времени наблюдений.
Точность определения положения опорных пунктов в геоцентрической системе характеризуется
средними квадратическими погрешностями 1-2 м по каждой составляющей. Ведутся регулярные работы
по повышению точности координат опорных пунктов. Кроме этого, координаты могут быть получены с
использованием геодезической аппаратуры потребителя навигационных систем GPS/ГЛОНАСС. Однако
точность навигационных определений, базирующихся на бортовых эфемеридах спутников, недостаточна
для выполнения современных требований к определению параметров связи двух систем координат. Для
получения надежных параметров связи систем координат ПЗ-90 и WGS-84 необходимо выполнять
обработку полученной с использованием такой аппаратуры измерительной информации ГЛОНАСС
орбитальным методом с одновременным уточнением орбит спутников и координат приемников. В этом
случае может быть обеспечено определение координат пунктов в системе ПЗ-90 с погрешностью 1 м и
точнее. Для получения координат в системе WGS-84 с такой же точностью при обработке измерительной
информации GPS использовать точные эфемериды, которые стали доступными в последние годы.
Важным вопросом при определении параметров связи является оценка точности как самих
параметров, так и преобразования координат с их использованием. Точность параметров связи
оценивают с помощью ковариационной матрицы К, равной обратной матрице системы нормальных
уравнений с точностью до постоянного множителя, определяемого специальным образом. Точность
BKBT , где В – матрица
преобразования координат характеризуют ковариационной матрицей
преобразования (14).
Наиболее высокая точность определения параметров связи систем координат ПЗ-90 и WGS-84 в
настоящее время может быть достигнута путем привязки опорных пунктов ПЗ-90 к пунктам сети WGS-84
(или ITRF) либо пунктов WGS-84 к пунктам ПЗ-90 с использованием точных эфемерид спутников
ГЛОНАСС и GPS.
К настоящему времени опубликовано несколько вариантов параметров связи ПЗ-90 и WGS-84,
отличающихся не только значениями, но и методами получения. Заслуживающие внимания результаты
приведены в сводной таблице 2.
Таблица 2
Параметры связи ПЗ-90 и WGS-84 (по данным различных источников)
Вариант Год
∆x , м ∆y , м
∆z ,
m,
м
ед. 6-го зн.
ωX ,
ωY ,
ωZ ,
сек.
сек.
сек.
1
1993
0
0
+1,5
0
0
0
-0,076
2
1994
0
0
+4,0
0
0
0
-0,6
3
1995
-0,3
+2,2
+1,0
-0,06
-0,05
-0,01
-0,07
4
1996
0
+2,5
0
0
0
0
-0,4
5
1996
0
0
+1,0
0
0
0
-0,2
6
1997
+1,08
+0,27
+0,90
0,125
0
0
+0,16
Вариант 1 получен специалистами Топографической службы ВС РФ на основе опыта создания
геоцентрической системы координат ПЗ-90 [6].
Варианты 2, 4 получены зарубежными специалистами по координатам спутников ГЛОНАСС в двух
системах координат [7, 8]. При этом координаты спутников ГЛОНАСС в системе ПЗ-90 взяты из
бортовых эфемерид, а в системе WGS-84 получены по специальным траекторным измерениям,
распределенным глобально. С учетом особенностей обработки измерительной информации и характера
влияния орбитальных погрешностей эти результаты считаются недостаточно надежными [3].
Вариант 3 получен ЦНИИГАиК с использованием результатов определений координат пунктов на
территории России по наблюдением спутников ТРАНЗИТ в период 1979–1994 гг. с учетом перехода от
системы координат WGS-82 к WGS-84 [9]. Полученные параметры связи практически эквивалентны
варианту 1, т.е. для территории России дают идентичные поправки при переходе от одной системы к
другой.
Параметры связи в варианте 5 определены с использованием новых данных, полученных в России с
использованием совмещенного приемника сигналов ГЛОНАСС/GPS [3].
Появление высокоточной спутниковой навигационной геодезической аппаратуры и программного
обеспечения, позволяющих определять взаимное положение пунктов, удаленных до нескольких тысяч
километров, с точностью на уровне 10-8 , позволило в 1997 году осуществить уточнение параметров связи
систем координат ПЗ-90 и WGS-84, основанное на прямом сравнении координат совмещенных пунктов.
В рамках данного проекта использована измерительная информация с восьми пунктов наблюдения,
расположенных по территории России (см. рисунок).
8
4
5
1
6
2
3
7
Схема размещения совмещенных пунктов
Полученная измерительная информация была обработана с использованием программного средства
обработки навигационных измерений на сверхдлинных базах GAMIT, включая уравнивание по
программе GLOBK. Это позволило определить координаты восьми пунктов в системе WGS-84 с
дециметровой точностью взаимного положения. Указанные пункты были привязаны к ближайшим
восьми пунктам космической геодезической сети, определенным в геоцентрической системе координат
ПЗ-90. Точность привязки выдержана на уровне 0,1 м. Таким образом, координаты совмещенных пунктов
были получены как в системе WGS-84, так и системе ПЗ-90. С использованием разностей координат по
описанной выше методике были определены параметры связи двух систем координат. Наиболее
достоверные из полученных результатов приведены в последней строке табл. 2. Полученные элементы
трансформирования наилучшим образом подходят к территории России и прилегающим к ней территориям,
обеспечивая пересчет координат из ПЗ-90 в WGS-84 и обратно с погрешностью (3 σ) менее 1 м.
Литература
1. Стандартная Земля. Под ред. К. Лунквиста и Г.Вейса. Пер. с англ. М., «Мир», 1969.
2. Параметры общего земного эллипсоида и гравитационного поля Земли (Параметры Земли 1990 года).
М., РИО ТС ВС РФ, 1991.
3. Галазин В.Ф. и др. Система геодезических параметров Земли «Параметры Земли 1990 года» (ПЗ-90).
М., КНИЦ, 1998.
4. Галазин В.Ф., Зуева А.Н., Македонский Е.Л. и др. Опыт создания планетарных моделей
гравитационного поля Земли с использованием ГЕО-ИК. «Геодезия и картография». 1993, № 11.
5. World Geodetic System 1984 / Defense Mapping Agency Technical Report DMATR 8350.2, Second Edition
– Department of Defence, 1991.
6. Бойков В.В., Галазин В.Ф., Каплан Б.Л. и др. Опыт создания геоцентрической системы координат ПЗ90. «Геодезия и картография». 1993, № 11.
7. Mirsa P.N., Abbot R.I. SGS85-WGS84 Transformation // Manuscripta Geodaetica. 1994. Vol. 19.
8. Mirsa P.N., Abbot R.I., Gaposchkin E.M. Integrated use of GPS and GLONASS: Transformation between
WGS-84 and PZ-90. Pres. at the Inst. of Navigation, ION GPS-96.
9. Бовшин Н.А., Зубинский В.И., Остач О.М. Совместное уравнивание общегосударственных опорных
геодезических сетей. «Геодезия и картография». 1995, №8.