Задача 321: RC-генератор - Кафедра общей физики физфака МГУ

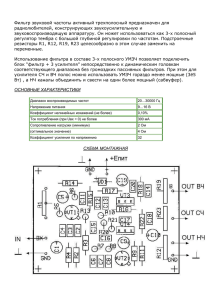
Московский государственный университет
им. М.В.Ломоносова
Физический факультет
Кафедра общей физики
Лабораторный практикум по
общей физике
(электричество и магнетизм)
Лабораторная работа № 321
RC-ГЕНЕРАТОР
ГАРМОНИЧЕСКИХ КОЛЕБАНИЙ
Буханов В.М.
Козлов В.И.
Матюнин А.В.
М О С К В А - 2011
Изучается принцип действия генератора гармонических колебаний RC-типа, экспериментально проверяются условия возбуждения генератора.
Принцип действия RC-генератора
Генераторы RC-типа применялись в радиоизмерительной аппаратуре звукового диапазона частот. Такое название они получили потому, что в них отсутствует колебательный
контур, а частота генерируемых колебаний определяется параметрами цепи обратной связи, состоящей из конденсаторов и резисторов. Основными достоинствами RC-генератора
являются простота схемы, надежность в работе, удобство настройки в широком диапазоне
частот и отсутствие в схеме сложных и громоздких деталей.
Принцип работы генератора состоит в следующем: пусть имеется усилитель, вход и
выход которого соединены цепью обратной связи. На рис. 1 дана блок-схема усилителя с
обратной связью.
Рис. 1. Блок-схема усилителя с обратной связью
В системе происходит циклический процесс, в котором флюктуационное (шумовое)
напряжение U усиливается до U 2 , поступает на вход цепи обратной связи, становясь U 3
на ее выходе, складывается с исходным напряжением U , давая в результате U 1 , с которым далее повторяется тот же процесс. Заметим, что на входе усилителя складываются
колебания, а не постоянные напряжения, и результат сложения зависит от разности фаз
этих колебаний. Подчеркнем еще раз, что U не напряжение, подаваемое от какого-либо
внешнего источника, а собственное шумовое колебание на входе усилителя.
Введем следующие обозначения:
U 2 / U1  K - коэффициент усиления без обратной связи;
U 3 /U 2   - коэффициент обратной связи;
U 2 / U  K ' - коэффициент усиления с обратной связью.
Тогда из равенства U1  U  U 3 получим
K' 
K
. (1)
1  K
1
В формуле (1), если фазы U и U 3 совпадают, то  положительно, если фазы противоположны, то  отрицательно. Заметим, что если в цепи обратной связи отсутствуют какиелибо ЭДС (цепь пассивна), то 0    1.
Из анализа формулы (1) следует, что при   0 K  K '   . Значение K ' =  получается при  = 1/K. Это значение будем называть критическим. Усилитель с положительной обратной связью (  0), большей критической (  1/K), способен к автоколебаниям, т.е. является генератором незатухающих колебаний. Действительно, на входе любого
усилителя возникают хотя бы слабые тепловые флюктуации напряжения (шумы), имеющие сплошной (“белый”) спектр частот колебаний. Пройдя через усилитель и цепь обратной связи, эти колебания вернутся на вход усилителя уже с амплитудой, большей исходной (так как при   1/K U 3 > U 1 ).
При определенных условиях такой процесс приведет к нарастанию амплитуды колебания некоторой частоты (из сплошного шумового спектра), пока она не будет ограничена
нелинейностью характеристик транзисторов усилителя. Такими условиями самовозбуждения являются следующие два. Во-первых, фаза напряжения на выходе цепи обратной
связи должна совпадать с фазой входного напряжения усилителя (положительная обратная связь) - условие баланса фаз. Во-вторых, амплитуда напряжения на выходе цепи обратной связи должна превышать амплитуду первичного входного напряжения – условие
баланса амплитуд.
Чтобы колебания были близки по форме к гармоническим, необходимо выполнение
условий самовозбуждения в узком интервале частот.
Рассмотрим работу схемы RC-генератора (рис. 2).
Рис. 2. Схема RC-генератора
В этой схеме применен двухкаскадный транзисторный усилитель. Такой усилитель для
средней части своей амплитудно-частотной характеристики практически не поворачивает
фазу выходного напряжения (см. упражнение 4).
2
Используем метод комплексных амплитуд и правила Кирхгофа. Для этого заранее
предположим, что в генераторе установились синусоидальные электрические колебания с
некоторой круговой частотой . Комплексные амплитуды напряжения на входе и выходе


цепи обратной связи обозначим соответственно U 2 и U 3 .
Применим первое правило Кирхгофа в точке D (см. рис. 2):



U
I  I 1  I 2 , где I 1 = 3 , I 2 = U 3 (iC 2 ) ,
R2




или


1
+ iC 2 ). (2)
R2
I = U3(



Здесь I , I 1 , I 2 - комплексные амплитуды токов в соответствующих участках цепи, i –
мнимая единица.
Применим второе правило Кирхгофа к контуру, включающему R1 , C1 , а также вход и
выход цепи обратной связи (мысленно замыкаем их входным и выходным импедансами


усилителя, напряжения на которых U 3 и U 2 , соответственно):


U 2 = I ( R1 +

1
) + U3.
iC1

Подставим сюда I из уравнения (2):


U 2 = U 3 [( R1 +
1
1
)(
+ iC 2 ) + 1],
iC1 R2
откуда


U 2 = U3[
R1
C
1
+ 2 + 1 + i( C 2 R1 
)]. (3)
R2
C1
C1 R2
Так как усилитель не поворачивает фазу напряжения, то условие баланса фаз будет выполняться, если цепь обратной связи также не будет поворачивать фазу, т.е. фазы U 2 и U 3
будут совпадать. Последнее будет иметь место, когда коэффициент при U 3 в формуле (3)
будет действительным числом. Для этого необходимо, чтобы
3
C 2 R1 
1
= 0.
C1 R2
Разрешив это равенство относительно  2 , получим
2 =

1
1
, =
=
R1 R2 C1C 2
2
2
1
. (4)
R1 R2 C1C 2
Таким образом, мы определили частоту , для которой выполняется условие баланса
фаз.
Коэффициент обратной связи при соблюдении условия баланса фаз из уравнения (3)
будет равен

U
U
1
 = 3 = 3 =
.
R
/
R

C
/
C

1
U2
1
2
2
1
U2
Условие баланса амплитуд   1/K для нашего случая запишется так:
R
C
1
 1/K, или K  1 + 2 + 1.
R2
C1
R1 / R2  C 2 / C1  1
Наименьшим значением для K, начиная с которого в генераторе смогут возникнуть автоколебания, очевидно, будет значение
K=
R1
C
+ 2 + 1. (5)
R2
C1
При R1  R2 и C1  C 2 , K = 3.
При значениях K, близких к наименьшему, генерируемое напряжение будет по своей
форме близко к синусоидальному, так как при этом условия самовозбуждения будут выполняться для узкого диапазона частот.
Описание экспериментальной установки
На рис. 3 изображена блок-схема установки. Общий вид экспериментальной установки
приведѐн на рис. 4.
4
Рис. 3. Блок-схема экспериментальной установки
Рис. 4. Общий вид экспериментальной установки
Транзисторный усилитель вместе с согласующими устройствами смонтирован на специальной панели (1). Цепь обратной связи также монтируется на отдельной панели (2).
Питание 8 В подается на усилитель от специального источника (3). Для наблюдения формы генерируемых колебаний, измерения их частоты и коэффициента усиления К имеется
осциллограф (4) и генератор напряжения звуковых частот (5). В качестве резистора R1 используется магазин сопротивлений (6), позволяющий устанавливать его значение в диапазоне 0.01 – 10 000 Ом, а в качестве R2 , C1 и C 2 - резисторы и конденсаторы, номиналы
которых даны в таблице, находящейся на рабочем столе установки. При выполнении работы обычно используются 2 резистора R2 и единственная комбинация C1 и C 2 .
5
Упражнение 1. ПРОВЕРКА УСЛОВИЯ БАЛАНСА ФАЗ
Собрать установку в соответствии со схемой рис. 3 (внешний генератор напряжения
пока не подсоединять). На панели для цепи обратной связи включить R2 , C1 , C 2 и магазин сопротивлений с первоначально установленным R1 = 0.
На экране осциллографа наблюдается генерируемый сигнал. Его форма заметно отличается от синусоидальной. Можно уменьшать коэффициент усиления К плавным вращением ручки потенциометра R пока не улучшится форма или не произойдет срыв генерации. В последнем случае вращением в обратную сторону восстанавливают генерацию,
оставляя К, при котором наблюдается устойчивая генерация. Регулировкой усиления осциллографа и частоты развертки устанавливают сигнал удобный для наблюдения.
При фиксированных значениях R2 , C1 и C 2 производится подбор максимально возможного значения R1 , при котором еще есть генерация. Отметим, что при такой настройке R1 генерируемый сигнал оказывается практически гармоническим.
Найденное значение R1 и установленные значения R2 , C1 и C 2 записываются в тетрадь;
по формуле (4) рассчитывается частота колебаний, отвечающая условию баланса фаз. Для
проверки этого условия необходимо измерить частоту генерируемых колебаний и сравнить ее с вычисленной.
Для этого на развертку осциллографа подается напряжение с внешнего генератора. Меняя его частоту, добиваемся получения эллипса на экране осциллографа, что свидетельствует о равенстве частоты развертки (ее значение находим на лимбе внешнего генератора) и измеряемой частоты. Совпадение в пределах ошибок частот измеренной и вычисленной по формуле (4) будет свидетельствовать о выполнении проверяемого условия.
Вышеуказанные измерения и вычисления повторяются для другого резистора R2 , имеющегося в комплекте установки.
Упражнение 2. УЧЕТ ВХОДНОГО СОПРОТИВЛЕНИЯ УСИЛИТЕЛЯ
После измерения частоты генерации с последним номиналом R2 , возвращаемся к внутренней развертке и удаляем R2 из схемы. Обычно эта операция не приводит к срыву колебаний, что следовало бы из (4) при R2 = ∞, – на экране остается колебание, однако его
форма сильно отличается от синусоидальной. Это говорит о том, что теперь роль R2 выполняет входное сопротивление усилителя (обозначим его Ri ). Повторяя процедуру подбора R1 и измерения частоты с помощью внешнего генератора, находим частоту, отвечающую этому сопротивлению; используя формулу (4), вычислим его значение. Если Ri
окажется сравнимым с номиналами ранее использованных резисторов R2 , следует скорректировать ранее проведенные вычисления частоты по формуле (4), учитывая, что R2
и Ri включены в схеме параллельно. Если Ri >> R2 , его нет необходимости учитывать, и
делается вывод о корректности расчетов в упражнении 1.
6
Упражнение 3. ПРОВЕРКА УСЛОВИЯ БАЛАНСА АМПЛИТУД
Для этой проверки необходимо измерить коэффициент усиления К, при котором производились все предыдущие измерения, и сравнить его с коэффициентом, вычисленным по
формуле (5) для каждой использованной комбинации параметров цепи обратной связи.
Поэтому, сохранив усиление, использованное при выполнении предыдущих измерений,
отключаем цепь обратной связи и подключаем внешний генератор к входу усилителя.
Амплитуду напряжения, подаваемого с генератора на вход усилителя, устанавливаем
такой, чтобы усилитель работал на линейном участке своей амплитудной характеристики,
т.е. не искажалась форма входного сигнала. Регулировки осциллографа установить так,
чтобы было удобно наблюдать сигнал на экране и измерять его амплитуду (в делениях
шкалы на экране).
Переключив осциллограф с выхода усилителя на его вход, измеряем амплитуду входного сигнала на экране осциллографа (в тех же делениях).
Отношение амплитуд сигнала на выходе и входе усилителя и есть коэффициент усиления:
К
U вых
.
U вх
Этот коэффициент сравниваем с К, вычисленным по формуле (5).
Упражнение 4. ПРОВЕРКА СИНФАЗНОСТИ НАПРЯЖЕНИЙ НА ВХОДЕ И
ВЫХОДЕ УСИЛИТЕЛЯ
При выводе формулы (4) для частоты генерации было принято, что усилитель не поворачивает фазу выходного напряжения ( U 1 и U 2 синфазны).
Проверить выполнение этого условия можно следующим образом. Напряжение с генератора подадим на вход усилителя (без обратной связи, как и в предыдущем упражнении)
и на внешнюю развертку осциллографа (вход Х). Напряжение с выхода усилителя подадим на вход осциллографа Y. На экране осциллографа наблюдается результат сложения
двух взаимно перпендикулярных колебаний одинаковой частоты. При произвольном соотношении фаз, это должен был бы быть эллипс, форма и ориентация которого относительно координатных осей зависят от разности фаз складываемых колебаний. В частности, для синфазных колебаний, эллипс вырождается в прямую линию, лежащую в первом
и третьем квадрантах, что и должно наблюдаться в нашем случае. Проверку следует проводить для частот, лежащих в тех же диапазонах, что и ранее определенные частоты генерации.
7
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Начертить блок-схему установки, объяснить работу RC-генератора.
2. В чем заключается условие самовозбуждения генератора?
3. От каких параметров зависит частота возбуждаемых колебаний? Каковы пределы изменения частоты генератора?
4. Какова природа исходных колебаний в RC-генераторе?
5. Чем обеспечивается положительность обратной связи?
6. Каким методом в данной задаче измеряется частота и коэффициент усиления К?
7. Как проверяется соотношение фаз колебаний на входе и выходе усилителя?
ЛИТЕРАТУРА
1. Матвеев А.Н., Электричество и магнетизм. М.: Высшая школа, 2005.
2. Калашников С.Г., Электричество. М.: Наука, 2008.
8