Документ 2627626

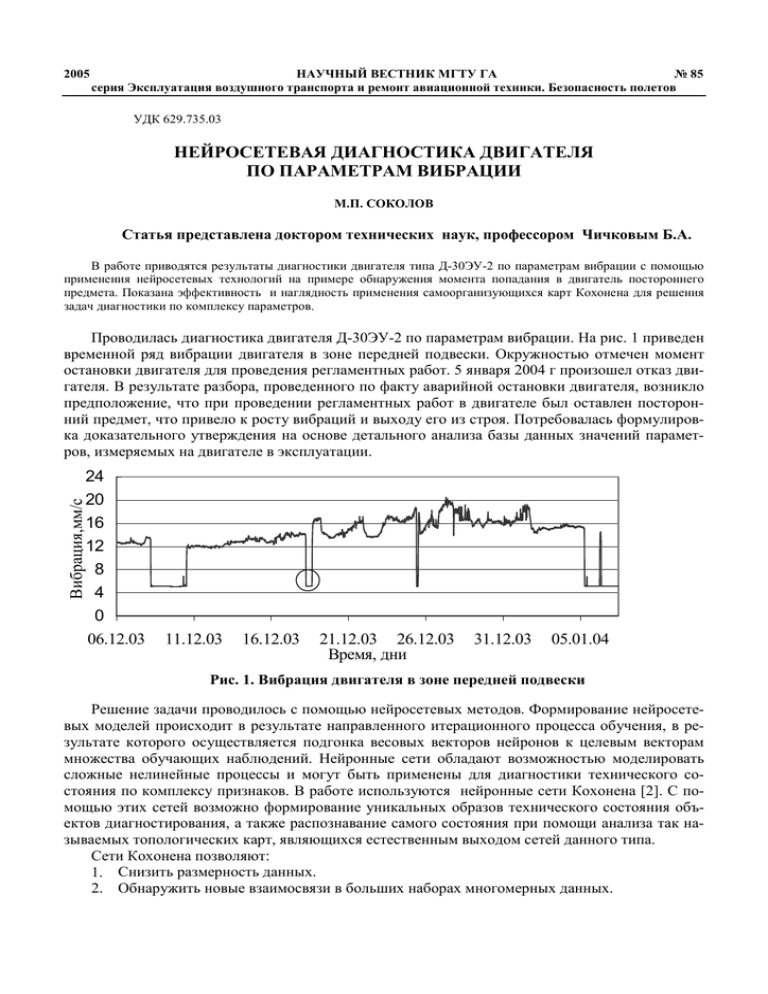
2005
НАУЧНЫЙ ВЕСТНИК МГТУ ГА
№ 85
серия Эксплуатация воздушного транспорта и ремонт авиационной техники. Безопасность полетов
УДК 629.735.03
НЕЙРОСЕТЕВАЯ ДИАГНОСТИКА ДВИГАТЕЛЯ
ПО ПАРАМЕТРАМ ВИБРАЦИИ
М.П. СОКОЛОВ
Статья представлена доктором технических наук, профессором Чичковым Б.А.
В работе приводятся результаты диагностики двигателя типа Д-30ЭУ-2 по параметрам вибрации с помощью
применения нейросетевых технологий на примере обнаружения момента попадания в двигатель постороннего
предмета. Показана эффективность и наглядность применения самоорганизующихся карт Кохонена для решения
задач диагностики по комплексу параметров.
Проводилась диагностика двигателя Д-30ЭУ-2 по параметрам вибрации. На рис. 1 приведен
временной ряд вибрации двигателя в зоне передней подвески. Окружностью отмечен момент
остановки двигателя для проведения регламентных работ. 5 января 2004 г произошел отказ двигателя. В результате разбора, проведенного по факту аварийной остановки двигателя, возникло
предположение, что при проведении регламентных работ в двигателе был оставлен посторонний предмет, что привело к росту вибраций и выходу его из строя. Потребовалась формулировка доказательного утверждения на основе детального анализа базы данных значений параметров, измеряемых на двигателе в эксплуатации.
Вибрация,мм/с
24
20
16
12
8
4
0
06.12.03
11.12.03
16.12.03
21.12.03 26.12.03
Время, дни
31.12.03
05.01.04
Рис. 1. Вибрация двигателя в зоне передней подвески
Решение задачи проводилось с помощью нейросетевых методов. Формирование нейросетевых моделей происходит в результате направленного итерационного процесса обучения, в результате которого осуществляется подгонка весовых векторов нейронов к целевым векторам
множества обучающих наблюдений. Нейронные сети обладают возможностью моделировать
сложные нелинейные процессы и могут быть применены для диагностики технического состояния по комплексу признаков. В работе используются нейронные сети Кохонена [2]. С помощью этих сетей возможно формирование уникальных образов технического состояния объектов диагностирования, а также распознавание самого состояния при помощи анализа так называемых топологических карт, являющихся естественным выходом сетей данного типа.
Сети Кохонена позволяют:
1. Снизить размерность данных.
2. Обнаружить новые взаимосвязи в больших наборах многомерных данных.
Нейросетевая диагностика двигателя по параметрам вибрации
139
3. Провести кластеризацию данных.
4. Выполнить визуализацию многомерных данных на двумерной плоскости.
Для решения задачи использовалась возможность сети к визуализации многомерных данных.
Алгоритм обучения нейронной сети состоял в следующем [3]:
1. Была проведена нормализация входных данных, см. формулу (1):
xi
xi`=
x21+x22+x23+…+x2k
,
(1)
где k – размерность пространства; xi – компонента входного вектора i.
2. Выбирались начальные значения весовых векторов нейронов. Компонентам весовых векторов присваивались малые случайные значения.
w = [w1, w2 ,…, wk] .
(2)
3. Из исходного набора данных случайно выбирался один из векторов и подавался на вход
нейронной сети.
4. Вычислялись выходы нейронов. Выход образовывается в результате скалярного перемножения вектора входных значений на вектор весов соответствующего нейрона в карте.
Yj = ∑ xi • wij ,
где wij – вес входа i нейрона j.
i
(3)
5. Выбирался нейрон «победитель». Нейроном «победителем» считается тот нейрон, выход
которого максимален. Скалярное произведение является мерой сходства между входным вектором и вектором весов.
6. Настраивались весовые вектора нейрона «победителя» и нейронов из его окрестности.
Wj(t+l) = Wj(t) + α[X – Wj(t)] ,
где: α – коэффициент скорости обучения.
(4)
Таким образом, процесс обучения состоял в выборе нейрона с весовым вектором, наиболее
близким к входному вектору, и дальнейшем приближении весового вектора к входному.
7. Возвращение к шагу 3. (Конец цикла обучения).
8. Одной эпохой обучения считалось предъявление сети всех наблюдений из обучающей
выборки (шаги с 3 по 7 повторенные n раз, где n – объем обучающей выборки). Алгоритм повторялся заданное число эпох.
Все расчеты, связанные с решением задачи при помощи нейронной сети, проводились с использованием стандартного пакета ST Neural Networks системы STATISTICA v.5.5 [1].
Компонентами входного вектора являлись значения параметров регистрируемых на двигателе. На вход сети подавались значения вибраций в зоне передней подвески, значения частоты
вращения ротора. Третьей компонентой вектора являлось время, в момент которого производилось соответствующее измерение значений параметров.
Входное множество данных формировалось из значений параметров, измеренных до и после проведения регламентных работ. Объем всего множества составил 1700 наблюдений (700
наблюдений до проведения регламентных работ, 1000 после).
Выбор количества элементов в выходном слое носил эмпирический характер и базировался
на следующих соображениях. Малое количество элементов в выходном слое не позволит качественно провести визуализацию множества входных данных. Чрезмерная же величина элемен-
М.П. Соколов
140
тов приведет к значительным затратам времени на обучение нейронной сети. Для решения задачи была выбрана структура сети Кохонена с 400 – ми элементами в выходном слое (квадрат
со стороной 20 элементов). Обучение сети Кохонена проводилось в два этапа. Настройки нейронной сети на этапах обучения (см. табл. 1) были рассчитаны на то, чтобы сначала получить
грубую картину визуализации трехмерного пространства исходных данных, а затем на оставшихся эпохах детализировать ее.
Таблица 1
Характеристики настройки сети Кохонена
Коэффициент скорости обучения
Коэффициент соседства
Количество эпох
1 этап обучения
0,1
1
10000
2 этап обучения
0,01
0
10000
При таком подходе нейронная сеть фактически начинает обучаться со второго этапа, а первый этап служит для инициализации весовой карты не малыми случайными значениями, а примерами из обучающей выборки.
Длительность первого этапа составила 10000 эпох. На каждой итерации модифицировались
веса нейрона «победителя» и 8 нейронов, которые являются его соседями из единичной окрестности. Обучение завершилось после того, как карта частот выигрышей [1] нейронов перестала заметно меняться в течение фиксированного количества эпох (приобрела стационарность).
Данные по частотам выигрышей для первого этапа приведены на рис. 2,а.
Для второго этапа были выбраны точные настройки обучения нейронной сети. Модифицировались веса только нейрона «победителя» (коэффициент соседства = 0). Так как обучающее
множество содержит сходные между собой входные векторы, то сеть должна научится активировать один и тот же нейрон для каждого из них. В этом случае веса нейрона должны получаться усреднением входных векторов, которые должны его активировать. Малое значение коэффициента скорости обучения приводит к тому, что уменьшается воздействие каждого обучающего
шага. Таким образом, окончательное значение веса будет средней величиной от входных векторов, на которых происходит обучение. Длительность второго этапа равнялась 10000 эпохам, на
последних 30 эпохах карта частот выигрышей приобрела свойство стационарности. Результаты
отработки окончательно сформированной самоорганизующейся карты Кохонена по обучающему множеству наблюдений представлены на рис. 2,б.
Частота выигрыша на
обучающих наблюдениях
0
а
10 и более
раз
б
Рис. 2. Карта частот выигрышей:
а - после первого этапа обучения, б - после второго этапа обучения
Нейросетевая диагностика двигателя по параметрам вибрации
141
Из данных, приведенных на рис. 2,б, следует, что в обучающем множестве данных нейронная сеть выделила два класса. Первый класс – верхний левый угол карты, второй – нижний правый угол карты. Так как обучение проводилось без указания целевого вектора, нельзя сразу
определить состав классов. Для этого необходимо протестировать сеть, т.е. последовательно
предъявить ей все вектора из обучающего множества, запоминая при этом нейрон какого класса
активируется. Проведенное тестирование свидетельствует о том, что в первый класс попали наблюдения, соответствующие диапазону времени работы двигателя до его остановки и проведению регламентных работ, а второй класс составляют наблюдения, соответствующие диапазону
времени после проведения регламентных работ. Это свидетельствует о том, что моменту проведения работ соответствует неоднородность по значениям параметров, подаваемых на входы
нейронной сети.
Проводился контроль работы нейронной сети. Поскольку обучающее множество трехмерно, возможно представить его в виде диаграммы в пространстве. После продолжительных экспериментов по выбору оптимального масштаба, угла поворота и наклона диаграммы получены
результаты, приведенные на рис. 3.
Объекты второго
класса
Объекты первого
класса
Рис. 3. График изменения вибраций в зоне передней подвески и частоты вращения ротора
по времени измерения их значений
Из данных, приведенных на рис. 3, следует, что при несущественном изменении частоты
вращения ротора, вибрации в зоне передней подвески выросли в 1,5-2 раза. Объектами первого
класса являются наблюдения, на которых выигрывают нейроны первого класса, объекты второго класса, соответственно, – наблюдения, которым соответствуют нейроны второго класса.
Таким образом, нейронная сеть отнесла все данные, соответствующие исходному состоянию, в первый класс, а данные после скачка по вибрациям во второй класс. Номеру измерения –
700 соответствует момент проведения на двигателе регламентных работ. Именно после этого
момента произошло существенное расслоение характеристик (рост вибраций при неизменной
М.П. Соколов
142
частоте вращения ротора). Заключение, вынесенное нейронной сетью, подтверждается графически.
Полученную модель можно использовать для вынесения решений по техническому состоянию двигателей типа Д-30ЭУ. Для этого формируется топологическая карта [1]. Поскольку
точно известно количество и состав классов, а также их смысл, то можно каждому нейрону поставить в соответствие метку класса. Первый класс объектов (исправное состояние) - нейроны
«победители» с меткой CLS1, второй класс объектов (неисправное состояние) – нейроны победители с меткой CLS2. Топологическая карта представлена на рис. 4. На вход нейронной сети
подается вектор с тремя компонентами (частота, вибрации, время), описывающими параметрическое состояние двигателя. Класс нейрона «победителя», выигравшего на этом наблюдении,
будет соответствовать классу наблюдения и состоянию двигателя. Если образец не относится
ни к одному из двух классов – выявляется его новизна.
Рис. 4. Топологическая карта
Таким образом, нейросетевые модели на основе самоорганизующихся карт Кохонена позволяют установить момент начала развития неисправности (повышенные вибрации двигателя)
на промежутке времени, достаточном для выработки мероприятий по техническому обслуживанию двигателя, направленных на предотвращение его отказа.
ЛИТЕРАТУРА
1. Нейронные сети. STATISTICA Neural Networks.-М.:Горячая линия -Телеком, 2001.
2. Kohonen Т. Self-organization and associative memory. 2d ed. New-York, Springer-Verlag, 1988.
3. Горбань А.Н. Обучение нейронных сетей. -М.: СССР-США СП "ParaGraph", 1990.
NEURAL NETWORKS DIAGNOSTIC OF THE ENGINE BY VIBRATION PARAMETERS
Sokolov M.P.
In this work was organized the diagnostics of the engine type D-30EU-2 on parameter of the vibrations by means
of using neural networks technology on example of the finding the moment of the hit in engine foreign matter. It is shown
efficiency and clarity of the using the Kohonens self-organizing maps for decision the problems of the diagnostics on complex parameter.
Сведения об авторе
Соколов Максим Павлович, 1981 г.р., окончил МГТУ ГА (2005), соискатель кафедры двигателей
летательных аппаратов МГТУ ГА, область научных интересов – диагностика авиационных двигателей
по регистрируемым параметрам.