Расчет зубчатого колеса
реклама
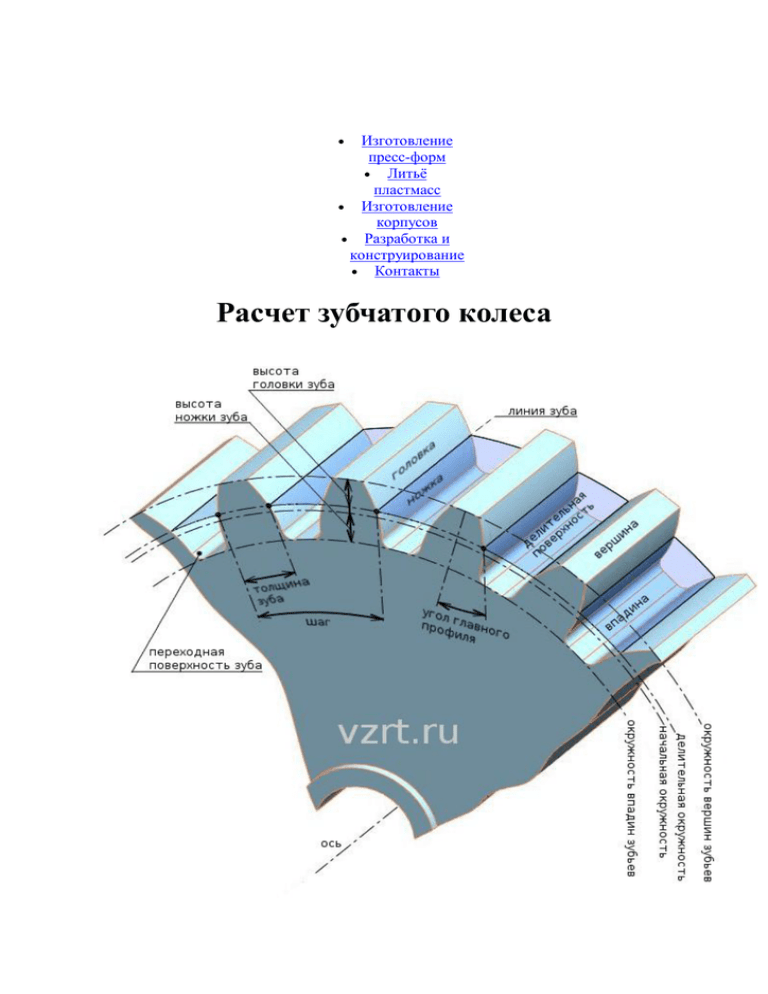
Изготовление пресс-форм Литьё пластмасс Изготовление корпусов Разработка и конструирование Контакты Расчет зубчатого колеса Первый вопрос, возникающий при построении зубчатого колеса - правильное построение профиля зуба. Поскольку наибольшее применение имеет эвольвентное зацепление, рассмотрим построение эвольвентного профиля зуба. Размеры зубьев с эвольвентным профилем определяют параметры, характеризующие положение любой точки эвольвенты. Эвольвента представляет собой развертку основной окружности диаметром Db в виде траектории точки прямой, перекатывающейся без скольжения по этой окружности. Исходными данными для расчета как эвольвенты, так и зубчатого колеса являются следующие параметры: m - Модуль - часть диаметра делительной окружности приходящаяся на один зуб. Модуль - стандартная величина и определяется по справочникам. z - количество зубьев колеса. α - угол профиля исходного контура. Угол является величиной стандартной и равной 20°. Для примера возьмем следующие данные: m = 3; z = 20; α = 20°. Делительный диаметр - это диаметр стандартного шага, модуля, и угла профиля. Он определяется по формуле: D=m·z (1), т.е. D=3·20=60 мм. Определим кривые ограничивающие эвольвенту. Этими кривыми являются: диаметр вершин зубьев и диаметр впадин зубьев. Диаметр вершин зубьев определяется по формуле: Da = D+2·m (2), т.е. Da = 60+(2·3) = 66 мм. Диаметр впадин зубьев определяется по формуле: Df = D - 2·(c + m) (3), где с - радиальный зазор пары исходных контуров. Он определяется по формуле: с = 0,25·m (4), т.е. с = 0,25·3 = 0,75. Соответственно: Df = 60 - 2·(0,75 + 3) = 52,5 мм. Диаметр основной окружности, развертка которой и будет составлять эвольвенту, определяется по формуле: Db = cos α · D (5), т.е. Db = cos 20° · 60 = 56,382 мм. Основные данные необходимые для построения эвольвенты получены. Теперь получим уравнение эвольвенты в полярных координатах. Уравнение представляется двумя параметрами: Текущим радиусом - вектором и эвольвентным углом. Определим эти параметры. Для определения эвольвентного угла (inv αt) нам необходимо задаться углом профиля зуба (αt) в торцевом сечении. В специализированной литературе можно найти таблицу дающую уже готовое значение эвольвентного угла. Но мы воспользуемся формулой: inv αt = tg αt - αt (6). Рассчитаем значение эвольвентного угла (inv αt) для угла профиля зуба (αt) в педеле от 1° до 50°. При расчете значения угла задаются в радианах. 1 радиана составляет 57,3°. Например, для 30° профиля зуба эвольвентный угол будет составлять: inv αt = (tg(30°/57,3°)-(30°/57,3°)·57,3° = 3,07922° Подобным способом рассчитывается эвольвентный угол для любого угла профиля зуба. (См. таблицу расчета). Рассчитаем теперь текущий радиус - вектор. Он рассчитывается по формуле: R = (0,5·Db) / cos αt (7). Для αt = 9°: R = (0,5·56,382)/ cos 30° = 32,551 мм. Подобным образом рассчитывается текущий радиус - вектор для любого заданного угла профиля зуба αt в диапазоне от 1° до 50°. (См. таблицу расчета). Полученные значения эвольвентного угла и текущего радиус - вектора задают координаты точек эвольвенты относительно центра строящегося колеса. Весь представленный выше расчет можно увидеть в таблице расчета, где можно рассчитать уравнение эвольвенты при своих исходных данных (заданном модуле и числе зубьев). Построение эвольвенты происходит следующим образом: Вычерчиваем основную окружность с диаметром db, откладываем эвольвентный угол и текущий радиус вектор относительно центра. Мы получаем точки, которые соединяем кривой, которая и называется эвольвентой. Построенная эвольвента представлена на рис. 1. рис.1 Эвольвента ограничивается рассчитанными ранее диаметрами вершин зубьев и впадин зубьев. Для построения всего профиля зуба необходимо знать толщину зуба по делительной окружности. Толщину зуба можно определить по формуле: S = m·((3,14/2)+(2·х·tg α)) (8), где х -коэффициент смещения зубчатого колеса. Выбирается исходя из конструктивных соображений. Для примера возьмем х = 0. Тогда: S = 3·((3,14/2) + (2·0·tg 20°)) = 4,71285 мм. Полученная толщина зуба позволяет построить законченный профиль зуба (см. рис. 2). рис.2 Таким образом построен эвольвентый профиль зуба. Простым размножением по окружности строится профиль зубчатого колеса с заданными исходными данными (см. рис. 3). рис.3 Антон Матюнин, Алексей Шаравин, 2006-2011