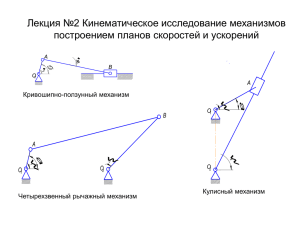
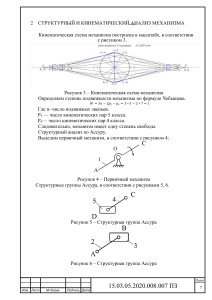
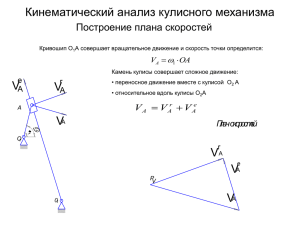
СЛОЖНОЕ ДВИЖЕНИЕ ТОЧКИ Алгоритм решения задач на

СЛОЖНОЕ ДВИЖЕНИЕ ТОЧКИ
Алгоритм решения задач на сложное движение точки
1. Указать точку и пространство, в котором рассматривается движение этой
точки ("неподвижное" пространство).
2.
Ввести подвижную систему отсчета и сделать движение точки в
"неподвижном" пространстве сложным.
3.
Указать (если это возможно) траектории точки в абсолютном,
переносном и относительном движениях.
4.
Определить искомые величины с помощью теорем сложения скоростей
и ускорений.
Пояснения
1. Если траектории точки в относительном или переносном движениях
криволинейные, то ускорение точки в каждом из этих движений надо
раскладывать на нормальное и касательное.
2. При решении векторных уравнений следует применить правило
"черточек". Две черточки под вектором означают, что известны модуль и
направление. Одна черточка под вектором указывает, что известно либо
только его направление, либо только его модуль. Уравнение решается,
если в нем не хватает двух черточек.
3. Для нахождения векторов скорости
Va
и ускорения
aa
точки в
абсолютном движении необходимо проецировать векторные уравнения,
которые входят Va и a a , на выбранные оси. Таким образом можно
определить проекции скорости
Va и ускорения a a на этой оси.
4. Решение задачи скоростей должно предшествовать решению задачи
ускорений.