39 - Квант
реклама

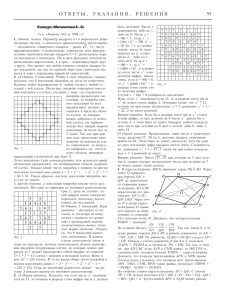
ÔÈÇÈ×ÅÑÊÈÉ + + + + + + + + + + + + 3I . + G- I .â N ? `3 I Ðèñ.3. Ñèëû, äåéñòâóþùèå íà ìîëåêóëÿðíûå çàðÿäû â ïîëÿðèçîâàííîì äèýëåêòðèêå (ìîäåëü Àíòîíà) óäàñòñÿ. Àíòîí. Íåò-íåò, ñìîòðèòå. Âîçüìåì ïðîñòåéøóþ ìîäåëü ìîëåêóëû íàøåãî íåïîëÿðíîãî äèýëåêòðèêà äâà çàðÿäà q è q, öåíòðû êîòîðûõ â íîðìàëüíîì ñîñòîÿíèè ñîâïàäàþò. Åñëè æå èõ ðàçäâèíóòü íà ðàññòîÿíèå õ («ðàñòÿíóòü» ìîëåêóëó), òî âîçíèêàåò âíóòðèìîëåêóëÿðíàÿ ñèëà Fâ x , âîçâðàùàþùàÿ çàðÿäû â èñõîäíîå ïîëîæåíèå (ðèñ.3). Ðàñòÿãèâàÿ ìîëåêóëó, ìû ñîâåðøàåì ðàáîòó ïðîòèâ ýòîé ñèëû. Ðàáîòà ýòà èäåò íà óâåëè÷åíèå ïîòåíöèàëüíîé ýíåðãèè äåôîðìàöèè ìîëåêóëû. Âîëîäÿ. Íó è êàê æå ìû íàéäåì ýòó ðàáîòó? Âåäü äëÿ ýòîãî íóæíî çíàòü Fâ x . Àíòîí. Îíà íàì íå ïîíàäîáèòñÿ! Åñëè ìû íà÷íåì ðàñòÿãèâàòü âñå ìîëåêóëû äèýëåêòðèêà â îòñóòñòâèå âíåøíåãî ýëåêòðè÷åñêîãî ïîëÿ, íàì ïðèäåòñÿ ïðåîäîëåâàòü íå òîëüêî âíóòðèìîëåêóëÿðíûå ñèëû, íî è ïîëå Es âîçíèêàþùèõ ïðè ýòîì ñâÿçàííûõ çàðÿäîâ. Ñèëà, êîòîðóþ íóæíî ïðèëîæèòü ê êàæäîé ìîëåêóëå, áóäåò ðàâíà >C >C >C F x = Fâ + qE s . ïîëÿðèçàöèþ äèýëåêòðèêà ñîçäàëî âíåøíåå ïîëå Å, òî íà êàæäûé ìîëåêóëÿðíûé çàðÿä äåéñòâóåò ýëåêòðîñòàòè÷åñêàÿ ñèëà q E − Es . Îíà äîëæíà áûòü óðàâíîâåøåíà âíóòðèìîëåêóëÿðíîé ñèëîé, ñëåäîâàòåëüíî, Fâ = = q E − E s . Òàêèì îáðàçîì, qε F x = qE = E ε −1 s (çäåñü ÿ âîñïîëüçîâàëñÿ òåì, ÷òî ðàçíîñòü E Es ðàâíà E/A). Çàìåòèì òåïåðü, ÷òî ïðè ñìåùåíèè ìîëåêóëÿðíûõ çàðÿäîâ íà õ íà ïîâåðõíîñòÿõ ïëàñòèíû âîçíèêàþò îáëàñòè íåñêîìïåíñèðîâàííîãî çàðÿäà òîëùèíîé õ. À çíà÷èò, âåëè÷èíó ñâÿçàííûõ çàðÿäîâ Qs ìû íàéäåì, åñëè óìíîæèì ìîëåêóëÿðíûé çàðÿä q íà ÷èñëî ìîëåêóë â ýòîé îáëàñòè: Qs = qnSx , ãäå n êîíöåíòðàöèÿ ìîëåêóë â äèýëåêòðèêå. Ýëåêòðè÷åñêîå ïîëå, ñîçäàâàåìîå ýòèìè ñâÿçàííûìè çàðÿäàìè, ðàâíî Q qnx Es = s = . ε0S ε0 Ïîäñòàâèâ ýòîò ðåçóëüòàò â ôîðìóëó äëÿ F(x), ïîëó÷àåì ? -I ÔÀÊÓËÜÒÀÒÈ (7) D D >C 2 > C >ε ε−q1nCε F x = x. 0 Êàê âèäèì, â ýòèõ óñëîâèÿõ êàæäàÿ ìîëåêóëà âåäåò ñåáÿ êàê ïðóæèíêà æå2 εq n . ñòêîñòüþ k = ε − 1 ε0 Âîëîäÿ. Çäîðîâî! È íèêàêîé êâàíòîâîé ìåõàíèêè. Òåïåðü, çíàÿ çàâèñèìîñòü F(õ), ìû ìîæåì íàéòè ðàáîòó, çàòðà÷åííóþ íà ðàñòÿæåíèå ìîëåêóëû. Àíòîí. Êîíå÷íî. Îñòàëîñü òîëüêî çàìåòèòü, ÷òî äëÿ ñîçäàíèÿ íà ïîâåðõíîñòÿõ ïëàñòèíû ñâÿçàííûõ çàðÿäîâ Qs êàæäóþ ìîëåêóëó íóæíî ðàñòÿíóòü íà > C x= Qs qnS . Ðàáîòà, ñîâåðøåííàÿ íàä îäíîé ìîëåêóëîé, áóäåò ðàâíà A0 = kx 2 2 2 = εQs > C 2 ε − 1 ε 0 nS 2 . ×òîáû íàéòè ïîëíóþ ðàáîòó, ò.å. ýíåðãèþ ïîëÿðèçîâàííîãî äèýëåêòðèêà, íóæíî óìíîæèòü A0 íà ÷èñëî ìîëåêóë â ïëàñòèíå: 2 Wä = ndSA0 = > εQs d C 2 ε − 1 ε0 S . Âîëîäÿ. Íî âåäü ýòî â òî÷íîñòè ðåçóëüòàò (6)! Àíòîí. Êîíå÷íî, âåäü ε 0 S d ðàâíî C0 åìêîñòè êîíäåíñàòîðà, èç êîòîðîãî ìû âûäåðãèâàëè íàøó ïëàñòèíó. Ó÷èòåëü. È òåïåðü ïîíÿòíî, ïî÷åìó èìåííî ýòîò îòâåò, à òàêæå îòâåò (1) äëÿ ýíåðãèè êîíäåíñàòîðà, ÿâëÿþòñÿ âåðíûìè, à Âîëîäèíû ðåçóëüòàòû (4) è (5) íåò. Èç ðåøåíèÿ Àíòîíà âèäíî, ãäå ó Âîëîäè âîçíèêàåò îøèáêà. Çàìåíÿÿ äèýëåêòðèê ñâÿçàííûìè çàðÿäàìè, âîçíèêàþùèìè íà åãî ïîâåðõíîñòÿõ, è âû÷èñëÿÿ ýíåðãèþ òàê, êàê åñëè áû ýòè çàðÿäû íàõîäèëèñü â âàêóóìå, ìû íå ó÷èòûâàåì ðàáîòó ïðîòèâ âíóòðèìîëåêóëÿðíûõ ñèë, çàòðà÷èâàåìóþ íà óâåëè÷åíèå ïîòåíöèàëüíîé ýíåðãèè äåôîðìàöèè ìîëåêóë Ó÷èòûâàåòñÿ òîëüêî ðàáîòà ïî ïðåîäåëåíèþ ñèë ýëåêòðè÷åñêîãî ïîëÿ, â êîòîðîì íàõîäÿòñÿ ìîëåêóëû. Èëè, äðóãèìè ñëîâàìè, òîëüêî âòîðîå ñëàãàåìîå â ôîðìóëå (7). Âîëîäÿ. Íî òîãäà, åñëè ìû îñòàâèì òîëüêî ýòî ñëàãàåìîå, ðåøåíèå Àíòîíà äîëæíî äàòü îòâåò (5). Ó÷èòåëü. Ñîâåðøåííî âåðíî. Ïîïðîáóéòå ñàìè â ýòîì óáåäèòüñÿ. Ñ äðóãîé ñòîðîíû, åñëè òó æå ñàìóþ Ôèçè÷åñêàÿ îïòèêà è äâà âåðáëþäà (Íà÷àëî ñì. íà ñ. 35) ñôåðå ìåæäó äâóìÿ çâåçäàìè ϕ , êîòîðûå ìû õîòèì ðàçðåøèòü, äîëæíî áûòü íå ìåíüøå ÷åì θ1 . (ßñíî òàêæå, ïî÷åìó ó îðëà äîëæåí áûòü áîëüøîé çðà÷îê, åñëè îí õî÷åò ñ âûñîòû ïîëåòà ðàçãëÿäåòü ìûøü íà çåìëå.) À ÷òî åñëè ïðèâèíòèòü ê òåëåñêîïó ìèêðîñêîï? Êàçàëîñü áû, åñëè êàæäûé èç ýòèõ ïðèáîðîâ óâåëè÷èâàåò â òûñÿ÷ó ðàç, òî òàêîå óñòðîéñòâî ìîãëî áû óâåëè÷èâàòü â ìèëëèîí ðàç, òàê ÷òî ìîæíî áûëî áû ðàññìàòðèâàòü êàìåøêè íà Ìàðñå? Óâû, äèôðàêöèÿ ñâåòà íà îáúåêòèâå òåëåñêîïà óæå áåçíàäåæíî èñïîðòèò äåëî, òàê ÷òî èíôîðìàöèÿ îá îáúåêòàõ áîëåå ìåëêèõ, ÷åì îïðåäåëÿåìûå óñëîâèåì Ðýëåÿ ( ), áóäåò íàâñåãäà ïîòåðÿíà. À äèôðàêöèÿ íà îáúåêòèâå ìèêðîñêîïà? Îíà âåäü òîæå ïðèâîäèò ê òîìó, ÷òî íå óäàåòñÿ ðàçðåøèòü äâå òî÷êè, åñëè ðàññòîÿíèå ìåæäó íèìè ìåíüøå äëèíû âîëíû èçëó÷åíèÿ, îñâåùàþùåãî íàáëþäàåìûé îáúåêò (íàïðèìåð, ìèêðîá). ×òî æå ïîëó÷àåòñÿ? Âûõîäèò, ýòè çàìå÷àòåëüíûå ïðèáîðû ñîçäàíû äëÿ òîãî, ÷òîáû íà èõ âõîäíûõ çðà÷êàõ ïðîèñõîäèëà äèôðàêöèÿ ñâåòà? Êîíå÷íî, íåò. Êîãäà ÷åëîâå÷åñòâî èçîáðåòàëî ýòè ïðèáîðû, îíî ñîâñåì íå äóìàëî î âîëíîâîé ïðèðîäå ñâåòà. Êàçàëîñü, êàðòèíû õîäà ëó÷åé, íàðèñîâàííûå ïî çàêîíàì ãåîìåòðè÷åñêîé îïòèêè, îòêðûâàþò íåîãðàíè÷åííûå âîçìîæíîñòè äëÿ óâåëè÷åíèÿ ìèêðîñêîïîâ è òåëåñêîïîâ ïîäáåðèòå ëèøü íóæíûå îòíîøåíèÿ ôîêóñîâ îáúåêòèâà è îêóëÿðà è ðàñïîëîæèòå èõ äîëæíûì îáðàçîì. Íî, êàê âñåãäà ñëó÷àëîñü â èñòîðèè ôèçèêè, áîëåå ðàçâèòàÿ òåîðèÿ (ôèçè÷åñêàÿ îïòèêà) óêàçàëà ïðåäåëû âîçìîæíîñòåé, ñêðûòûå îò áîëåå ïðîñòîé òåîðèè (ãåîìåòðè÷åñêîé îïòèêè). À âåðáëþäû ýòî ïðîñòî äëÿ èíòåðåñà. !'