Типовые проектные процедуры. Схема процесса

1. Типовые проектные процедуры. Схема процесса в проектировании.
Типовые проектные процедуры.
Проектная процедура называется типовой, если она предназначена для многократного применения
при проектировании многих типов объектов.
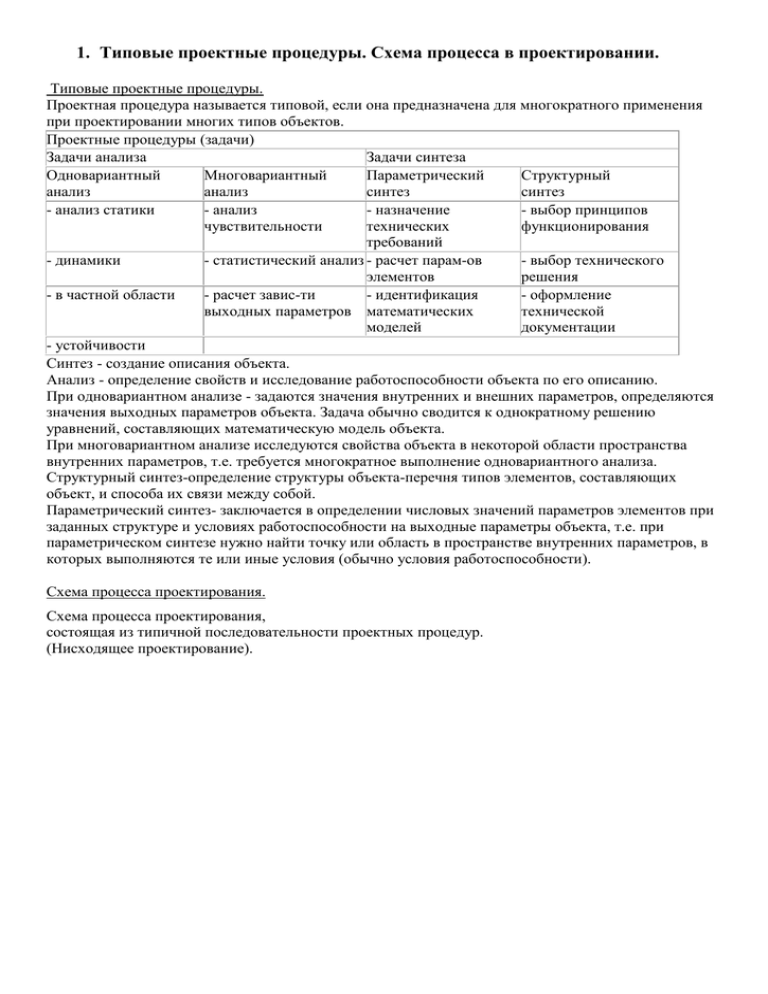
Проектные процедуры (задачи)
Задачи анализа
Задачи синтеза
Одновариантный
Многовариантный
Параметрический
Структурный
анализ
анализ
синтез
синтез
- анализ статики
- анализ
- назначение
- выбор принципов
чувствительности
технических
функционирования
требований
- динамики
- статистический анализ - расчет парам-ов
- выбор технического
элементов
решения
- в частной области
- расчет завис-ти
- идентификация
- оформление
выходных параметров математических
технической
моделей
документации
- устойчивости
Синтез - создание описания объекта.
Анализ - определение свойств и исследование работоспособности объекта по его описанию.
При одновариантном анализе - задаются значения внутренних и внешних параметров, определяются
значения выходных параметров объекта. Задача обычно сводится к однократному решению
уравнений, составляющих математическую модель объекта.
При многовариантном анализе исследуются свойства объекта в некоторой области пространства
внутренних параметров, т.е. требуется многократное выполнение одновариантного анализа.
Структурный синтез-определение структуры объекта-перечня типов элементов, составляющих
объект, и способа их связи между собой.
Параметрический синтез- заключается в определении числовых значений параметров элементов при
заданных структуре и условиях работоспособности на выходные параметры объекта, т.е. при
параметрическом синтезе нужно найти точку или область в пространстве внутренних параметров, в
которых выполняются те или иные условия (обычно условия работоспособности).
Схема процесса проектирования.
Схема процесса проектирования,
состоящая из типичной последовательности проектных процедур.
(Нисходящее проектирование).
На предыдущем уровне решались задачи k-го иерархического уровня.
Проектирование системы начинается с синтеза исходного варианта её структуры. Для оценки
варианта создаётся модель: математическая- при автоматизированном проектирование,
экспериментальная- при неавтоматизированном проектирование. Производится по исходным
параметрам анализа варианта и производится его оценка - обычно проверка условий
работоспособности из ТЗ.
Если они выполняются, то система k+1го уровня описывается в принятой форме и формулируется ТЗ
на проектирование элементов этого уровня, т.е. систем k+2го уровня. Если не выполняются, то
выбирается один из 3ёх возможных путей улучшения проекта.
Проще всего изменить числовые значения параметров элементов (выход 1), т.е. вектор Х
модифицируется.
Совокупность процедур модификации Х, анализа и оценки результатов анализа составляют
процедуру параметрического синтеза. Если модификации Х целенаправленны и подчинены
стратегии поиска наилучшего значения некоторого показателя качества, то параметрический синтез
является процедурой оптимизации.
W=k1x1+k2x2+…+knxn;
где ki- весовые коэффициенты.
Если путь 1 не приводит к результату, то используют 2ой путь, связанный с изменением структуры.
Если путь 2 не даёт результаты, то ставится вопрос о корректировке ТЗ, сформулированного на
предыдущем этапе проектирования. Это может потребовать повторения ряда процедур к-го уровня,
это обуславливает итерационный характер проектирования.
Взаимосвязь проектных процедур анализа и синтеза имеет характер вложенности.
Может оказаться, что при проектировании потребуется выполнить очень большое количество
вариантов анализа. С этим борятся тем, что сначала для отбора небольшого числа перспективных
вариантов используют упрощённые ММ, а более сложные и точные ММ для анализа небольшого
числа отобранных вариантов.
Маршрут проектирования объекта- последовательность этапов и (или) процедур, используемая
для проектирования этого объекта.
Маршрут - типовой, если он применяется при проектировании многих объектов определённого
класса.
Режимы проектирования в САПР (по степени участия человека).
- Автоматический - без вмешательства человека.
- Ручной – без ЭВМ.
Автоматизированное проектирование – невысокая автоматизация, часть процедур выполняется
вручную, часть с ЭВМ.
Диалоговый ( интерактивный) – все процедуры выполняются на ЭВМ, а человек участвует в
оперативной оценке результатов и корректирует ход проектирования.
- активный: человек- инициатор диалога, может вмешаться в любой момент.
- пассивный: человек не инициатор диалога, ждёт завершения того или иного события.
Выводы:
Проектирование – процесс получения описаний, достаточных для изготовления нового технического
объекта в заданных условиях.
Описания сложных технических объектов имеют иерархическую структуру и могут относится к
тем или иным сторонам ( группам свойств) объекта. Поэтому выделяют ряд иерархических уровней
и аспектов описаний.
Процесс проектирования делится на этапы. Этап объединяет выполнение проектных процедур по
созданию описаний, относящихся к одному аспекту или иерархическому уровню.
При выполнении проектных процедур решаются задачи синтеза и анализа описаний.
При решении задач синтеза определяются состав элементов и способ их связи между собой, а при
решении задач анализа оцениваются свойства синтезированной структуры.
Синтез называется оптимизацией, если определяются наилучшие в заданном смысле структуры и
значения параметров.
Различают:
1) параметрическую оптимизацию – расчёт оптимальных значений параметров при заданной
структуре;
2) структурную оптимизацию – задачу выбора оптимальной структуры.
2. Виды критериев оптимального проектирования.
Виды критериев оптимального проектирования.
При оптимальном проектировании их называют критериями оптимальности. Объекты
проектирования по числу критериальных показателей делятся на однокритериальные и
многокритериальные.
Пусть задача оптимального проектирования заключается в определении вектора

x  ( x1 , x 2 ,... x n ) внутренних параметров. Если в качестве целевой функции F  (x )
выбирается один наиболее важный параметр, наиболее полно характеризующий свойства
y (x )
проектируемого объекта, например yk, тогда все остальные выходные параметры j
в виде

y ( x)  TT
j где j  k относятся к ограничениям.
соответствующих условий работоспособности j
В этом случае задача оптимального проектирования является однокритериальной и заключается в
нахождении max или min целевой функции


yi ( x )  F1 ( x )  max(min)


x  x доп
Соответствующий критерий F  (x ) называется частным критерием оптимальности. Такая
задача является задачей математического программирования.
При разработке сложных систем часто нет возможности обойтись одним критерием, т.к. система
характеризуется многими параметрами, определяющими её качество и ценность. Некоторые из них
желательно максимизировать, другие минимизировать с учётом связей между ними. В этом случае
используют совокупность нескольких критериев оптимальности, задача проектирования называется
многокритериальной или задачей векторной оптимизации.
Все известные методы векторной оптимизации непосредственно ил косвенно сводят к задачам
F  (x )
скалярной оптимизации, т.е. частные критерии j
(где j=1..m - количество частных
критериев) тем или иным образом объединяются в составной критерий.
F ( x )  Ф( F1 ( x ), F2 ( x )...Fm ( x )), ,
Который потом максимизируется (или минимизируется). Следует отметить, что трудно, а иногда,
наверное, невозможно получить объективный составной критерий.
На практике составной критерий обычно образуют путём формального объединения частных
критериев, что ведёт к субъективности получаемого «оптимального» решения. Составной критерий
иногда называют обобщённым или интегральным критерием.
В зависимости от того, каким образом частные критерии обобщаются в составной различают
критерии:
1. аддитивные
2. мультипликативные
3. минимаксные (максиминные).
Кроме того, в зависимости от учёта при оптимизации статистического разброса характеристик
соответствующие критерии оптимальности называют:
1. детерминированными
2. статистическими (при учёте).
Статистические критерии более полно отражают качества объектов проектирования, но ведут к
существенным затратам времени проектирования и машинного времени.
Аддитивные и мультипликативные критерии оптимальности.
Аддитивные критерии.
В аддитивных критериях целевая функция F (x ) образуется путём сложения нормированных
значений частных критериев.


n
F ( x )   ci
i 1
Fi ( x )
н

Fi ( x )
n

  ci f i ( x )
(1)
i 1
где n- количество частных критериев,
Ci- весовой коэффициент i-го частного критерия,

Fi н ( x ) -i-ый нормирующий делитель,

f i ( x ) - нормированное значение i-го частного критерия.
Частные критерии имеют различную физическую природу, следовательно, и различную размерность.
Поэтому при образовании обобщённого критерия следует оперировать с безразмерными, т.е. с
нормированными значениями. В качестве нормирующего делителя выбирают:
1) ТТ (техническое требование) из ТЗ, заданное заказчиком.(Слабость такого подхода заключается в
предположении, что в ТЗ заданы оптимальные значения ТТ).
2) максимальные значения критериев, достигаемых в области существования проектных решений.
3) разность между MAX и MIN значениями критерия в области проектных решений.
Аддитивный критерий позволяет осуществлять компромисс, при котором улучшение значения
одного нормированного частного критерия компенсирует ухудшение другого или других.
Введение весовых коэффициентов Сi учитывает различную значимость частных критериев при
формировании аддитивного критерия. Их определение достаточно трудное и обычно сводится к
использованию формальных процедур, либо к применению экспертных оценок.
С введением обобщенного критерия исчезают проблемы, связанные с установлением взаимосвязей
между частными критериями различной размерности.
Его недостатком является то, что он не вытекает из объективной роли частных критериев в
функционировании объекта, а лишь выступает как формальный математический приём, придающий
задаче удобный для решения вид.
Другой недостаток заключается в том, что значения некоторых критериев может уменьшаться
вплоть до нуля и покрываться возрастанием других. Этот недостаток ослабляется введением
ограничений на минимальные значения частных критериев и их весовых коэффициентов Сi.
Мультипликативные критерии.
В аддитивных критериях используется принцип справедливой компенсации абсолютных значений
нормированных частных критериев.
В ряде задач целесообразным является оперирование не с абсолютными, а относительными
изменениями значений частных критериев.
Принцип справедливой относительной компенсации формулируется следующим образом:
Справедливым следует считать такой компромисс, когда суммарный уровень относительного
снижения значений одного или нескольких критериев не превышает суммарного уровня
относительного увеличения значений других критериев.
В математической форме этот принцип будет иметь вид:
n

i 1

Fi ( x )

0
Fi ( x )
,
где:
(2)

Fi ( x ) - приращение величины i-го критерия.

Fi ( x ) - первоначальная величина i-го критерия.


Fi ( x ) << Fi ( x ) , можно представить (2) как дифференциал натурального логарифма,
Полагая
тогда:
n

i 1

Fi ( x )

Fi ( x )

n
  d (ln Fi ( x ))  d (ln
i 1
n

 Fi ( x ))  0
(3)
i 1
Из выражения (3) следует, что принцип справедливой относительной компенсации приводит к
мультипликативному обобщённому критерию оптимальности.


n
F ( x )   Fi ( x )
(4)
i 1
Мультипликативный критерий образуется путём простого перемножения частных критериев в том
случае, если все они имеют одинаковую важность.
В случае неравноценности частных критериев водятся весовые коэффициенты Сi и
мультипликативный критерий принимает вид:


n
F ( x )   Fi Ci ( x )
(5)
i 1
Достоинством мультипликативного критерия является то, что при его использовании не требуется
нормировка частных критериев.
Недостаток мультипликативного критерия: критерий компенсирует недостаточную величину
одного частного критерия избыточной величиной другого и имеет тенденцию к сглаживанию
уровней частных критериев за счёт их неравнозначных значений.
Минимаксные критерии
Минимаксные и максиминные критерии используют принцип компромисса, основанный на идее
равномерности.
Сущность принципа максимина (минимакса) заключается в следующем:
Стараются найти такие значения переменных проектирования X=(x1,x2,…xm), при которых
нормированные значения всех частных критериев становятся равными между собой, т.е.:

fi ( x)  k
(6)
С учётом весовых коэффициентов важности частных критериев выражение (6) трансформируется
в соотношение вида:

ci f i ( x )  k
(7)
При большом числе частных критериев из-за сложности их взаимосвязей часто трудно добиться
выполнения соотношений (6) и (7). В этом случае принцип максимина выполняется следующим
образом:

Значения ( x ) изменяют таким образом, чтобы последовательно «подтянуть» те нормированные
критерии, численные значения которых в исходном решении оказались наименьшими.
Подтягивание «отстающего» критерия неизбежно приводит к снижению части остальных
критериев (операции ведь производятся в области компромисса).
Но при проведении ряда шагов добиваются определённой степени уравнивания противоречивых
(конфликтных) частных критериев, что является целью принципа максимина.
Формально (математически) принцип максимина можно записать:


Нужно выбрать такое ( x ) 0  ( x ) , на котором реализуется максимум из минимальных
значений частных критериев, т.е.:

0

F ( x )  max x min i { f i ( x )}
(8)
i
где i=1-n
Есть геометрическая интерпретация этого принципа, но она сложна и останавливаться на этом не
будем.
Выводы: Выбор критериев неоднозначен из-за противоречивости целей проектирования, например:
стоимость и надёжность, энергоёмкость и производительность и т.д.

а) Частный критерий F ( x ) формируется при оптимизации одного параметра при ограничениях,
наложенных на другие в ТЗ.

б) Аддитивный критерий
выбирают, если существенные значения имеют абсолютные
значения нескольких критериев.
в) Мультипликативный- если существенное значение играет изменение абсолютных значений
критериев.
г) Минимаксный - если стоит задача достижения равенства нормированных значений конфликтных
частных критериев.
3. Методы задания предпочтения на
множестве частных
критериев.
Статистический подход.
Методы задания предпочтения на множестве критериев. Метод ранжирования.
Весовые коэффициенты Ci задаются исходя из анализа современного развития отрасли, требований к
проектируемому объекту и из возможности их реализации.
Сi должны задаваться заказчиком в ТЗ на объект проектирования, но в процессе проектирования
так или иначе приходится принимать решение о предпочтении того или иного частного критерия.
Например: Если при проектировании аналогичных объектов для сферы гражданского применения на
1ое место можно поставить стоимостный критерий по важности, то для сферы военного применения
больше важна не стоимость, а надёжность объекта (автомобиль, компьютер и т.д.).
Рассмотрим получение Сi на основе экспертных оценок.
Наиболее эффективными и часто используемыми на практике оказались два метода проведения
экспертиз:
1) метод ранжирования;
2) метод приписывания баллов.
Метод ранжирования.
Пусть экспертиза проводится группой из L экспертов, специалисты в той области, где принимается
решение.

F ( x ) , i=1-n, проектируемого объекта в порядке
Каждый эксперт расставляет частные критерии i
их важности. Цифрой 1 обозначают наиболее важный частный критерий (параметр), цифрой 2
следующий по важности и т.д.
Эти ранги преобразовывают так, что ранг 1 получает оценку n, ранг 2-(n-1) и т.д. Рангу n
(k )
r
i
присваивается оценка 1. Зная преобразованный ранг
i-го критерия у k-го эксперта Ci
определяют из соотношения:
l
Ci   ri
k 1
n
(k )
l
 r
(k )
(9)
i
i 1
k 1
, i=1-n
Пример: L=3 эксперта, n=4 частных критерия.
Результат ранжирования:
i
k=1
2
1
1
2
2
3
3
4
4
Общая сумма
3
1
2
4
3

2
1
3
4
6
4
8
12
30
Из таблицы получаем веса, например, С2=4/30, С4=12/30.
Метод приписывания баллов. Статистический подход.
Метод приписывания баллов:
Эксперты оценивают важность частного критерия по шкале 0-10. При этом разрешается оценивать
важность дробными величинами или приписывать одну и туже величину из выбранной шкалы
нескольким критериям.

F ( x)
h (k )
Зная балл i i-го критерия у k-го эксперта, подсчитывают вес для i-го частного критерия i
на основе оценок k-го эксперта:
H
n
h
(k )
i
(k )
i
h
i 1
(k )
i
n
h
(k )
i
i 1
- общая сумма баллов k-эксперта.
(k )
(k )
r
H
i
i
Весовые коэффициенты Сi находят из формулы (9), заменяя в ней
на
.
Статический подход.
(k )
r
i
Индивидуальные экспертные оценки
носят на себе печать случайности, т.е. на суждение
эксперта влияют не только такие стабильные факторы, как его знания и опыт, но и множество
случайных факторов (настроение, обстановка, самочувствие и т.д.). Исходя из этого используют
статическую обработку результатов экспертных оценок, т.е. усреднение.
Среднее значение оценки для i-го критерия находят из формулы:
ri 
l
 (
l
r
(k )
k i

)
k 1
где
k
k 1
 k -коэффициент авторитета k-эксперта 0    1 .
r
Среднее значение i выражает коллективное мнение группы из L экспертов. Степень
согласованности мнений экспертов характеризуется дисперсией экспертных оценок
(среднеквадратичное отклонение) .
l
 2   ( ri( k )  ri ) 2 l
k 1
Чем меньше величина дисперсии, тем с большей надёжностью можно опираться на найденное
r
значение оценки i , т.е. надёжность экспертизы тем выше, чем меньшую долю среднего значения
составляет среднеквадратический разброс оценок  . Поэтому в качестве меры надёжности
проведённой экспертизы часто принимают коэффициент
По среднему значению оценки
Ci  ri
   ri
, который называют вариацией.
ri определяют весовой коэффициент:
n
r
i
i 1
, i=1-n
В заключении отметим, что существуют и другие формальные процедуры выработки предпочтения
на множестве частных критериев, но мы на них останавливаться не будем.
Вообще, под этим вопросом скрывается очень много методов и теорий (например, теория игр,
расписаний и т.д.).
4. Методы
трехмерного
моделирования.
Представление
трехмерных
объектов в АвтоКад.
Методы трехмерного моделирования. Логические операции
Различают 3 основных метода:
1. Каркасное (проволочное) моделирование.
2. Поверхностное (полигональное) моделирование .
3. Твердотельное (объемное или сплошное).
1. Каркасные модели задаются координатами вершин и соединяющих их ребрами. Эта модель
проста, но с ее помощью можно представить в пространстве только ограниченный класс объектов,
в которых грани, заключенные меду ребрами, преимущественно являются плоскостям.
Широко используются для имитации движения инструмента выполняющего несложные операции
обработки детали по 2,5 или 3 осям. Понятие 2,5 – мерного объекта относятся к относительно
простым объектам имеющим постоянное поперечное сечение вдоль третьей координаты (глубины
объекта). Например, цилиндр 3-тья координата, параллелепипед и др.
Каркасные модели – модели самого низкого уровня, имеющие серьезные ограничения, связанные с
недостатком информации о гранях и невозможностью выделить внешнюю и внутреннюю область
изображения твердого объемного тела.
С их помощью не всегда можно получить правильные изображения а также автоматически
анализировать процессы удаления невидимых линий и получения различных сечений.
К другим ограничениям относятся:
а) невозможность обнаружения взаимного влияния компонентов
б) отсутствие возможности получение типовых изображений , т.к. затенению подвергаются грани (а
их нет), а не ребра и ряд других.
2. Поверхностные модели задаются с помощью точек линий и поверхностей. Эта модель более
высокого уровня, чем каркасная.
Поверхностные модели имеют следующие преимущества по сравнению с каркасным
а) способность распознавать и изображать сложные криволинейные грани
б) способность получения тоновых 3-х мерных изображений (т.к. грани распознаваемы).
в) способность распознавания особых построений на поверхностях, например, отверстия,
пересечения и сопряжения поверхностей
г) способность с помощью полигональной модели (аппроксимация поверхностей многогранником)
описать любую поверхность технического объекта.
д) способность выполнения над полигональными моделями ГО. логических операций объединения
вычитания, пересечения.
Типы поверхностей.
1.Базовые геометрические поверхности.
К ним относят поверхности, получаемые разверткой на заказанное расстояние в 3-х мерном
пространстве отрезка, дуги, круги. Таким образом можно получить соответственно плоские
поверхности, криволинейные, цилиндрические, конические, например:
С помощью развертки плоской области можно сформировать 3-х мерный объект:
2. Поверности вращения - получаются вращением плоской фигуры грани вокруг определенной оси
(круговая развертка).
Следует отметить, что полученные 3х – мерные объекты представляются как поверхности,
соединенные друг с другом в пространстве и ограничивающие «пустой» объем, т.е. не создается
твердое тело, а генерируются только поверхность.
3. Поверхности пересечений и сопряжении.
Построение плавного сопряжения одной поверхности с другой по особым кривым в 3х – мерном
пространстве, строящихся методом сплайн-интерполяции.
Например: Сопряжение параллелепипеда и цилиндра.
4. Аналитические поверхности. Каждая поверхность определяется одним математическим
уравнением с неизвестными X,Y,Z.
Например: уравнение сферы X2+Y2+Z2=a2.
5. Скульптурные поверхности (известны также как поверхность «свободных форм» или
«произвольные» поверхности) нельзя описать одним математическим уравнением. Эти поверхности
создаются путем построения сплайнов продольных образующих кривых между точками,
определенными в 3-х мерном пространстве
Например: точки в пространстве, заданные поперечным сечениями.
6. Составные поверхности. Составная поверхность (обычно криволинейная) может быть полностью
определена сеткой четырехугольных кусков (участков, ограниченных продольными и поперечными
линиями на поверхности).
Каждый кусок имеет форму топологического прямоугольника (его стороны не обязательно прямые
и попарно перпендикулярны). Такие поверхности называют многоугольными сетями, плотность
которой задается двухпараметрическим массивом вершин М*N.
Координаты вершин описываются в пространстве х, у, z.
Многоугольные сети используются в Автокаде. С помощью их можно построить практически
любую поверхность, а также легко создавать частные варианты поверхностей, например, цилиндр,
конус, сфера , тор и т.д.
Недостатки поверхностного моделирования:
Несмотря на многие достоинства, недостатки поверхностного моделирования могут быть устранены
только с помощью твердотельного моделирования. Основные недостатки возникают из-за “пустого”
объема внутри поверхностей:
а) неоднозначность при моделировании реального твердого тела (разрезов, сечений)
б) сложность процедур удаления скрытых линий и отображения внутренних областей. Например,
при отсечении некоторой части поверхности “пустой” объем становится “прозрачным” и становится
видна другая поверхность.
в) неточность получения массо-инерционных характеристик.
3.Твердотельные модели формируются из элементарных объектов (базисных тел) с использованием
логических операций объединения, вычитания, пересечения.
Твердотельное моделирование обеспечивает полное однозначное описание 3-х мерной
геометрической формы.
Это наиболее мощный из 3-х методов 3-х мерного моделирования.
Преимущество твердотельных моделей:
а) полное определение объемной формы с возможностью разграничения внешний и внутренней
областей объекта, что необходимо для обнаружения нежелательных взаимовлияний компонентов;
б) обеспечение автоматического удаления скрытых линий;
в) автоматическое построение 3-х мерных разрезов компонентов, что особенно важно при анализе
сложных сборочных изделий;
г) возможность присвоения объектом физических и материальных свойств, обеспечение расчета
весовых и прочностных характеристик с отображением результатов, возможность применения МКЭ;
д) геометрическое описание объектов может напрямую использоваться для проектирования
технологической оснастки;
е) повышение эффективности имитации динамики механизмов, движения инструментов и роботов.
Базисные тела называют твердотельными примитивами. Твердотельные примитивы могут быть
созданы с помощью развертки 2-у мерных областей в 3-х мерном пространстве, с помощью
круговой развертки (тела вращения) как при поверхностном моделировании. Но, в данном случае,
образуется существенно «твердый объем» (описан весь объем. а не поверхности), а не пустое
пространство, ограниченное несколькими поверхностями.
Геометрическое описание твердотельного объекта хранится в базе данных ( в Автокаде), а на экране
мониторе может быть построено одно из его следующих представлений:
пространственный линейный каркас;
очерковая линия и линии пересечения поверхностей;
многоугольная сеть, аппроксимирующая поверхность.
Объемные тела, образованные из базисных тел с использованием логических операций
объединения, вычитание и пересечение называются составными геометрическими объектами.
Приведем графическую интерпретацию логических операций:
Теория множеств
Объединение (U)
Разность (-)
Пересечение(П)
Пример твёрдых тел.
Методы создания моделей ГО и ГИ.
Можно выделить два основных вида ГО:
1.
постоянный – с постоянными размерами и геометрической формой, например, ГИ условных
графических обозначений радио изделий электрических схем, стандартное изделие с постоянными
размерами (кирпич).
2.
параметрически заданный – с переменными размерами и геометрической формой, например,
типовые конструкции в виде ферм, колонн, несущие конструкции – балки, унифицированные
конструкции – подшипники и т.д.
Постоянные ГО – могут быть легко сформированы с использованием графических редакторов,
например, AutoCAD
Параметрически заданные ГО могут быть созданы двумя принципиально различными методами:
вариантным и генерирующим.
Вариантный метод основан на том, что для определенного класса объектов выявляется модельпредставитель, с помощью которой можно получить все геометрические формы этого класса
объектов. Представители класса объектов называют типовой моделью (или комплексной моделью),
а полученные из нее формы – вариантами (исполнителями). Вариант объект определяется
заданными параметрами, обнуление которых приводит к исключению составных элементов ГО. В
простейшем случае изменяются только размеры, а конструкция отдельных вариантов семейства
объектов остается неизменной.
Областями применения являются проектирование отдельных деталей (пружин), комплексных узлов (
подшипников), готовых объектов (трансформаторов) и т.д.
Затраты на описание типовой модели относительно велики по сравнению с затратами на получение
вариантов, поэтому многие системы используют принцип вложенности моделей: один раз описанные
типовые модели используются для описания других типовых моделей в качестве макрокоманд (или
макросов).
Генерирующий метод основан на разделен ГО на элементы и создании новых ГО из имеющихся
элементов САПР, работающие по генерирующему методу, обладают высокой гибкостью и пригодны
для решения различных задач. Опыт показывает, что большинство новых конструкторских
разработок создаются путем ранее неиспользовавшегося сочетания элементов, давно известных как
по принципу функционирования, так и по исполнению.
Подводя черту, можно сказать, что с конкретными примерами геометрического моделирования вы
знакомитесь при работе с Автокадом, имеющими богатейшие возможности моделирования.